Gọi nửa quãng đường là S

\(t_1\) là thời gian đi hết nửa quãng đường đầu

\(t_1=\dfrac{s}{12}\)

\(t_2\) là thời gian đi hết nửa quãng đường sau

\(t_2=\dfrac{S}{v_2}\)

\(v_{tb}=\dfrac{S+S}{t_1+t_2}=\dfrac{2S}{\dfrac{S}{12}+\dfrac{S}{v_2}}=8\) 

\(\Leftrightarrow\dfrac{2S}{\dfrac{S\left(12+v_2\right)}{12v_2}}=8\Leftrightarrow\dfrac{24v_2}{12+v_2}=8\Rightarrow v_2=6\) km/h

tính x,y,z 

x=3y=27z và 2x-3y+4z=48

\(\Leftrightarrow\dfrac{1}{a}=\dfrac{2b-3}{4}\Rightarrow a=\dfrac{4}{2b-3}\left(b\ne\dfrac{3}{2}\right)\) (1)

\(a\in Z\Rightarrow\left(2b-3\right)=\left\{-4;-2;-1;1;2;4\right\}\)

\(\Rightarrow b=\left\{-\dfrac{1}{2};\dfrac{1}{2};1;2;\dfrac{5}{2};\dfrac{7}{2}\right\}\) Do \(b\in Z\Rightarrow b=\left\{1;2\right\}\)

Thay vào (1) \(\Rightarrow a=\left\{-4;4\right\}\)

Bài 6

Gọi x (phần) là số phần thưởng nhiều nhất cô giáo có thể chia (x ∈ ℕ*)

⇒ x = ƯCLN(128; 48; 142)

Ta có:

128 = 2⁷

48 = 2⁴.3

142 = 2.71

⇒ x = ƯCLN(128; 48; 142) = 2 

Mỗi phần thưởng có:

128 : 2 = 64 (quyển vở)

48 : 2 = 24 (bút chì)

142 : 2 = 71 (tập giấy)

Châu Á là châu lục lớn nhất thể giới nằm trong lục địa Á-Âu 

Có diện tích khoảng: \(44580000km^2\)

Châu Á là lục địa lớn nhất trên Trái đất, với diện tích khoảng 44,58 triệu km². Nó chiếm khoảng 30% tổng diện tích của toàn bộ bề mặt đất liền và có hơn 4,5 tỷ người sinh sống trên đây, tương đương với hơn 60% dân số thế giới. Châu Á có địa hình đa dạng, từ các dãy núi cao như dãy Himalaya và dãy Ural, đến các vùng đồng bằng và sa mạc rộng lớn như sa mạc Gobi và sa mạc Thar. Với sự đa dạng văn hóa, lịch sử và địa lý, Châu Á là một lục địa đáng khám phá và có sự ảnh hưởng lớn đến toàn cầu.

A B C D E F G H

a/

Ta có

EF//AC (gt); GH//AC (gt) => EF//GH (1)

Xét tg ABC có

AE=BE (gt)

EF//AC (gt)

=> BF=CF (trong tg đường thẳng đi qua trung điểm của 1 cạnh ; // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

=> EF là đường trung bình của tg ABC \(\Rightarrow EF=\dfrac{AC}{2}\) (2)

Xét tg BCD chứng minh tương tự => CG=DG

Xét tg ACD chứng minh tương tự => AH=DH

=> GH là đường trung bình của tg ACD \(\Rightarrow GH=\dfrac{AC}{2}\) (3)

Từ (2) và (3) => EF=GH (4)

Từ (1) và (4) => EFGH là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

EFGH là hình chữ nhật \(\Rightarrow\widehat{EFG}=90^o\Rightarrow EF\perp FG\)

Mà FG//BD (gt)

\(\Rightarrow EF\perp BD\) mà EF//AC (gt) \(\Rightarrow AC\perp BD\)

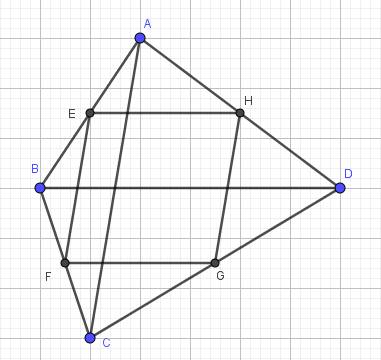
a) \(\Delta ABC\) có:

E là trung điểm của AB (gt)

EF // AC (gt)

\(\Rightarrow\) F là trung điểm của BC

\(\Rightarrow\) EF là đường trung bình của \(\Delta ABC\)

\(\Rightarrow EF=\dfrac{AC}{2}\) (1)

\(\Delta BCD\) có:

F là trung điểm của BC (cmt)

FG // BD (gt)

\(\Rightarrow\) G là trung điểm của CD

\(\Delta ACD\) có:

G là trung điểm của CD (cmt)

GH // AC (gt)

\(\Rightarrow\) H là trung điểm của AD

\(\Rightarrow\) GH là đường trung bình của \(\Delta ACD\)

\(\Rightarrow\) \(GH=\dfrac{AC}{2}\) (2)

Từ (1) và (2) \(\Rightarrow EF=GH\)

Do EF // AC (gt)

GH // AC (gt)

\(\Rightarrow\) EF // GH

Tứ giác EFGH có:

EF // GH (cmt)

EF = GH (cmt)

\(\Rightarrow EFGH\) là hình bình hành

b) Để EFGH là hình chữ nhật thì \(EF\perp FG\)

Lại có:

EF // AC (gt)

FG // BD (gt)

\(\Rightarrow AC\perp BD\)

Vậy \(AC\perp BD\) thì EFGH là hình chữ nhật

A B C M N D

a/

Xét tứ giác BMCD có

NB=NC (gt)

ND=NM (gt)

=> BMCD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

b/

Để BMCD là hình thoi \(\Rightarrow MD\perp BC\) (Hình thoi có 2 đường chéo vuông góc) (1)

Ta có

MA=MC (gt)

NB=NC (gt)

=> MN là đường trung bình của tg ABC => MN//AB => MD//AB (2)

Từ (1) và (2) \(\Rightarrow AB\perp BC\)

Để BMCD là hình thoi => tg ABC là tg vuông tại B

a) Tứ giác BMCD có:

N là trung điểm của BC (gt)

N là trung điểm của DM (gt)

\(\Rightarrow\) BMCD là hình bình hành

b) Để BMCD là hình thoi thì \(BC\perp DM\)

Ta có:

M là trung điểm của AC (gt)

N là trung điểm của BC (gt)

\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MN\) // \(AB\)

\(\Rightarrow DM\) // \(AB\)

Mà \(DM\perp BC\)

\(\Rightarrow BC\perp AB\)

Vậy để BMCD là hình thoi thì \(\Delta ABC\) vuông tại B

M N Q P A I K

MN//PQ (cạnh đối hbh) => MI//KQ

Ta có

\(MI=\dfrac{MN}{2};KQ=\dfrac{PQ}{2}\) Mà MN=PQ (cạnh đối hbh) => MI=KQ

=> MIKQ là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

Ta có

MA=MQ (gt) (1)

\(MN=2MQ\left(gt\right)\Rightarrow MQ=\dfrac{MN}{2}\) (2)

Ta có

\(MI=\dfrac{MN}{2}\) (3)

Từ (1) (2) (3) \(\Rightarrow MA=MI=\dfrac{MN}{2}\) => tg AMI cân tại M

Ta có

\(\widehat{AMI}=\widehat{AMP}-\widehat{M}=180^o-120^o=60^o\)

Xét tg AMI có

\(\widehat{MAI}+\widehat{MIA}+\widehat{AMI}=180^o\)

\(\Rightarrow\widehat{MAI}+\widehat{MIA}=180^o-\widehat{AMI}=180^o-60^o=120^o\)

Mà \(\widehat{MAI}=\widehat{MIA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\dfrac{120^o}{2}=60^o\)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\widehat{AMI}=60^o\Rightarrow\Delta AMI\) là tg đều

c/

Xét hbh MNPQ có

MQ//NP => MA//NP

MA=MQ (gt); MQ=NP (cạnh đối hbh)

=> MA=NP

=> APMN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

\(MI=AI=\dfrac{MN}{2}\)  (cạnh tg đều)

\(NI=\dfrac{MN}{2}\)

\(\Rightarrow AI=NI=\dfrac{MN}{2}\) => tg AIN cân tại I

Ta có \(\widehat{AIN}=\widehat{MIN}-\widehat{AIM}=180^o-60^o=120^o\)

Xét tg cân AIN có

\(\widehat{AIN}+\widehat{IAN}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{IAN}+\widehat{INA}=180^o-\widehat{AIN}=180^o-120^o=60^o\)

Mà \(\widehat{IAN}=\widehat{INA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{IAN}=\widehat{INA}=\dfrac{60^o}{2}=30^o\)

Xét tg AMN có

\(\widehat{MAN}+\widehat{AMI}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{MAN}=180^o-\widehat{AMI}-\widehat{INA}=180^o-60^o-30^o=90^o\)

=> APMN là hình chữ nhật (hình bình hành có 1 góc vuông là HCN

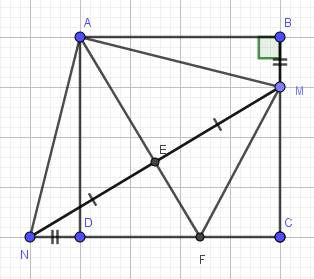
a) Do ABCD là hình vuông (gt)

\(\Rightarrow AB=AD\)

\(\widehat{ABM}=\widehat{ADN}=90^0\)

Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:

\(AB=AD\left(cmt\right)\)

\(BM=DN\left(gt\right)\)

\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)

\(\Rightarrow AM=AN\) (hai cạnh tương ứng)

\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)

Ta có:

\(\widehat{BAM}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)

\(\Rightarrow\widehat{MAN}=90^0\)

\(\Delta AMN\) có:

\(AM=AN\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) cân tại A

Mà \(\widehat{MAN}=90^0\left(cmt\right)\)

\(\Rightarrow\Delta AMN\) vuông cân tại A

b) Do \(\Delta AMN\) cân tại A

E là trung điểm của MN

\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)

\(\Rightarrow AE\perp MN\)

\(\Rightarrow EF\perp MN\)

Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:

\(EM=EN\left(gt\right)\)

\(EF\) là cạnh chung

\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)

\(\Rightarrow FM=FN\) (hai cạnh tương ứng)

Xét \(\Delta FAN\) và \(\Delta FAM\) có:

\(FA\) là cạnh chung

\(FN=FM\left(cmt\right)\)

\(AN=AM\left(cmt\right)\)

\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)