`@` `\text {Ans}`

`\downarrow`

`16,`

`@` Các cặp góc đồng vị:

`+`\(\widehat {M_4}\) và \(\widehat {N_4}\)

`+`\(\widehat {M_1}\) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_2}\)

`+`\(\widehat {M_3}\) và \(\widehat {N_3}\)

`@` Các cặp góc sole trong:

`+`\(\widehat {M_3} \) và \(\widehat {N_1}\)

`+`\(\widehat {M_2}\) và \(\widehat {N_4}\) 

`b,`

Ta có: \(\widehat {M_3} = \widehat {M_1} (\text {đối đỉnh})\)

`=>`\(\widehat {M_1}=50^0\)

\(\widehat {M_3}+\widehat {M_2}=180^0 (\text {kề bù})\)

`=>`\(50^0+\widehat {M_2}=180^0\)

`=>`\(\widehat {M_2}=180^0-50^0=130^0\)

\(\widehat {M_2}=\widehat {M_4} (\text {2 góc đối đỉnh})\)

`=>`\(\widehat {M_4} = 130^0\)

Vì \(\widehat {M_3}\) và \(\widehat {N_1}\) là `2` góc sole trong

`=>`\(\widehat {M_3}=\widehat {N_1}=50^0\)

\(\widehat {M_3}=\widehat {N_3}=50^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_2}=130^0 (\text {2 góc đồng vị})\)

\(\widehat {M_2}=\widehat {N_4}=130^0 (\text {2 góc slt})\)

`17,`

Vì \(\widehat {A_1}\) và \(\widehat {A_2}\) là `2` góc kề bù

`=>`\(\widehat {A_1}+\widehat {A_2}=180^0\)

\(3\widehat {A_1}=2\widehat {A_2}\) (gt)

`=>`\(\widehat{A_1}=\dfrac{2}{3}\cdot\widehat{A_2}\)

Thay \(\widehat{A_1}=\dfrac{2}{3}\widehat{A_2}\)

\(\dfrac{2}{3}\cdot\widehat{A_2}+\widehat{A_2}=180^0\)

`=>`\(\widehat{A_2}\left(\dfrac{2}{3}+1\right)=180^0\)

`=>`\(\widehat{A_2}\cdot\dfrac{5}{3}=180^0\)

`=>`\(\widehat{A_2}=180^0\div\dfrac{5}{3}\)

`=>`\(\widehat{A_2}=108^0\)

Vậy, số đo \(\widehat{A_2}=108^0\)

\(\widehat {A_1}+\widehat {A_2}=180^0 (\text {kề bù})\)

`=>`\(\widehat{A_1}+108^0=180^0\)

`=>`\(\widehat{A_1}=72^0\)

\(\widehat {A_1}=\widehat {A_3}=72^0 (\text {đối đỉnh})\)

\(\widehat {A_2}=\widehat {A_4}=108^0 (\text {đối đỉnh})\)

`@` Số đo các góc của đỉnh B:

`+`\(\widehat {A_4}=\widehat {B_4}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_2}=\widehat {B_2}=108^0 (\text {đồng vị})\)

`+`\(\widehat {A_3}=\widehat {B_1}=72^0 (\text {sole trong})\)

`+`\(\widehat {A_3}=\widehat {B_3}=72^0 (\text {đồng vị})\)

Trong 21 ngày đội trồng được :

\(21:7\times1000=3000\) cây 

Trong 21 ngày đội trồng được :

$21:7\times 1000=3000$ cây 

Ta có sơ đồ:

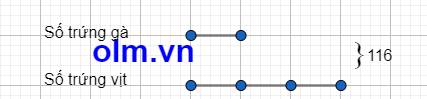
Theo sơ đồ ta có số trứng gà là: 116:(1+3) = 29 (quả)

Số trứng vịt là: 116 - 29 = 87 (quả)

Đáp số: trứng gà 29 quả

             trứng vịt 87 quả 

Ta có sơ đồ:

Theo sơ đồ ta có số trứng gà là: 116:(1+3) = 29 (quả)

Số trứng vịt là: 116 - 29 = 87 (quả)

Đáp số: trứng gà 29 quả

Ta có thể sử dụng công thức Newton về đa thức để giải bài toán này. Đặt đa thức $P(x) = (x-a)(x-b)(x-c) = x^3 - (a+b+c)x^2 + (ab+bc+ca)x - abc$.

Do $a+b+c=0$, nên $P(x) = x^3 - 3kx - abc$ với $k = \frac{ab+bc+ca}{a+b+c}$.

Ta có thể tính được $a^2+b^2+c^2 = -2(ab+bc+ca)$.

Đặt $S_n = a^n + b^n + c^n$. Ta có thể suy ra các công thức sau:

$S_1 = 0$

$S_2 = a^2 + b^2 + c^2 = -2(ab+bc+ca)$

$S_3 = 3abc$

$S_4 = (a^2+b^2+c^2)^2 - 2(a^2b^2+b^2c^2+c^2a^2) = 2(ab+bc+ca)^2 - 3abc(a+b+c)$

$S_5 = 5(ab+bc+ca)(a^2+b^2+c^2) - 5abc(a+b+c)$

$S_6 = (a^2+b^2+c^2)^3 - 3(a^2+b^2+c^2)(a^2b^2+b^2c^2+c^2a^2) + 2(a^2b^2c^2)$

$S_7 = 7(ab+bc+ca)(a^2+b^2+c^2)^2 - 14abc(a^2+b^2+c^2) + 7a^2b^2c^2$

Từ đó, ta có thể tính được $S_1, S_2, S_3, S_4, S_5, S_6$ dựa trên các giá trị đã biết.

Đặt $T_n = a^n+b^n+c^n - S_n$. Ta có thể suy ra các công thức sau:

$T_1 = 0$

$T_2 = 2S_2$

$T_3 = 3S_3$

$T_4 = 2S_2^2 - 4S_4$

$T_5 = 5S_2S_3 - 5S_5$

$T_6 = 2S_2S_4 + 3S_3^2 - 6S_6$

$T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7$

Do $S_1=S_3=0$, nên $T_1=T_3=0$.

Từ $a+b+c=0$, ta có $a^2+b^2+c^2 = -2(ab+bc+ca)$. Do đó, $S_2 = 2(ab+bc+ca)$ và $S_4 = 2(ab+bc+ca)^2 - 3abc(a+b+c) = 2(ab+bc+ca)^2$.

Từ $a^7+b^7+c^7=0$, ta có $T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7 = 7S_2S_5 - 14S_4S_3 + 7S_7 = 7S_7$.

Từ $T_7 = 7S_7$, ta có $S_7 = \frac{T_7}{7} = 0$.

Do đó, $T_6 = 2S_2S_4 + 3S_3^2 - 6S_6 = 2(2(ab+bc+ca))(2(ab+bc+ca)^2) + 3(abc)^2 - 6S_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$.

Từ $T_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$, ta có $S_6 = \frac{1}{6}(12(ab+bc+ca)^2 + 3(abc

Giải

Vì a + b + c = 0 nên a + b = -c

Ta có:

\(a^7+b^7=\left(a+b\right)\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =-c\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =c\left(-a^6+a^5b-a^4b^2+a^3b^3-a^2b^4+ab^5-b^6\right)\\ =c\left[-\left(a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6\right)+\left(7a^5b+14a^4b^2+21a^3b^3+14a^2b^4+7ab^5\right)\right]\\ =c\left[-\left(a+b\right)^6+7ab\left(a^4+2a^3b+3a^2b^2+2ab^3+b^4\right)\right]\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)^2+2ab\left(a^2+b^2\right)+3a^2b^2-2a^2b^2\right]\right\}\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =c\left\{-c^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =-c^7+7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\\ \Rightarrow a^7+b^7+c^7=7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\Rightarrow7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]=0\)TH1: \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2=0\)

Vì \(a^2,b^2,\left(a+b\right)^2,a^2b^2\ge0\) nên \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\ge0\)

Dấu "=" xảy ra khi và chỉ khi a = b = 0

Mà a + b + c = 0 nên suy ra c = 0

Vậy \(a^{2023}+b^{2023}+c^{2023}=0\)

TH2: abc = 0

Vì abc = 0 nên sẽ có ít nhất một trong ba số a, b, c = 0

Vì a, b, c có vai trò như nhau nên không mất tính tổng quát, giả sử \(c=0\)

Mà a + b + c = 0 nên a + b =0 hay a = -b

\(\Rightarrow a^{2023}+b^{2023}+c^{2023}=0\)

Kết luận: \(a^{2023}+b^{2023}+c^{2023}=0\)

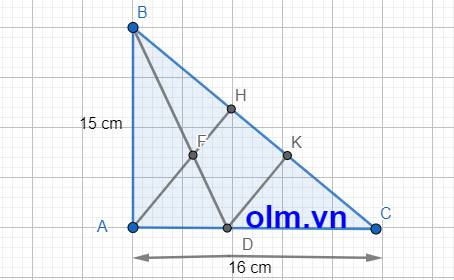
a, Xét \(\Delta\)BAH và \(\Delta\)BCA có: \(\widehat{ABC}\)  chung; \(\widehat{AHB}\) = \(\widehat{BAC}\) = 90⁰

⇒\(\Delta\)BAH \(\sim\)\(\Delta\)BCA (g-g)

⇒\(\dfrac{BA}{BC}=\dfrac{AH}{CA}=\dfrac{BH}{BA}\)

b, Theo pytago ta có: BC² = AB² + AC² = 15²+16² = 481 (cm²)

⇒ BC = \(\sqrt{481}\) cm

Kẻ đường cao DK vuông góc với BC cắt BC tại K 

DA = DK ( vì mọi điểm trên tia phân giác thì cách đều hai cạnh còn lại)

Vì \(\Delta\)ABD và \(\Delta\)BCD có đường cao bằng nhau nên tỉ số diện tich hai tam giác bằng tỉ số hai cạnh đáy và bằng:

\(\dfrac{AB}{BC}\) = \(\dfrac{15}{\sqrt{481}}\)  

Tương tự ta có tỉ số diện tích hai tam giác, tam giác ABD và tam giác BCD bằng:

\(\dfrac{AD}{DC}\) ⇒ \(\dfrac{AD}{DC}\) = \(\dfrac{15}{\sqrt{481}}\) ⇒ \(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) = \(\dfrac{AD+DC}{15+\sqrt{481}}\) = \(\dfrac{16}{15+\sqrt{481}}\) 

AD = \(\dfrac{16}{15+\sqrt{481}}\)\(\times\)15 = \(\dfrac{240}{15+\sqrt{481}}\) = \(\dfrac{15}{16}\)(\(\sqrt{481}\) - 15)

DC = \(\dfrac{16}{15+\sqrt{481}}\) \(\times\) \(\sqrt{481}\) = \(\dfrac{1}{16}\)(481 - 15\(\sqrt{481}\))

Đổi 120 000 l = 120 m³ 

Chiều cao của hồ nước cũng chính là độ sâu của hồ và bằng:

120 : ( 8 \(\times\) 3) = 5 (m)

Kết luận chiều sâu của hồ nước là 5m 

Đổi \(120000l=120m^3\)

Ta có : \(V=d.r.h\Rightarrow h=\dfrac{V}{d.r}=\dfrac{120}{8.3}=\dfrac{120}{24}=5\left(m\right)\)

Vậy độ sâu của hồ nước là 5m.

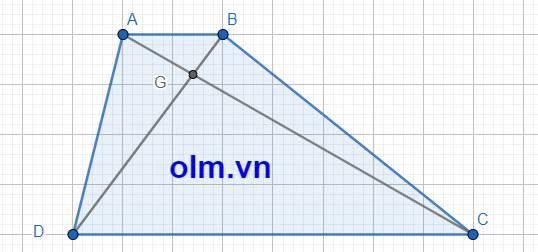
S_ABD  = S_{ABC (}vì hai tam giác có hai chiều cao bằng nhau và chung đáy AB)

⇒ S_ABG + S_ADG = S_ABG + S_BCG ⇒ S_ADG = S_BCG = 179,2 cm²

Vì \(\Delta\)ABG và \(\Delta\)BCG có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích \(\Delta\)ABG và \(\Delta\)BGC là tỉ số hai cạnh đáy:

\(\dfrac{AG}{GC}\) = \(\dfrac{44,8}{179,2}\) = \(\dfrac{1}{4}\)

Vì \(\Delta\)ADG và \(\Delta\)DCG có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích \(\Delta\)ADG và \(\Delta\)DCG là tỉ số hai cạnh đáy:

\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)

⇒S_DCG = S_ADG : \(\dfrac{1}{4}\) = 179,2 : \(\dfrac{1}{4}\) = 716,8 (cm²)

Diện tích của hình thang ABCD là:

44,8 + 179,2 + 179,2 + 716,8 = 1120 (cm²)

Đáp số: 1120 cm²

\(x+\dfrac{5}{2}=-\dfrac{1}{7}\)

\(\Rightarrow x=-\dfrac{1}{7}-\dfrac{5}{2}\)

\(\Rightarrow x=-\dfrac{2}{14}-\dfrac{35}{14}\)

\(\Rightarrow x=\dfrac{-2-35}{14}\)

\(\Rightarrow x=\dfrac{-37}{14}\)

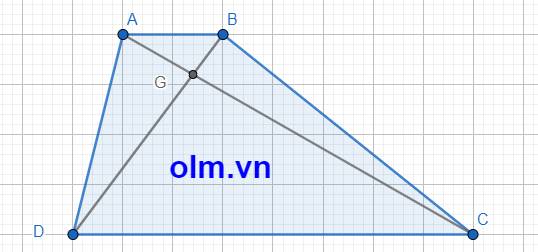
S_ABD = S_ABC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy AB)

⇒ S_ABG + S_ADG = S_ABG + S_BCG ⇒ S_ADG = S_BGC = 170,8 cm²

\(\Delta\)ABG và \(\Delta\)BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:

\(\dfrac{AG}{GC}\) = \(\dfrac{42,7}{170,8}\) = \(\dfrac{1}{4}\)

\(\Delta\)AGD và \(\Delta\)DGC có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và băng

\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)

⇒S_DGC = S_{AGD : \(\dfrac{1}{4}\)}

Diện tích tam giác DGC là: 170,8 : \(\dfrac{1}{4}\) = 683,2 (cm²)

Diện tích hình thang ABCD là:

42,7 + 170,8 + 170,8 + 683,2  = 1067,5 (cm²)

Đáp số: 1067,5 cm²

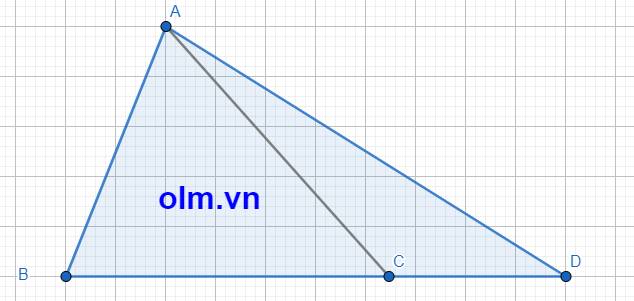
BD = BC + CD = BC + \(\dfrac{7}{9}\)BC = \(\dfrac{16}{9}\)BC

S_ABD = \(\dfrac{16}{9}\) S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BD và BD = \(\dfrac{16}{9}\)BC)

Diện tích tam giác ABD là: 279 \(\times\) \(\dfrac{16}{9}\) = 496 (cm²)

Đáp số: 496 cm²