Gọi chiều rộng hình chữ nhật là x(m)

(Điều kiện: x>0)

Chiều dài hình chữ nhật là x+7(m)

Diện tích là 120m² nên ta có: x(x+7)=120

=>\(x^2+7x=120\)

=>\(x^2+7x-120=0\)

=>(x+15)(x-8)=0

=>\(\left[{}\begin{matrix}x+15=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-15\left(loại\right)\\x=8\left(nhận\right)\end{matrix}\right.\)

Vậy: Chiều rộng là 8m

Chiều dài là 8+7=15m

Ta gọi chiều rộng là x, chiều dài là x+7.

Ta có phương trình: x(x + 7) = 120

Ta giải phương trình:

• x² + 7x = 120
• x² + 7x - 120 = 0
• Phân tích thành nhân tử: (x - 8)(x + 15) = 0
• ⇒ x - 8 = 0 hoặc x + 15 = 0
• ⇒ x = 8 hoặc x = -15.

Ta kết luận:

• Vì chiều rộng không thể âm nên ta loại bỏ nghiệm x = -15.
• Vậy chiều rộng của hình chữ nhật là 8m.
• Chiều dài của hình chữ nhật là 8 + 7 = 15m.

Vậy chiều dài là 15 m và chiều rộng là 8 m.

a: Ta có: ΔOBD cân tại O

mà OA là đường cao

nên OA là phân giác của góc BOD

Xét ΔOBA và ΔODA có

OB=OD

\(\widehat{BOA}=\widehat{DOA}\)

OA chung

Do đó: ΔOBA=ΔODA

=>\(\widehat{OBA}=\widehat{ODA}\)

=>\(\widehat{ODA}=90^0\)

=>AD là tiếp tuyến của (O)

Xét (O) có

ΔBDE nội tiếp

BE là đường kính

Do đó: ΔBDE vuông tại D

=>BD\(\perp\)DE

mà BD\(\perp\)OA

nên OA//DE

b: Xét (O) có

ΔBFE nội tiếp

BE là đường kính

Do đó: ΔBFE vuông tại F

=>BF\(\perp\)AE tại F

Xét ΔBEA vuông tại B có BF là đường cao

nên \(AF\cdot AE=AB^2\left(1\right)\)

Xét ΔABO vuông tại B có BC là đường cao

nên \(AC\cdot AO=AB^2\left(2\right)\)

Từ (1),(2) suy ra \(AF\cdot AE=AC\cdot AO\)

a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1),(2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H và H là trung điểm của AB

Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

Xét tứ giác OHBI có \(\widehat{OHB}=\widehat{OIB}=\widehat{HBI}=90^0\)

nên OHBI là hình chữ nhật

b: ΔOBD cân tại O

mà OI là đường cao

nên OI là phân giác của góc BOD

Xét ΔODK và ΔOBK có

OD=OB

\(\widehat{DOK}=\widehat{BOK}\)

OK chung

Do đó: ΔODK=ΔOBK

=>\(\widehat{ODK}=\widehat{OBK}\)

=>\(\widehat{ODK}=90^0\)

=>KD là tiếp tuyến của (O)

c: Xét ΔOBM vuông tại B có BH là đường cao

nên \(OH\cdot OM=OB^2\)

=>\(OH=\dfrac{R^2}{2R}=\dfrac{R}{2}\)

ΔOHB vuông tại H

=>\(OH^2+BH^2=OB^2\)

=>\(BH=\sqrt{R^2-\left(\dfrac{R}{2}\right)^2}=\dfrac{R\sqrt{3}}{2}\)

mà BH=OI

nên \(OI=\dfrac{R\sqrt{3}}{2}\)

ΔOBD cân tại O

mà OI là đường cao

nên I là trung điểm của BD

Ta có: OH=BI

mà BI=ID(I là trung điểm của BD)

nên OH=DI

=>DI=R/2

Xét ΔODK vuông tại D có DI là đường cao

nên \(\dfrac{1}{DI^2}=\dfrac{1}{DO^2}+\dfrac{1}{DK^2}\)

=>\(\dfrac{1}{DK^2}=\dfrac{1}{\left(\dfrac{R}{2}\right)^2}-\dfrac{1}{R^2}=\dfrac{1}{\dfrac{R^2}{4}}-\dfrac{1}{R^2}=\dfrac{3}{R^2}\)

=>\(DK=\dfrac{R\sqrt{3}}{3}\)

ΔADK vuông tại D

=>\(DA^2+DK^2=AK^2\)

=>\(AK=\sqrt{\left(\dfrac{R\sqrt{3}}{3}\right)^2+\left(2R\right)^2}=\dfrac{R\sqrt{39}}{3}\)

Chu vi tam giác ADK là:

AD+DK+AK

\(=2R+\dfrac{R\sqrt{3}}{3}+\dfrac{R\sqrt{39}}{3}=R\left(2+\dfrac{\sqrt{3}+\sqrt{39}}{3}\right)\)

Gọi giá niêm yết của một cái bàn là là x(nghìn đồng)

(Điều kiện: x>0)

Giá niêm yết của một cái quạt điện là 850-x(nghìn đồng)

Giá tiền thực tế của cái bàn là là: \(x\left(1-10\%\right)=0,9x\left(nghìnđồng\right)\)

Giá tiền thực tế của cái quạt điện là:

\(\left(850-x\right)\left(1-20\%\right)=0,8\left(850-x\right)=680-0,8x\left(nghìnđồng\right)\)

Tổng số tiền phải trả là:

850-125=725(nghìn đồng)

=>0,9x+680-0,8x=725

=>0,1x=725-680=45

=>x=450(nhận)

Vậy: Số tiền thực tế anh Bình phải trả cho cái bàn là là: \(450\cdot0,9=405\) nghìn đồng

Số tiền thực tế anh Bình phải trả cho cái quạt điện là:

\(680-0,8\cdot450=320\left(nghìnđồng\right)\)

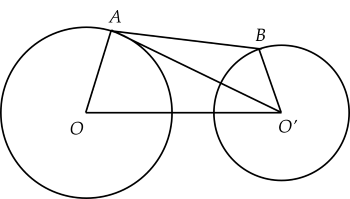
Xét \(\Delta ABO':\)

\(AB\ge O'A-O'B\left(1\right)\)

Xét \(\Delta OAO':\)

\(O'A\ge O'O-OA\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow AB\ge O'O-OA-O'B=950-500-300=150\left(m\right)\)

Dấu '=' xảy ra khi \(4\) điểm \(O;A;B;O'\) thẳng hàng

\(\Rightarrow\) Xây cầu có chiều dài là \(150\left(m\right)\) trên đoạn nối 2 tâm cầu 2 hòn đảo (O'O) thì cây cầu sẽ ngắn nhất.

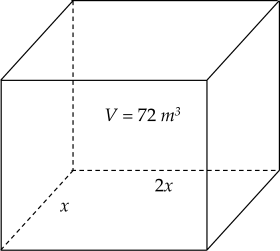
Diện tích đáy bể là: \(2x^2\) `(m^2)`

Chiều cao bể là: \(\dfrac{72}{2x^2}=\dfrac{36}{x^2}\left(m^2\right)\)

Diện tích xung quanh bể là: \(\left(2x+x\right).2.\dfrac{36}{x^2}=\dfrac{216}{x}\left(m^2\right)\)

Diện tích cần xây là:

\(2x^2+\dfrac{216}{x}=2\left(x^2+\dfrac{54}{x}+\dfrac{54}{x}\right)\ge2.3\sqrt[3]{x^2.\dfrac{54}{x}.\dfrac{54}{x}}=54\sqrt[3]{4}\left(m^2\right)\)

Dấu "=" xảy ra khi \(x^2=\dfrac{54}{x}\Rightarrow x=\sqrt[3]{54}=3,78\left(m\right)\)

a: Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại H và H là trung điểm của BC

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\)

b: ΔODE cân tại O

mà OI là đường trung tuyến

nên OI\(\perp\)DE tại I

Xét ΔFOA có

AI,OB là các đường cao

AI cắt OB tại G

Do đó: G là trực tâm của ΔFOA

=>FG\(\perp\)OA 

c: Gọi H là trung điểm của FA

ΔFIA vuông tại I

mà IH là đường trung tuyến

nên IH=HA=HF

=>H là tâm đường tròn ngoại tiếp ΔFIA

ΔOIG vuông tại I

mà IQ là đường trung tuyến

nên QI=QG

=>ΔQIG cân tại Q

\(\widehat{HIQ}=\widehat{HIG}+\widehat{QIG}=\widehat{HAI}+\widehat{QGI}\)

mà \(\widehat{QGI}=\widehat{BGA}\)(hai góc đối đỉnh)

nên \(\widehat{HIQ}=\widehat{BGA}+\widehat{BAG}=90^0\)

=>HI\(\perp\)IQ

=>IQ là tiếp tuyến của đường tròn ngoại tiếp ΔFIA

2\(x^2\) + 5\(x\) + 3 = 0

a - b + c = 2 - 5 + 3 = 0

Vậy pt có hai nghiệm phân biệt là:

\(x_1\) = -1; \(x_2\) = - \(\dfrac{c}{a}\) = \(\dfrac{-3}{2}\)

Vậy S= {- \(\dfrac{3}{2}\); -1}

Ta có: \(2x^2+5x+3=0\)

=>\(2x^2+2x+3x+3=0\)

=>2x(x+1)+3(x+1)=0

=>(x+1)(2x+3)=0

=>\(\left[{}\begin{matrix}x+1=0\\2x+3=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-1\\2x=-3\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)

a: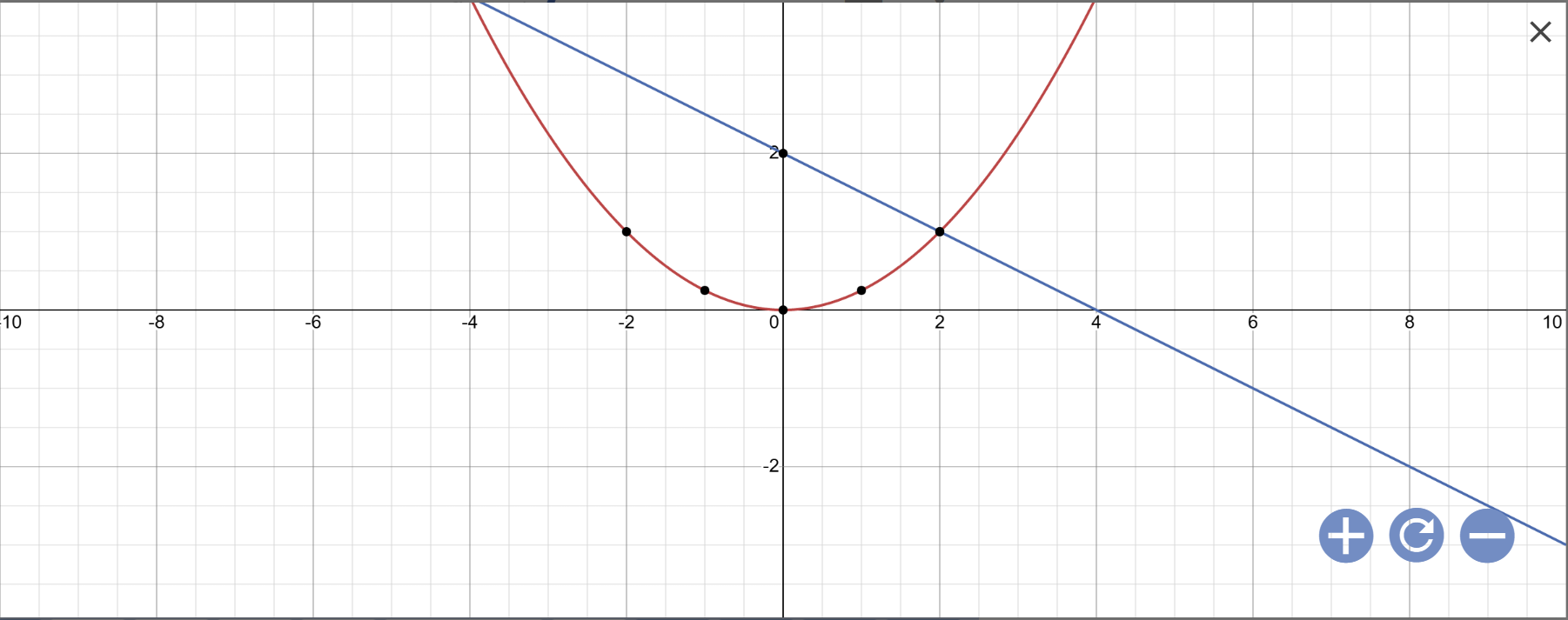 

b: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x+2\)

=>\(x^2=-2x+8\)

=>\(x^2+2x-8=0\)

=>(x+4)(x-2)=0

=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)

Khi x=-4 thì \(y=-\dfrac{1}{2}\cdot\left(-4\right)+2=2+2=4\)

Khi x=2 thì \(y=-\dfrac{1}{2}\cdot2+2=-1+2=1\)

Vậy: Tọa độ giao điểm của (P) và (d) là A(-4;4); B(2;1)