Vì khi cha sinh con là 24 tuổi nên cha hơn con 24 tuổi(khúc này bạn không hiểu thì có thể tìm hiểu thêm)

Cha:↔↔↔↔↔

24 tuổi

Con:↔

(↔ là phần)

Hiệu số phần bằng nhau là:

5-1=4(phần)

Giá trị mỗi phần là:

24:4=6

Số tuổi của cha vào năm nay là:

6x5=30(tuổi)

Đáp số:30 tuổi.

Bn có thể làm gộp bước 2 và 3.

Chúc học tốt!❤

Do con sinh ra lúc cha 24 tuổi nên hiệu số tuổi hai cha con là 24

Tuổi cha năm nay là: 

`24 : (5-1) xx 5 = 30` (tuổi)

Đáp số: 30 tuổi

Ta có: `16 = 1 + 15 = 2+ 14 = 3 + 13 = 4 + 12 = 5 + 11 = 6 + 10 = 7 + 9 = 8 + 8`

Mà 8/8 = 1 nên loại 8+8

Các phân số bé hơn 1 mà tổng tử và mẫu bằng 16 là: 

`1/15; 2/14; 3/13; 4/12; 5/11; 6/10 ; 7/9`

Có 7 phân số thỏa mãn

Các trường hợp thỏa mãn:

Tử số = 1: Mẫu số = 15. Ta có phân số 1/15.

Tử số = 2: Mẫu số = 14. Ta có phân số 2/14.

Tử số = 3: Mẫu số = 13. Ta có phân số 3/13.

Tử số = 4: Mẫu số = 12. Ta có phân số 4/12.

Tử số = 5: Mẫu số = 11. Ta có phân số 5/11.

Tử số = 6: Mẫu số = 10. Ta có phân số 6/10.

Tử số = 7: Mẫu số = 9. Ta có phân số 7/9.

Vậy, có tổng cộng 7 phân số thỏa mãn yêu cầu đề bài.

Trả lời nhanh nha!!!👉👈🙏🙏

a) 12 567 + 3 243 = 15810

b) 154 908 - 54 908 = 100 000

c) 56 x 94 = 5264

d) 345 : 24 = 14, 375

a, Một lớp học có số bạn nữ là:
\(40\times20\%=8\) ( bạn)
( Kiểm tra lại ý b ạ)
 

a) Số bạn nữ là:

40 : 100 x 20% = 8 (bạn nữ)

b) Bạn nam chiếm số phần trăm học sinh trong lớp là :

100% - 20% = 80%

Số bạn nam là:

40 : 100 x 80% = 32 (bạn nam)

Em xem lại đề bài chỗ chiều rộng nhé

Giải:

(3n + 2) ⋮ (1 - n) (đk (n ≠ 1)

[-3(1- n) + 5] ⋮ (1 - n)

5 ⋮ (1 - n)

(1 - n) ∈ Ư(5) = {-5; -1; 1; 5}

Lập bảng giá trị ta có:

Theo bảng trên ta có n ∈ {6; 2; 0; - 4}

Vậy n ∈ {-4; 0; 2; 6}

\(\left\{{}\begin{matrix}x_1=3y_1\\2y_1-x_1=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=3y_1\\2y_1-3y_1=-7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-y_1=-7\\x_1=3y_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_1=7\\x_1=3\cdot7=21\end{matrix}\right.\)

x và y là hai đại lượng tỉ lệ thuận

=>\(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)

=>\(\dfrac{21}{45}=\dfrac{7}{y_2}\)

=>\(\dfrac{7}{y_2}=\dfrac{7}{15}\)

=>\(y_2=15\)

a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC\)

Xét ΔCHA vuông tại H và ΔCAB vuông tại A có

\(\widehat{HCA}\) chung

Do đó ΔCHA~ΔCAB

=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)

=>\(CA^2=CH\cdot CB\)

b: ΔCHA~ΔCAB

=>\(\dfrac{CA}{CB}=\dfrac{AH}{AB}\)

=>\(AB\cdot AC=AH\cdot BC\)

c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HBA}\right)\)

Do đó: ΔHAB~ΔHCA

=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)

=>\(HA^2=HB\cdot HC\)

d: \(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{AB^2+AC^2}{\left(AB\cdot AC\right)^2}=\dfrac{BC^2}{\left(BC\cdot AH\right)^2}=\dfrac{1}{AH^2}\)

e: \(AH^2=HB\cdot HC=4\cdot9=36\)

=>\(AH=\sqrt{36}=6\left(cm\right)\)

BC=BH+CH=4+9=13(cm)

ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot6\cdot13=39\left(cm^2\right)\)

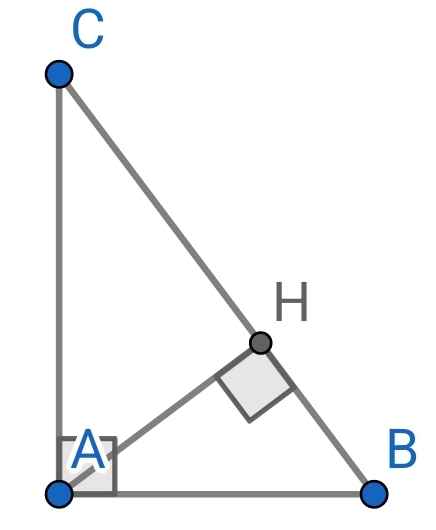
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:

∠B chung

⇒ ∆ABC ∽ ∆HBA (g-g)

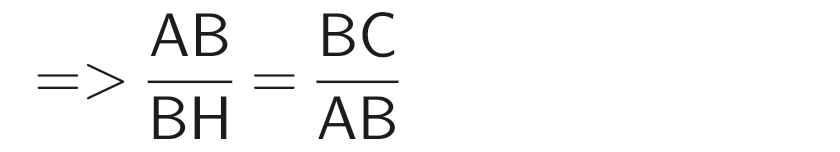
⇒ AB² = BH.BC

Xét hai tam giác vuông: ∆ABC và ∆HAC có:

∠C chung

⇒ ∆ABC ∽ ∆HAC (g-g)

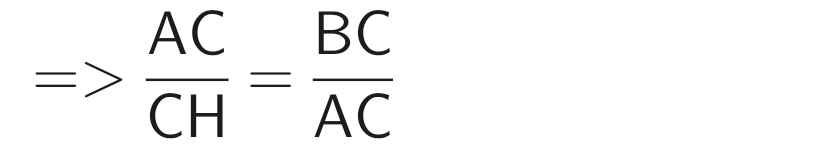
⇒ AC² = CH.BC

b) Do ∆ABC ∽ ∆HBA (cmt)

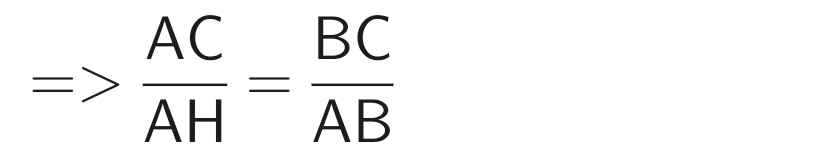
⇒ AH.BC = AB.AC

c) Do ∆ABC ∽ ∆HBA (cmt)

∆ABC ∽ ∆HAC (cmt)

⇒ ∆HBA ∽ ∆HAC

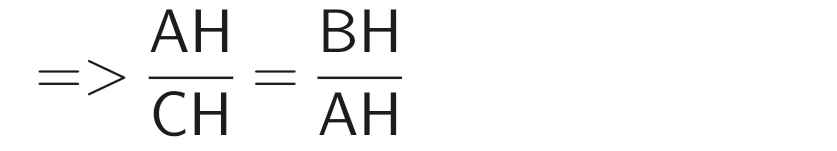
⇒ AH² = BH.CH

d) Do AH.BC = AB.AC (cmt)

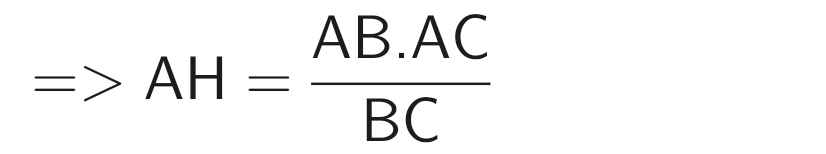
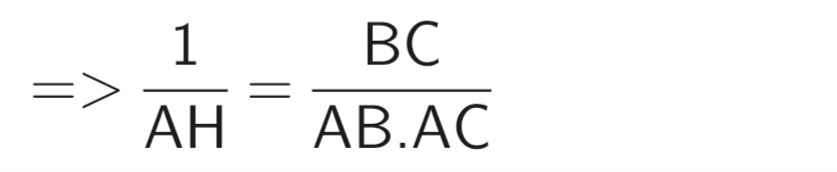
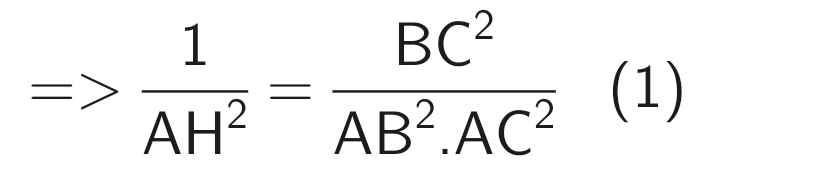
Do ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

Thế BC² = AB² + AC² vào (1), ta được:

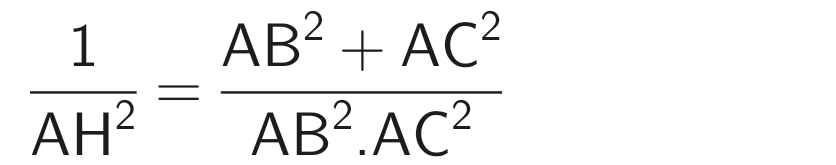
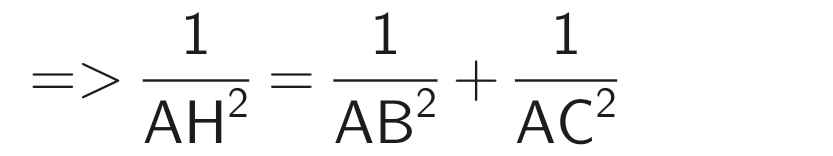
e) Ta có:

BC = BH + CH = 4 + 9 = 13

Lại có:

AH² = BH.CH (cmt)

⇒ AH² = 4.9 = 36

⇒ AH = 6

Diện tích ∆ABC

S = 6 . 13 : 2 = 39 (đvdt)

\(2024A=\dfrac{2024^{2025}+2024}{2024^{2025}+1}=1+\dfrac{2023}{2024^{2025}+1}\)

\(2024B=\dfrac{2024^{2026}-2\cdot2024}{2024^{2026}-2}=1-\dfrac{2\cdot2023}{2024^{2026}-2}\)

mà \(\dfrac{2023}{2024^{2025}+1}>-\dfrac{2\cdot2023}{2024^{2026}-2}\)

nên 2024A>2024B

=>A>B

Số gói ở mỗi thùng nhiều hơn số gói ở mỗi hộp là:

100 : 5 = 20 (gói)

Hiệu số phần bằng nhau:

2 - 1 = 1 (phần)

Số gói ở mỗi thùng:

20 : 1 × 2 = 40 (gói)

Số gói ở mỗi hộp:

40 : 2 = 20 (gói)

Số gói buổi sáng bán được:

40 × 5 = 200 (gói)

Số gói buổi chiều bán được:

20 × 5 = 100 (gói)

Đây là toán nâng cao chuyên đề hiệu tỉ, ẩn tỉ. Cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

Giải:

Vì số gói mỗi ở thùng buổi sáng nhiều gấp đôi số gói ở hộp buổi chiều nên tỉ số số gói buổi chiều so với số gói buổi sáng là:

1 : 2 = \(\frac12\)

Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có:

Số gói bán buổi sáng là:

100 : (2 - 1) x 2 = 200 (gói)

Số gói bán buổi chiều là:

200 - 100 = 100(gói)

Đáp số: Số gói bán buổi sáng là: 200 gói

Số gói bán buổi chiều là: 100 gói