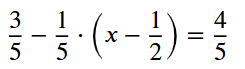\(\dfrac{3}{5}-\dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{3}{5}-\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=-\dfrac{1}{5}\\ x-\dfrac{1}{2}=-\dfrac{1}{5}:\dfrac{1}{5}\\ x-\dfrac{1}{2}=-1\\ x=-1+\dfrac{1}{2}\\ x=-\dfrac{1}{2}\)

Giải:

Số có hai chữ số có dạng: \(\overline{ab}\)

Viết thêm chữ số 0 vào giữa hai chữ số của số đó ta được số mới là: \(\overline{a0b}\)

Theo bài ra ta có:

\(\overline{a0b}\) = 6 x \(\overline{ab}\)

100a + b = 60a + b

100a + b - 60a - 6b = 0

(100a - 60a) - (6b - b) = 0

40a - 5b = 0

8a - b = 0

8a = b

b ≤ 9 ⇒ 8a ≤ 9 ⇒ a ≤ 9 : 8 ⇒ a < 2 ⇒ a = 0; 1

Vì a không thể bằng không nên a = 1, b = 8a = 8.1 = 8

Vậy số cần tìm là 18

Phân số chỉ số phần cửa hàng bán được số gạo trong ngày thứ 3 là :
                  3/7x25%=3/28

Phân số chỉ số gạo cửa hàng còn lại sau khi bán ngày thứ nhất và thứ 3 là :

                     1-(3/7+3/28)=13/28

Số gạo ban đầu của cửa hàng là:

                       26:13/38=56(tấn)

                                         Đáp số:56 tấn gạo          

                                        Bài giải:

a/Sau khi bán ngày thứ nhất cửa hàng còn lại :
       1 - 3/7 = 4/7 ( số gạo )
Ngày thứ ba bán được 25% ngày thứ nhất có nghĩa là số gạo ngày thứ ba bán bằng 1/4 số gạo ngày thứ nhất đã bán.
Vậy ngày thứ ba bán được :
      3/7 x 1/4 = 3/28 (số gạo)

Số gạo bán ngày thứ hai bằng: 1-3/7 3/28=13/28(số gạo)

Ban đầu cửa hàng có số gạo là: 26:13/28=56 (tấn)

b,Số gạo bán được trong ngày 3 là: 56x3/28=6(tấn)

c,số gạo cửa hàng bán được trong ngày 1 chiếm: 24:56x100%=42,857% (số gạo của cửa hàng)

                                           Đáp số: a/ 56 tấn;

                                                        b/ 6 tấn;

                                                         c/ 42,857%.

a. Khi gieo con xúc xắc số, các kết quả số chấm xuất hiện có thể là: 1; 2; 3; 4; 5; 6 chấm

Vậy các kết quả có thể để sự kiện số chấm xuất hiện là số nguyên tố xảy ra là: 

2, 3, 5 chấm

b. Do 5 khác 6 nên nếu số chấm xuất hiện là 5 thì sự kiện số chấm xuất hiện không phải là 6 có xảy ra.

Các kết quả có thể xảy ra của sự kiện "Số chấm xuất hiện là số nguyên tố"

=>Các kết quả có thể xảy ra là 2;3;5

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Hay

x + x = x

2x = x

2x - x = 0

X = 0

Vậy x = 0

x + x = x 2x = x

2x - x = 0

X = 0

Vậy x = 0

Olm chào em, em muốn sửa bài thì em chỉ cần bấm vào nút luyện tập lại. Sau đó em làm lại bài và cố gắng làm thật tốt là được, em nhé. Cảm ơn em đã đồng hành cùng Olm. chúc em học tập hiệu quả và vui vẻ cùng Olm.

Hay

13/5-(-2/15)=13/5+2/15=39/15+2/15=41/15

__________________________________

M O A B

Giải;

a) Độ dài đoạn thẳng AB là:

7 - 3,5 = 3,5 (cm)

b)Độ dài đoạn thẳng AM là:

3,5 + 2 = 5,5 (cm)

Vì : 5,5 < 7

Nên: Độ dài đoạn thẳng AM bé hơn độ dài đoạn thẳng OB

c) Trên hình vẽ có 6 đoạn thẳng: OM; OA; AB; AM; OB; BM.

Để giải bài toán này, chúng ta sẽ làm từng câu một:

a) Tính độ dài đoạn thẳng AB

Đoạn thẳng \(A B\) là đoạn nối giữa hai điểm \(A\) và \(B\) trên cùng một tia \(O X\).

• \(O A = 3 , 5 \textrm{ } \text{cm}\) và \(O B = 7 \textrm{ } \text{cm}\).
• Vì \(A\) và \(B\) nằm trên cùng một tia \(O X\) và \(O B > O A\), nên \(A B = O B - O A\).

Cách tính:

\(A B = O B - O A = 7 \textrm{ } \text{cm} - 3 , 5 \textrm{ } \text{cm} = 3 , 5 \textrm{ } \text{cm}\)

Kết luận: Đoạn thẳng \(A B\) có độ dài là 3,5 cm.

b) Trên tia đối của tia OX, lấy điểm M sao cho OM bằng 2cm. So sánh độ dài các đoạn thẳng AM và OB

• \(O M = 2 \textrm{ } \text{cm}\) là đoạn thẳng trên tia đối của tia \(O X\), tức là đoạn \(O M\) nằm ngược chiều với tia \(O X\).
• Đoạn \(A M\) sẽ là tổng của độ dài \(O A\) và \(O M\) (vì \(M\) nằm trên tia đối của tia \(O X\)):

\(A M = O A + O M = 3 , 5 \textrm{ } \text{cm} + 2 \textrm{ } \text{cm} = 5 , 5 \textrm{ } \text{cm}\)

• So sánh độ dài các đoạn thẳng:
• • Đoạn thẳng \(A M = 5 , 5 \textrm{ } \text{cm}\).
  • Đoạn thẳng \(O B = 7 \textrm{ } \text{cm}\).

Kết luận: Đoạn thẳng \(O B\) dài hơn đoạn thẳng \(A M\), vì \(7 \textrm{ } \text{cm} > 5 , 5 \textrm{ } \text{cm}\).

c) Trên hình vẽ, ta có tất cả mấy đoạn thẳng? Kể tên các đoạn thẳng đó

Từ các thông tin trên, chúng ta có các đoạn thẳng sau:

1. \(O A\) = 3,5 cm (Đoạn thẳng từ \(O\) đến \(A\)).
2. \(O B\) = 7 cm (Đoạn thẳng từ \(O\) đến \(B\)).
3. \(A B\) = 3,5 cm (Đoạn thẳng từ \(A\) đến \(B\)).
4. \(O M\) = 2 cm (Đoạn thẳng từ \(O\) đến \(M\) trên tia đối của tia \(O X\)).
5. \(A M\) = 5,5 cm (Đoạn thẳng từ \(A\) đến \(M\)).

Kết luận: Ta có 5 đoạn thẳng: \(O A\), \(O B\), \(A B\), \(O M\), và \(A M\).

Hy vọng giải đáp này giúp bạn hiểu rõ bài toán!

Đừng lo, mình sẽ giúp bạn giải bài này một cách rõ ràng nhé!

Đầu tiên, ta thấy biểu thức SS là một tổng các phân số có mẫu số dạng tích của hai số liên tiếp. Mẫu số của mỗi phân số có dạng n(n+2)n(n+2), với nn chạy từ 3 đến 2021 và tăng dần thêm 2 (tức là n=3,5,7,…,2021n = 3, 5, 7, \dots, 2021).

Phân tích biểu thức:

Phân số 5n(n+2)\frac{5}{n(n+2)} có thể được tách thành:

Trong đó AA và BB là các hằng số cần tìm.

Giải phương trình:

So sánh hệ số:

• A+B=0A + B = 0
• 2A=52A = 5

Từ đó, ta tìm được:

Thay vào biểu thức ban đầu:

Vậy tổng SS trở thành một tổng dạng telesope (các số hạng triệt tiêu lẫn nhau):

Tính tổng:

Các số hạng giữa triệt tiêu, còn lại:

Kết quả:

Vậy đáp số cuối cùng là S=50506069S = \frac{5050}{6069}.

1. Tách phân số:

• Ta thấy mỗi số hạng của S đều có dạng 5/n(n+2).
• Ta có thể tách 5/n(n+2) như sau:
• • 5/n(n+2) = 5/2 * (1/n - 1/(n+2))

2. Áp dụng công thức:

• Áp dụng công thức trên cho từng số hạng của S, ta được:
• • S = 5/2 * (1/3 - 1/5) + 5/2 * (1/5 - 1/7) + 5/2 * (1/7 - 1/9) + ... + 5/2 * (1/2019 - 1/2021) + 5/2 * (1/2021 - 1/2023)

3. Rút gọn:

• Đặt 5/2 làm thừa số chung, ta có:
• • S = 5/2 * (1/3 - 1/5 + 1/5 - 1/7 + 1/7 - 1/9 + ... + 1/2019 - 1/2021 + 1/2021 - 1/2023)
• Ta thấy các số hạng -1/5 và 1/5, -1/7 và 1/7, ..., -1/2021 và 1/2021 triệt tiêu lẫn nhau.
• Vậy, S = 5/2 * (1/3 - 1/2023)

4. Tính toán:

• S = 5/2 * (2020/6069)
• S = 5050/6069

Kết luận:

• S = 5050/6069