
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Trên tia Ox, ta có: OB<OA
nên B nằm giữa O và A
=>OB+BA=OA
=>BA+3=6
=>BA=3(cm)
b: Vì B nằm giữa O và A
mà BO=BA(=3cm)
nên B là trung điểm của OA
c; I là trung điểm của AB
=>\(BI=AI=\dfrac{AB}{2}=1,5\left(cm\right)\)
Vì AI<AO
nên I nằm giữa A và O
=>AI+OI=AO
=>OI+1,5=6
=>OI=4,5(cm)
a) Vì B nằm giữa O và A nên
OB+BA=OA
Thay số: 3+BA=6
BA= 6-3
BA = 3 ( cm)
Vậy độ dài đoạn thẳng AB là 3cm
b)Vì B nằm giữa O và A
OB=BA=3cm
Vậy O là trung điểm của đoạn thẳng AB
c) Vì I là trung điểm của BA nên
BI= BA:2
Thay số: BI= 3:2
BI= 1,5
Vậy độ đoạn thẳng OI là 1,5

\(\dfrac{x-1}{3}=\dfrac{5}{y+2}\)
=>(x-1)(y+2)=3*5=15
=>\(\left(x-1;y+2\right)\in\left\{\left(1;15\right);\left(15;1\right);\left(-1;-15\right);\left(-15;-1\right);\left(3;5\right);\left(5;3\right);\left(-3;-5\right);\left(-5;-3\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(2;13\right);\left(16;-1\right);\left(0;-17\right);\left(-14;-3\right);\left(4;3\right);\left(6;1\right);\left(-2;-7\right);\left(-4;-5\right)\right\}\)
\(\dfrac{x-1}{3}\) = \(\dfrac{5}{y+2}\) (\(x;y\) \(\in\) Z)
\(x\) = \(\dfrac{5}{y+2}\) x 3 + 1
\(x\) = \(\dfrac{15}{y+2}\) + 1
\(x\in\)Z ⇔ y + 2 \(\in\) Ư(15) = {-15; - 5; -3; -1; 1; 3; 5; 15}
y \(\in\) {-17; - 7; -5; -3; -1; 1; 3; 13}
Lập bảng ta có:
| y | -17 | - 7 | -5 | - 3 | -1 | 1 | 3 | 13 |
| \(x\) = \(\dfrac{15}{y+2}\)+ 1 | 0 | - 2 | -4 | - 14 | 16 | 6 | 4 | 2 |
Theo bảng trên ta có:
các cặp số nguyên \(x;y\) thỏa mãn đề bài là:
(\(x\);y) = (0; -17); (-2; -7); (-4; -5); (-14; - 3); (16; -1); (6; 1); (4; 3); (2; 13)
Vậy: (\(x;y\)) = (0; -17); (-2; -7); (-4; -5); (-14; - 3); (16; -1); (6; 1); (4; 3); (2; 13)

Số tiền bạn Bình phải trả khi mua robot là:
\(300000\cdot\left(1-15\%\right)=255000\left(đồng\right)\)
Số tiền bạn Bình phải trả khi mua lego là:
595000-255000=340000(đồng)
Giá niêm yết của 1 con lego là:
340000:(1-15%)=400000(đồng)

a) Để xác định điểm nào nằm giữa hai điểm còn lại trong ba điểm M, N, E, chúng ta có thể sử dụng tính chất cơ bản của đoạn thẳng. Nếu E nằm giữa M và N, thì EM + EN = MN. Nếu không, thì hoặc M nằm giữa E và N hoặc N nằm giữa E và M.
Trong trường hợp này, AE = 4 cm và EM + EN = MN = 10 cm. Vì vậy, điểm E nằm giữa M và N.
b) Để tính độ dài đoạn thẳng EN, ta sử dụng công thức Euclid:
EN = MN - EM = 10 cm - 4 cm = 6 cm.
c) Giờ chúng ta cần tính độ dài ED. Vì N là điểm giữa của EM, nên EN = 6 cm.
Ta biết rằng ND = 3 cm. Do đó, ED = EN + ND = 6 cm + 3 cm = 9 cm.

đáp án: 70/100=30/X<=>(100×30)÷70=xấp xỉ 42,857
chốt lại nếu 70cm tương đương với 100% thì 30cm tương đương với xấp xỉ 42,857%
Để tính tỉ số phần trăm của 30cm so với 70cm, ta sẽ thực hiện phép tính sau:
\[
\text{Tỉ số phần trăm} = \left( \frac{30}{70} \right) \times 100
\]
\[
\text{Tỉ số phần trăm} = \left( \frac{3}{7} \right) \times 100
\]
\[
\text{Tỉ số phần trăm} = 42.857...
\]
Làm tròn đến hàng phần trăm, tức là chúng ta sẽ làm tròn 42.857... thành 43%.
Vậy nên, tỉ số phần trăm của 30cm so với 70cm là khoảng 43%.

Ta có: \(A-1=\dfrac{10^8+2}{10^8-1}-1=\dfrac{3}{10^8-1}\)
\(B-1=\dfrac{10^8}{10^8-3}-1=\dfrac{3}{10^8-3}\)
Lại có \(10^8-1>10^8-3>0\Rightarrow\dfrac{3}{10^8-3}>\dfrac{3}{10^8-1}\)
\(\Rightarrow B-1>A-1\)
\(\Rightarrow B>A\)

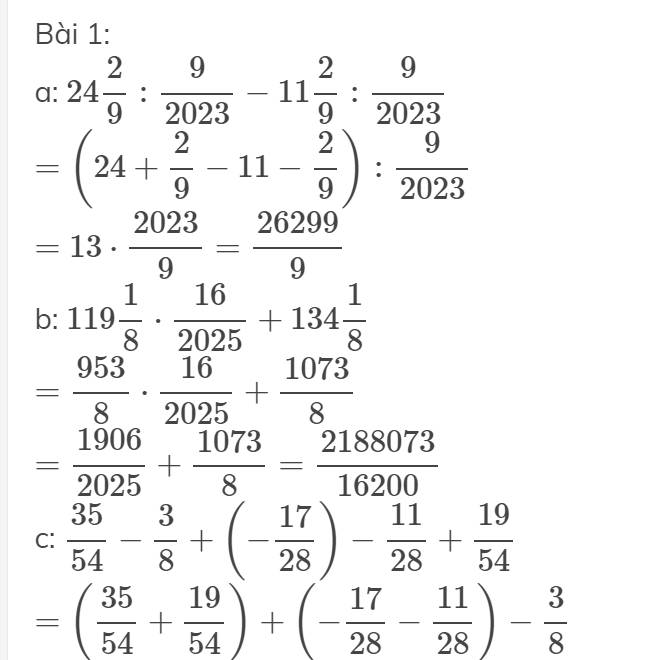
a: Sửa đề: \(24\dfrac{2}{9}:\dfrac{9}{2023}-11\dfrac{2}{9}:\dfrac{9}{2023}\)
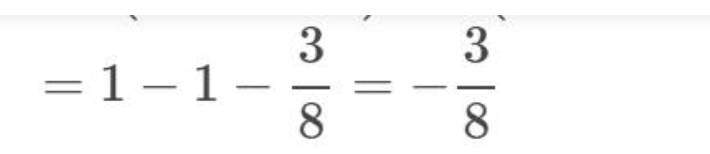

lớp 6a có số học sinh nam là:
40 : 100 x 40 = 16 ( học sinh )
lớp 6a có số học sinh nữ là:
40 - 16 = 24 ( học sinh )
hoặc
tỉ số phần trăm số học sinh nữ và số học sinh cả lớp là:
100% - 40% = 60%
lớ 6a có số học sinh là:
40 : 100 x 60 = 24 ( học sinh )

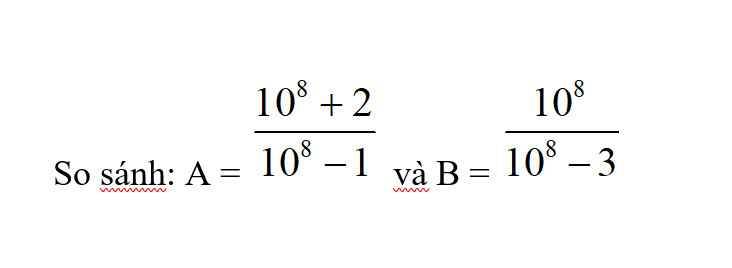
Câu 2:
a) Ta thấy: \(-0,3< 0\) mà \(\dfrac{2}{7}>0\)
\(\Rightarrow-0,3< \dfrac{2}{7}\)
b) Ta có: \(\dfrac{-3}{15}=\dfrac{-1}{5}\)
Vì \(-1>-2\Rightarrow\dfrac{-1}{5}>\dfrac{-2}{5}\)
hay \(-\dfrac{3}{15}>\dfrac{-2}{5}\)
c) Ta thấy: \(6,345>6,325\Rightarrow-6,345< -6,325\)
Câu 3:
1.
a) \(\dfrac{-5}{9}+\dfrac{4}{5}+\dfrac{-4}{9}+\dfrac{1}{5}\)
\(=\left(\dfrac{-5}{9}+\dfrac{-4}{9}\right)+\left(\dfrac{4}{5}+\dfrac{1}{5}\right)\)
\(=-1+1=0\)
b) \(-\left(7,88-2,13\right):2,3\)
\(=-5,75:2,3=-2,5\)
c) \(\left[\left(-36,56\right)+\left(-25,3\right)\right]:\left(0,25\cdot40\right)\)
\(=\left[\left(-36,56\right)+\left(-25,3\right)\right]:10\)
\(=-61,86:10=-6,186\)
Câu 3:
2. Số học sinh giỏi lớp 6B là:
\(35\cdot\dfrac{1}{5}=7\) (học sinh)
Tỉ số phần trăm của học sinh giỏi so với học sinh cả lớp là:
\(\dfrac{7}{35}\cdot100\%=20\%\)