Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tương tự như số 3 1000 số tự nhiên đầu tiên thì số 9 xuất hiện 300 lần

Vì số 1000 không có chữ số 3 nên ta xét các số tự nhiên từ 0 đến 999. Nếu ta viết thêm 2 chữ số 0 vào trước các số có 1 chữ số, và 1 chữ số 0 vào trước các số có 2 chữ số thì từ 0 đến 999 trở thành các số có 3 chữ số. Từ 000 đến 999 có số số hạng là:
(999 - 000) : 1 + 1 = 1000 (số)
Số chữ số từ 000 đến 999 là: 3 \(\times\) 1000 = 3 000 (chữ số)
Vậy từ 0 đến 999 Chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; ;9 xuất hiện số lần như nhau và xuất hiện số lần là:
3 000 : 10 = 300 (lần)
Đáp số: 300 lần
Xét từ 1-100
Số chữ số 3 ở hàng đơn vị: \(\left(3,13,23,43,53,63,73,83,93\right)\)10 chữ số
Số chữ số 3 ở hàng chục: \(\left(30,31,32,33,34,35,36,37,38,39\right)\) 10 chữ số
Như vậy cứ 100 số thì chữ số 3 sẽ xuất hiện 20 lần (chỉ tính ở hàng chục và hàng đơn vị)
Xét từ 1-1000
Sồ chữ số 3 ở hàng chục và hàng đơn vị: \(20.10=200 \)(chữ số)
Số chữ số 3 ở hàng trằm \(\left(300,301,302,303,...,399\right)=100\) chữ số
Vậy số lần chữ số 3 xuất hiện: \(100+200=300\) (lần)

Kiến thức cần nhớ:
Tùy theo yêu cầu của dề bài, em sẽ vẽ các tập hợp trong vòng kín giao nhau cho phù hợp em nhé.
Phần giao nhau của hai tập hợp hoặc nhiều tập hợp thì đó sẽ gồm các phần tử chung của hai tập hợp

\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.

`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)

Ta có: \(C=\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}\)
\(C=\dfrac{abc}{a^3}+\dfrac{abc}{b^3}+\dfrac{abc}{c^3}\)
\(C=abc\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)\)
Vì: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{c}\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^3=\left(-\dfrac{1}{c}\right)^3\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{3}{ab}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=-\dfrac{1}{c^3}\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+\dfrac{3}{ab}\left(-\dfrac{1}{c}\right)=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+-\dfrac{3}{abc}=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\left(1\right)\)
Thay (1) vào C ta được:
\(C=abc\left(\dfrac{3}{abc}\right)\)
\(\Rightarrow C=3\)

Giả sử \(ab< ba\), theo đề bài \(ab=a+b+27\rightarrow10a+b=a+b+27\)
\(\Rightarrow9a=27\)
\(\Rightarrow a=3\)
Số sẽ có dạng \(3b\)
- Theo bài \(3b\cdot b3=3154\Rightarrow\left(30+b\right)\left(10b+3\right)=3154\)
\(\Rightarrow300b+90+10b^2+3b=3154\)
\(\Rightarrow10b^2+303b-3064=0\)
\(\Rightarrow\Delta=b^2-4ac=303^2-4\cdot10\cdot\left(-3064\right)=\text{214369 }\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-303+\sqrt{214369}}{2\cdot10}=8\left(tm\right)\\x_2=\dfrac{-303-\sqrt{214369}}{2\cdot10}=-\dfrac{383}{10}\left(ktm\right)\end{matrix}\right.\)
Vậy số cần tìm là 38 hoặc 83

a) \(\left(-x-4\right)^2\)
\(=\left(-x\right)^2-2\cdot\left(-x\right)\cdot4+4^2\)
\(=x^2+8x+16\)
b) \(\left(-5+3x\right)^2\)
\(=\left(-5\right)^2+2\cdot\left(-5\right)\cdot3x+\left(3x\right)^2\)
\(=25-30x+9x^2\)
c) \(\left(-x-3\right)\left(x-3\right)\)
\(=-\left(x+3\right)\left(x-3\right)\)
\(=-\left(x^2-9\right)\)

Hiệu số phần bằng nhau là :
`9-4=5` ( phần )`
Chiều dài hình chữ nhật là :
`11,5 : 5 xx 9=20,7(m)`
Chiều rộng hình chữ nhật là :
`20,7 - 11,5=9,2(m)`
Chu vi hình chữ nhật là :
`(20,7 + 9,2 ) xx 2=59,8(m)`
Diện tích hình chữ nhật là :
`20,7 xx 9,2=190,44(m^2)`
Hiệu số phần bằng nhau là :
9-4=5 ( phần )
Chiều dài hình chữ nhật là :
11,5 : 5 xx 9=20,7(m)
Chiều rộng hình chữ nhật là :
20,7 - 11,5=9,2(m)
Chu vi hình chữ nhật là :
(20,7 + 9,2 ) x 2=59,8(m)
Diện tích hình chữ nhật là :20,7 xx 9,2=190,44(m^2
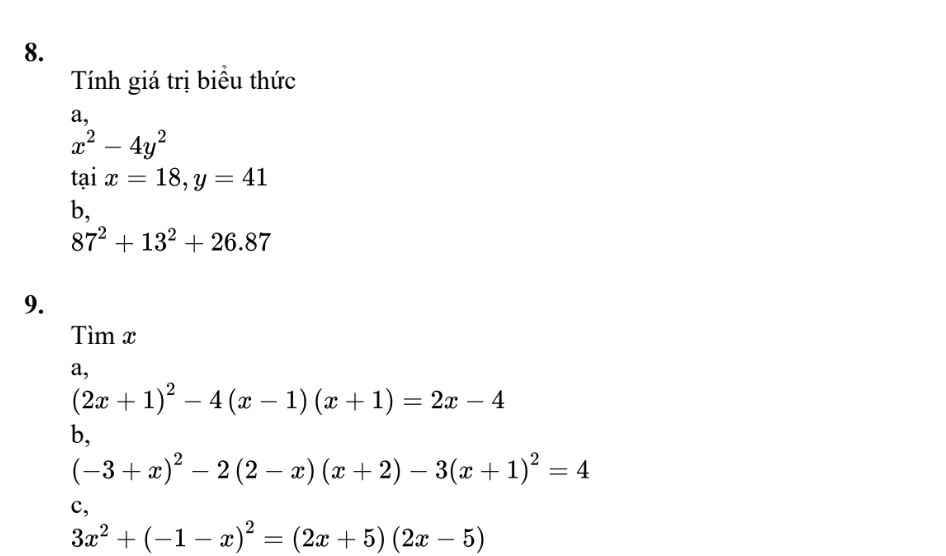
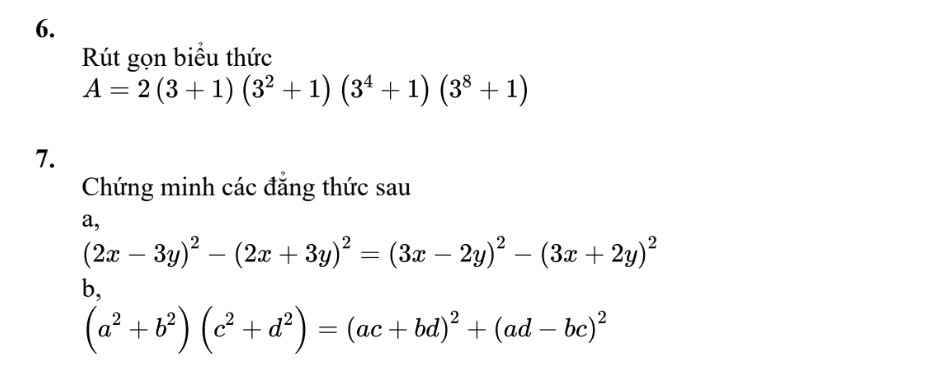
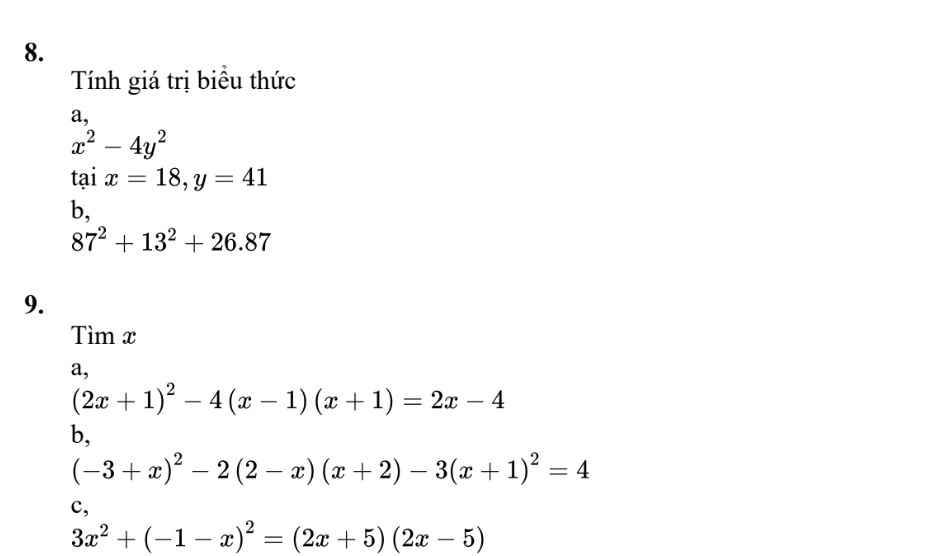

Ta có
100 x a + 10 x b + c + 10 x a + b + a = 732
111 x a + 11 x b + c = 732
=> a = 6
11 x b + c = 732 - 666
11 x b + c = 66 = 11 x 6 + 0
Vậy b = 6, c = 0
Vậy số cần tìm là 660
Ta có : abc + ab+a =732
=> 100a + 10b +c +10a + b+a=732
=> 111a + 11b + c = 732
Khi đó ta thấy :
<=> 111a < 732 => a < 7
Lại có : 11b + c < 11.10 + 10
=> 11b + c < 120 nên 111a > 732 - 120
=> 111a > 612 => a > 5
<=> a = 6
Vì a = 6 => 666 + 11b + c = 732
=> 11b + c = 732 - 666
=> 11b + c = 66 => 11b < 66 => b < 6 mà c < 10 nên 11b > 56 => b > 4
<=> b = 5 và c = 9
⇒⇒abc = 659