
 Giúp mik !❤
Giúp mik !❤
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{mOn};\widehat{mOt}\) là hai góc kề bù
=> \(\widehat{mOn}+\widehat{mOt}=180^o\)
Mà: \(\widehat{mOn}=50^o\)
\(=>50^o+\widehat{mOt}=180^o\\ =>\widehat{mOt}=180^o-50^o\\ =>\widehat{mOt}=130^o\)

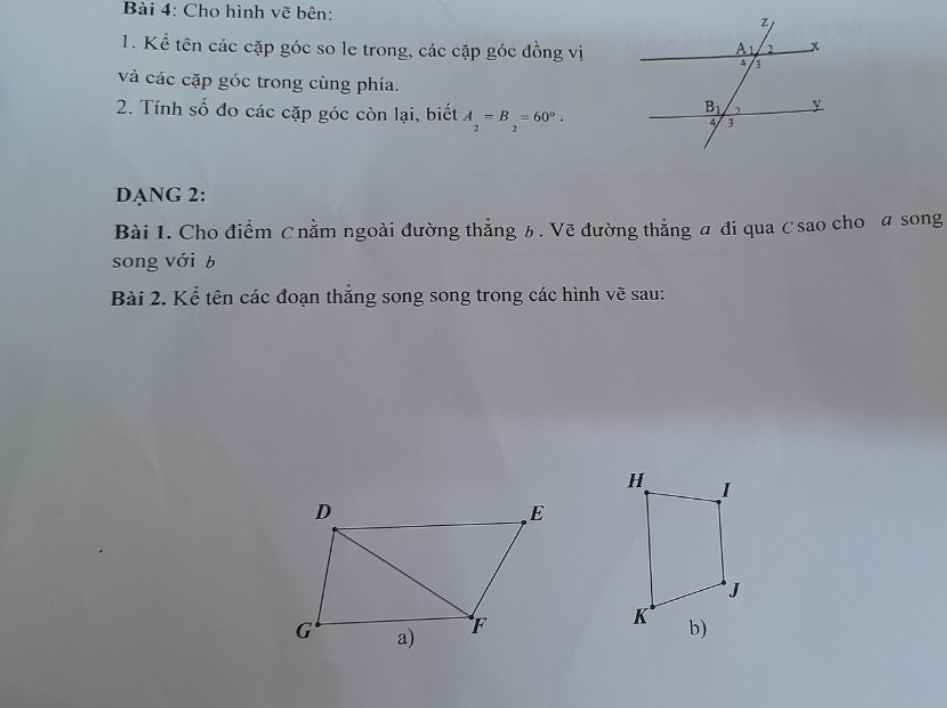
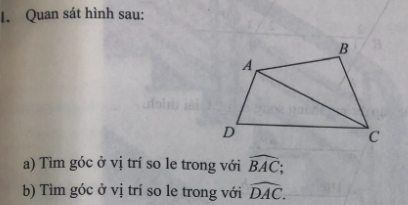
a: Góc so le trong với \(\widehat{BAC}\) là góc ACD
b: Góc so le trong với \(\widehat{DAC}\) là góc BCA

Bài 5:
a) Oc nằm giữa Oa và Ob
=> \(\widehat{aOb}=\widehat{aOc}+\widehat{cOb}\)
\(=>\widehat{cOb}=\widehat{aOb}-\widehat{aOc}=100^o-40^o=60^o\)
b) Od là phân giác của \(\widehat{cOb}\)
=> \(\widehat{cOd}=\widehat{dOb}\)
Mà: \(\widehat{cOd}+\widehat{dOb}=\widehat{cOb}=>2\widehat{cOd}=60^o\)
\(=>\widehat{cOd}=\dfrac{60^o}{2}=30^o\)
6:
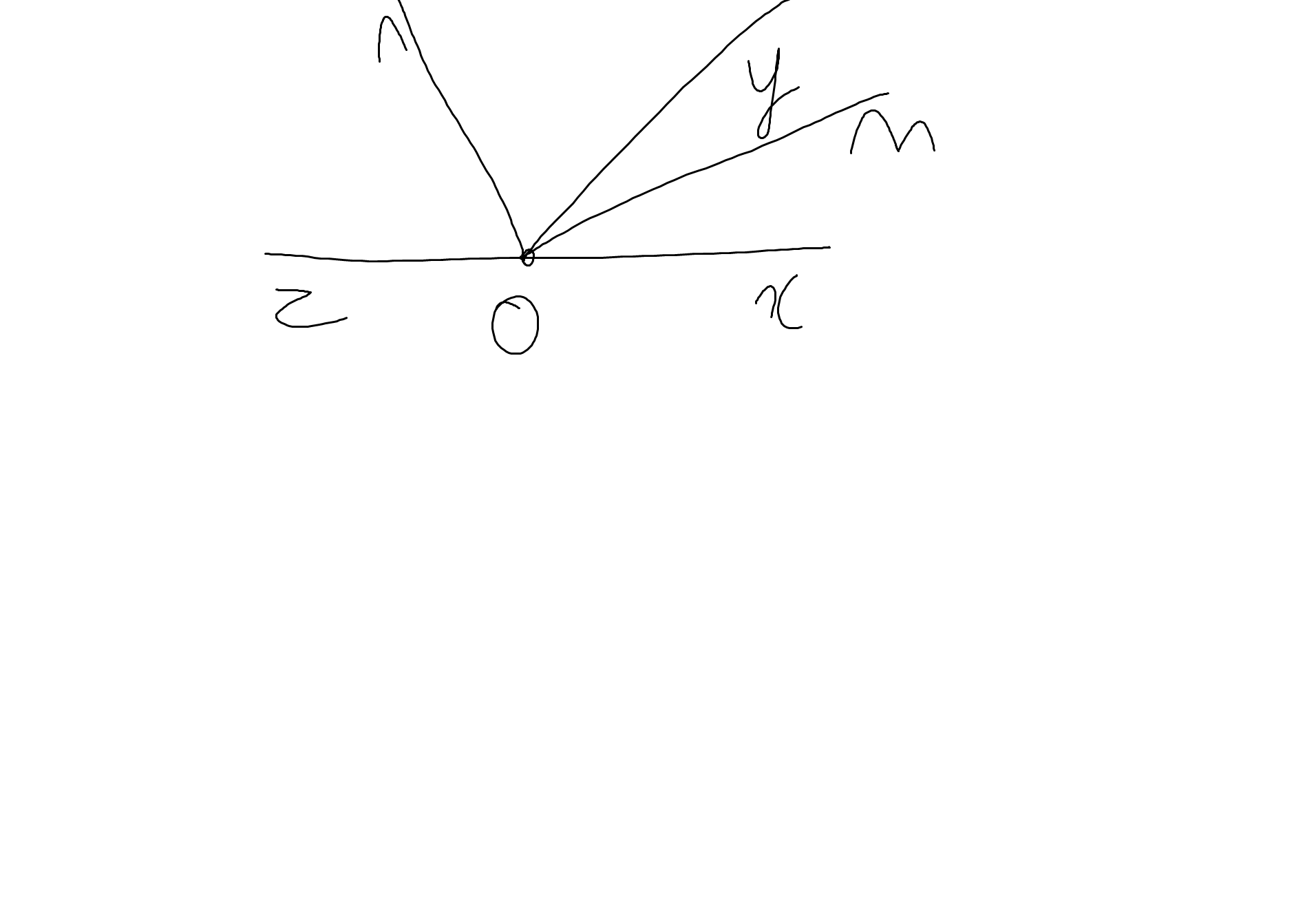
Ta có: \(\widehat{xOy}+\widehat{zOy}=180^0\)
=>\(\widehat{zOy}=180^0-60^0=120^0\)
Om là phân giác của góc xOy
=>\(\widehat{yOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: On là phân giác của góc yOz
=>\(\widehat{yOn}=\dfrac{\widehat{yOz}}{2}=\dfrac{120^0}{2}=60^0\)
\(\widehat{mOn}=\widehat{yOm}+\widehat{yOn}=30^0+60^0=90^0\)

\(\widehat{A}=180^o-\widehat{B}-\widehat{C}=180^o-40^o-40^o=100^o\)
=> \(\widehat{A_{ngoai}}=180^o-100^o=80^o\)
=> \(\widehat{DAB}=\dfrac{1}{2}\widehat{A_{ngoai}}=\dfrac{1}{2}\cdot80^o=40^o\)
Ta có: \(\widehat{DAB}=\widehat{ABC}\left(=40^o\right)\)
Mà 2 góc này ở vị trí so le trong
=> AD//BC

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(2\cdot\left(\widehat{OBC}+\widehat{OCB}\right)=90^0\)
=>\(\widehat{OBC}+\widehat{OCB}=45^0\)
Xét ΔOBC có \(\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180^0\)
=>\(\widehat{BOC}+45^0=180^0\)
=>\(\widehat{BOC}=135^0\)

ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=100^0\)
AD là phân giác góc ngoài tại đỉnh A
=>\(\widehat{CAD}=\dfrac{180^0-\widehat{BAC}}{2}=40^0\)
=>\(\widehat{CAD}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC

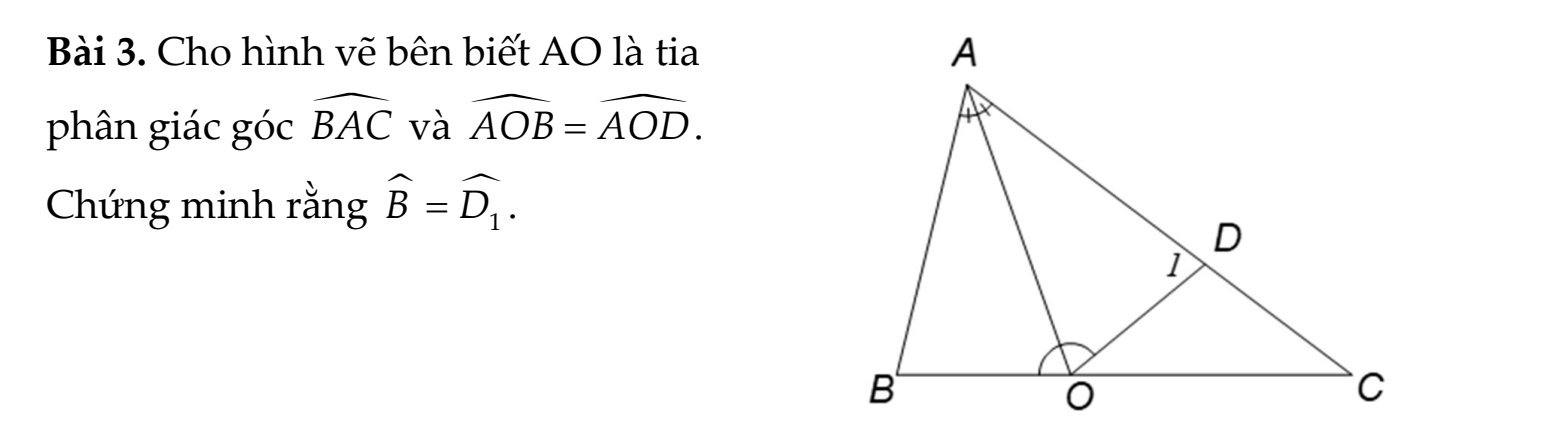
Xét 2 ΔABO và ΔADO ta có:
\(\widehat{BAO}=\widehat{DAO}\) (AD là phân giác của góc BAC)
\(OA\) chung
\(\widehat{AOB}=\widehat{AOD}\left(gt\right)\)
\(=>\Delta ABO=\Delta ADO\left(g.c.g\right)\)
\(=>\widehat{B}=\widehat{D_1}\) (hai góc tương ứng)

\(2^2+3^2+...+2021^2\)
\(=\left(1^2+2^2+...+2021^2\right)-1\)
\(=\dfrac{2021\cdot\left(2021+1\right)\left(2\cdot2021+1\right)}{6}=1\)
\(=2753594310\)
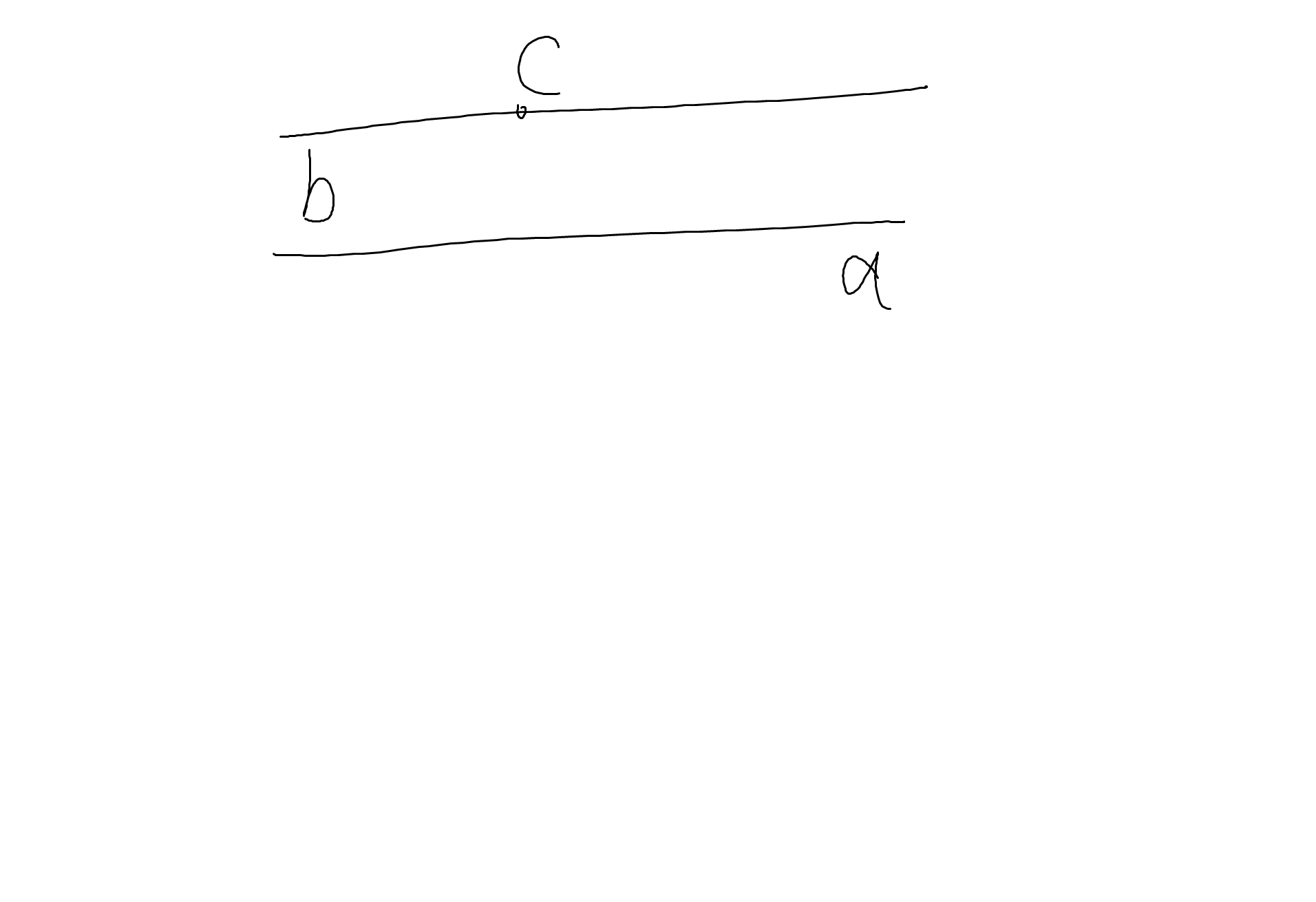
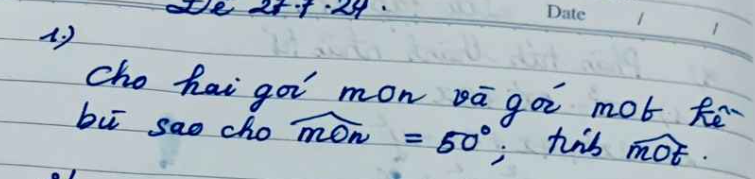




Bài 6: Kẻ Dm//Ax
Vì Dm//Ax
nên \(\widehat{mDA}+\widehat{xAD}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{mDA}=180^0-150^0=30^0\)
Ta có: \(\widehat{mDA}+\widehat{mDE}=\widehat{ADE}\)
=>\(\widehat{mDE}=80^0-30^0=50^0\)
Vì \(\widehat{mDE}+\widehat{yED}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên Dm//Ey
=>Ax//Ey
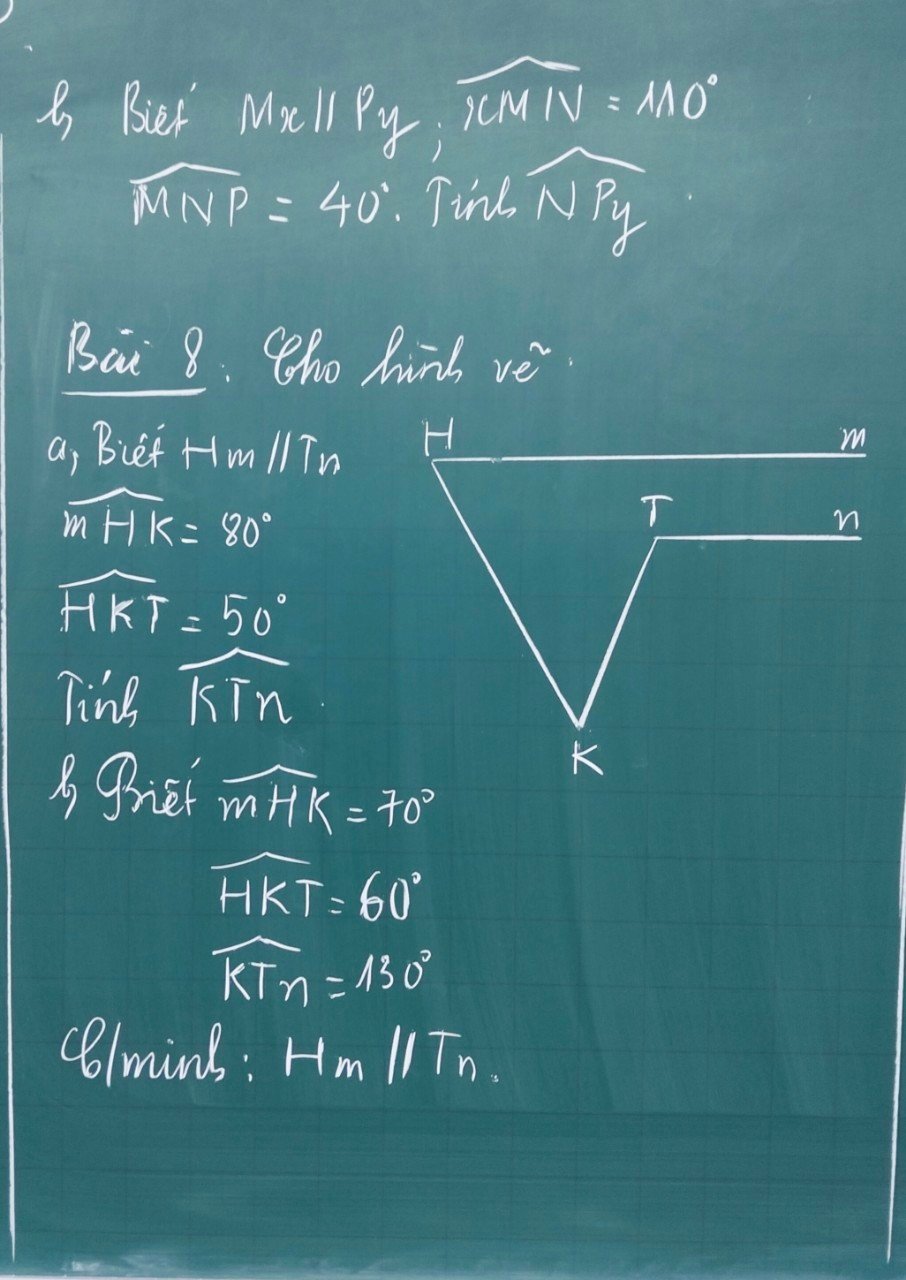
Bài 8:
a: Gọi A là giao điểm của KT với Hm
Xét ΔKAH có \(\widehat{KAH}+\widehat{KHA}+\widehat{AKH}=180^0\)
=>\(\widehat{KAH}=180^0-80^0-50^0=50^0\)
Vì Hm//Tn nên \(\widehat{nTA}=\widehat{TAH}=50^0\)
\(\widehat{nTA}+\widehat{nTK}=180^0\)(hai góc kề bù)
=>\(\widehat{nTK}=180^0-50^0=130^0\)
b: Gọi A là giao điểm của KT với Hm
Xét ΔKAH có \(\widehat{KAH}+\widehat{KHA}+\widehat{HKA}=180^0\)
=>\(\widehat{KAH}+70^0+60^0=180^0\)
=>\(\widehat{KAH}=50^0\)
Ta có: \(\widehat{nTK}+\widehat{nTA}=180^0\)(hai góc kề bù)
=>\(\widehat{nTA}=180^0-130^0=50^0\)
Ta có: \(\widehat{nTA}=\widehat{HAK}\left(=50^0\right)\)
mà hai góc này là hai góc so le trong
nên Hm//Tn
Giúp mik giải bài 7 với ạ ! ❤