Các số tự nhiên nhỏ hơn `100` là : 

`1;2;3;4;...;99`

Khoảng cách : `1`

Số số hạng là :\(\dfrac{99-1}{1}+1=99\)

Tổng là : \(\dfrac{99+1\times99}{2}=4950\)

Ta có dãy các số tự nhiên nhỏ hơn 100: 0;1;2;3;...;99

Dãy có số số hạng là: (99-0):1+1=100 (số hạng)

Tổng của dãy là: (99+0)x100:2= 4950

Góc nhọn: \(\widehat{ABD};\widehat{ADB};\widehat{BEC};\widehat{EDC};\widehat{BDC};\widehat{ECD};\widehat{BCE};\widehat{BCD}\)

Góc vuông: \(\widehat{BAD}\)

Góc tù: \(\widehat{DBC};\widehat{EBC};\widehat{DEC}\)

a, Góc nhọn: \(\widehat{ABD}\);  \(\widehat{BCE}\); \(\widehat{BCD}\); \(\widehat{DCE}\); \(\widehat{BDC}\); \(\widehat{ADB}\); \(\widehat{BEC}\)

b, Góc vuông: \(\widehat{BAD}\); \(\widehat{ADC}\)

c, Góc tù: \(\widehat{ABC}\);  \(\widehat{CBD}\); \(\widehat{CED}\)

\(x\) \(\times\) \(\dfrac{14}{3}\) = 2,5

\(x\)           = 2,5 : \(\dfrac{14}{3}\) 

\(x\)           = \(\dfrac{15}{28}\)

x.14/3=2,5

x        =2,5:14/3

x        =15/28

Chúc bn hok tốt!!!

Trước hết ta phải chứng minh \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).

Thật vậy, \(\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{a+ab}{b^2+b}\) và \(\dfrac{a+1}{b+1}=\dfrac{\left(a+1\right)b}{\left(b+1\right)b}=\dfrac{ab+b}{b^2+b}\).

Mà theo giả thuyết là a < b nên \(\dfrac{a+ab}{b^2+b}< \dfrac{ab+b}{b^2+b}\), suy ra \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).

Từ đây ta có:

\(B=\dfrac{2022^{2022}+1}{2022^{2023}+1}=\dfrac{2022^{2023}+2022}{2022^{2024}+2022}=\dfrac{2022^{2023}+2021+1}{2022^{2024}+2021+1}\)

Đặt \(A_1=\dfrac{2022^{2023}+2}{2022^{2024}+2}=\dfrac{2022^{2023}+1+1}{2022^{2024}+1+1}\), rõ ràng \(A_1>A\).

Đặt \(A_2=\dfrac{2022^{2023}+3}{2022^{2024}+3}=\dfrac{2022^{2023}+2+1}{2022^{2024}+2+1}\), rõ ràng \(A_2>A_1\).

...

Đặt \(A_{2020}=\dfrac{2022^{2023}+2021}{2022^{2024}+2021}=\dfrac{2022^{2023}+2020+1}{2022^{2024}+2020+1}\), rõ ràng \(A_{2020}>A_{2019}\) và \(B>A_{2020}\).

Suy ra \(B>A_{2020}>A_{2019}>...>A_2>A_1>A\). Vậy A < B.

Ta có A = \(\dfrac{2022^{2023}}{2022^{2024}}=\dfrac{1}{2022}\) ; B = \(\dfrac{2022^{2022}}{2022^{2023}}=\dfrac{1}{2022}\)

Mà \(\dfrac{1}{2022}=\dfrac{1}{2022}\)

Vậy A = B

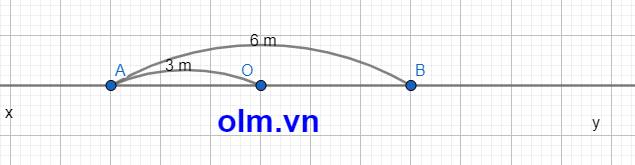
a, Các cặp tia đối nhau chung gốc A lần lượt là:

Ax và AO;  Ax và AB;  Ax và AY 

b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B

      ⇒ OA + OB = AB 

      ⇒ OB = AB - OA

         Độ dài đoạn OB là: 6 - 3 = 3 (cm)

  c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB 

`@` `\text {Ans}`

`\downarrow`

`xy100(z+1)`

`= (xy100)*z + xy100`

`= xyz100 + xy100`

Vì đa thức là tổng của những đơn thức bao gồm biến và hệ số

Vậy, biểu thức trên là đa thức.

không

a: Trên tia Ox, ta có: OM<ON

nên M nằm giữa O và N

=>OM+MN=ON

=>MN+4=8

=>MN=4(cm)

b: Ta có: M nằm giữa O và N

MN=MO(=4cm)

Do đó: M là trung điểm của ON

c: Trên tia Ox, ta có: OP<OM

nên P nằm giữa O và M

=>OP+PM=OM

=>PM+2=4

=>PM=2(cm)

Ta có: P nằm giữa O và M

mà OP=PM(=2cm)

nên P là trung điểm của OM

Trên tia Ox, ta có: OM<OQ

nên M nằm giữa O và Q

=>OM+MQ=OQ

=>MQ+4=6

=>MQ=2(cm)

Vì MP=MQ(=2cm)

nên M là trung điểm của PQ

Trên tia Ox, ta có: OQ<ON

nên Q nằm giữa O và N

=>OQ+QN=ON

=>QN+6=8

=>QN=2(cm)

Vì MQ=QN(=2cm)

nên Q là trung điểm của MN

`@` `\text {Ans}`

`\downarrow`

`0,3x+1,2=2/3x+9/10`

`=> 0,3x + 1,2 - 2/3x - 9/10 = 0`

`=> (0,3-2/3)x + (1,2-9/10) = 0`

`=> (-11/30x) + 3/10 = 0`

`=> -11/30x = -3/10`

`=> x = -3/10 \div (-11/30)`

`=> x = 9/11`

Vậy, `x=9/11`

`@` `\text {Kaizuu lv uuu}`

Áp dụng phương pháp chuyển vế đổi dấu, em chuyển tất cả các hạng tử chứa ẩn \(x\) sang một bên, các hạng tử không chứa \(x\) sang một bên, đồng thời đổi dấu các hạng tử vừa chuyển.

            0,3\(x+1,2=\dfrac{2}{3}x+\dfrac{9}{10}\)

            \(\dfrac{2}{3}x-0,3x=1,2-\dfrac{9}{10}\)

            \(\left(\dfrac{2}{3}-0,3\right)x\) = 0,3

                 \(\dfrac{11}{30}x\) = 0,3

                      \(x\) = 0,3 : \(\dfrac{11}{30}\)

                       \(x\) = \(\dfrac{9}{11}\)

mình biết làm rồi. xin lỗi đã làm phiền mọi người