a; độ dài đoạn thẳng AB là:

AB = AC - BC = 10 - 6 = 4 (cm)

b; độ dài đoạn thẳng CD là:

CD = BD - BC = 12 - 6 = 6 (cm)

=> CD = BC

=> C là trung điểm đoạn thẳng BD

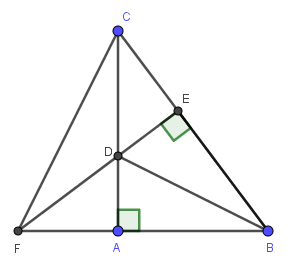
a) Do \(BD\) là tia phân giác của \(\widehat{ABC}\left(gt\right)\)

\(\Rightarrow\widehat{ABD}=\widehat{CBD}\)

\(\Rightarrow\widehat{ABD}=\widehat{EBD}\)

Xét hai tam giác vuông: \(\Delta BAD\) và \(\Delta BED\) có:

\(BD\) là cạnh chung

\(\widehat{ABD}=\widehat{EBD}\left(cmt\right)\)

\(\Rightarrow\Delta BAD=\Delta BED\) (cạnh huyền - góc nhọn)

b) Do \(\Delta BAD=\Delta BED\left(cmt\right)\)

\(\Rightarrow AD=ED\) (hai cạnh tương ứng)

Xét hai tam giác vuông: \(\Delta ADF\) và \(\Delta EDC\) có:

\(AD=ED\left(cmt\right)\)

\(\widehat{ADF}=\widehat{EDC}\) (đối đỉnh)

\(\Rightarrow\Delta ADF=\Delta EDC\) (cạnh góc vuông - góc nhọn kề)

\(AF=EC\) (hai cạnh tương ứng)

c) Do \(\Delta BAD=\Delta BED\left(cmt\right)\)

\(\Rightarrow BA=BD\) (hai cạnh tương ứng)

Lại có:

\(AF=CE\left(cmt\right)\)

\(\Rightarrow BA+AF=BE+EC\)

\(\Rightarrow BF=BC\)

\(\Rightarrow\Delta BCF\) cân tại B

a)

Xét △BAD và △BED , ta có :

góc BAD = góc BED ( cùng bằng 90°)

BD là cạnh chung

∠ABD = ∠EBD (BD là tia phân giác)

⇒ △BAD = △BED (cạnh huyền - góc nhọn)

b)

Từ △BAD = △BED ⇒ BA = BE và DA = DE

Xét △ADF và △EDC:

DA = DE

gócADF = góc EDC (đối đỉnh)

∠FAD = ∠CED = 90°

⇒ △ADF = △EDC (g. c .g)

⇒ AF = EC

c) Từ BA = BE ⇒ △BAE cân tại B

⇒ gócBAE = gócBEA

Từ △ADF = △EDC ⇒ góc AFD = góc ECD

Mà gócAFD = ∠BFC (đối đỉnh) ⇒ góc BFC = gócECD

Ta có:

gócBCF = góc BCE + gócECF

gócBFC = gócECD

Suy ra: gócBCF = gócBFC

⇒ △BCF cân tại B

\(1,4x-x=-8,844\\ 0,4x=-8,844\\ x=\dfrac{-8,844}{0,4}=-22,11\)

a. xét ΔABH và ΔACH, có:

AB = AC (ΔABC cân tại A)

\(\widehat{ABC}=\widehat{ACB}\left(\text{Δ}ABC\text{ cân tại A}\right)\)

HB = HC (H là trung điểm BC)

=> ΔABH = ΔACH (c-g-c)

b. trong ΔABC cân tại A có AH là đường trung tuyến

=> AH cũng là đường phân giác

\(=>\widehat{DAH}=\widehat{EAH}\) (1)

xét Δ vuông DAH và Δ vuông EAH có:

AH là cạnh chung; \(\widehat{DAH}=\widehat{EAH}\) (từ (1))

=> Δ DAH = Δ EAH (ch-gn)

=> HD = HE (2 cạnh tương ứng)

=> ΔHDE là Δ cân (tại H)

c. ta có Δ DAH = Δ EAH (câu b)

=>  AD = AE (2 cạnh tương ứng)

=> ΔDEA là Δ cân tại A

xét ΔDEA cân tại A có: \(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\left(2\right)\)

xét ΔABC cân tại A có: \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\left(3\right)\)

từ (2) và (3) => \(\widehat{ADE}=\widehat{ABC}\)

mà 2 góc này ở vị trí đồng vị

=> DE // BC

Đây là toán nâng cao chuyên đề phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng tư duy logic như sau:

Giải:

Vì số đó chia cho 8 dư 3 nên số đó sẽ chia hết cho 8 khi thêm vào số đó là:

8 - 3 = 5(đơn vị)

Vì 8 chia hết cho 4 nên số đó khi thêm vào 5 đơn vị thì chia hết cho 8 cũng chia hết cho 4.

mà 5 chia 4 dư 1, vậy số đó ban đầu chia 4 có số dư là:

4 - 1 = 3 (đơn vị)

Số cần tìm là:

77848 x 4 + 3 = 311395

Đáp số: 311395

4,9% x 3,3 - 4,8 x 3,3 - 0,33%

= (4,9 x 0,33% - 0,33%) - 4,8 x 3,3

= 0,33%(49 - 1) - 4,8 x 3,3

= 0,33%.48 - 48 x 0,33

= 48 x (0,0033 - 0,33)

= 48 x (-0,3267)

= - 15,6816

gọi biểu thức đó là c ta có

c= 1×99 + 2×98 + 3×97 + ... + 98×2 + 99×1

C = 1×(100 - 1) + 2×(100 - 2) + 3×(100 - 3) + ... + 98×(100 - 98) + 99×(100 - 99)

C = 1×100 - 1² + 2×100 - 2² + 3×100 - 3² + ... + 98×100 - 98² + 99×100 - 99²

C = (1×100 + 2×100 + 3×100 + ... + 98×100 + 99×100) - (1² + 2² + 3² + ... + 99²)

C = 100×(1 + 2 + 3 + ... + 98 + 99) - [(1 + 0)×1 + (1 + 1)×2 + (1 + 2)×3 + ... + (1 + 98)×99]

C = 100×(1 + 99)×99:2 + (1 + 0×1 + 2 + 1×2 + 3 + 2×3 + ... + 99 + 98×99)

C = 50×100×99 + [(1 + 2 + 3 + ... + 99) + (0×1 + 1×2 + 2×3 + ... + 98×99)]

C = 495000 + [(1+99)×99:2 + (0×1 + 1×2 + 2×3 + ... + 98×99)]

C = 495000 + 50 × 99 + (0×1 + 1×2 + 2×3 + ... + 98×99)

C = 495000 + 4950 + (0×1 + 1×2 + 2×3 + ... + 98×99)

Đặt A = 0×1 + 1×2 + 2×3 + ... + 98×99

3A = 1×2×(3-0) + 2×3×(4-1) + ... + 98×99×(100-97)

3A = 1×2×3 - 0×1×2 + 2×3×4 - 1×2×3 + ... + 98×99×100 - 97×98×99

3A = (1×2×3 + 2×3×4 + ... + 98×99×100) - (0×1×2 + 1×2×3 + ... + 97×98×99)

3A = 98×99×100

A = 98×33×100

A = 323400

C = 495000 + 4950 + 323400

C = 823350

 1×99 + 2×98 + 3×97 + ... + 98×2 + 99×1

C = 1×(100 - 1) + 2×(100 - 2) + 3×(100 - 3) + ... + 98×(100 - 98) + 99×(100 - 99)

C = 1×100 - 1² + 2×100 - 2² + 3×100 - 3² + ... + 98×100 - 98² + 99×100 - 99²

C = (1×100 + 2×100 + 3×100 + ... + 98×100 + 99×100) - (1² + 2² + 3² + ... + 99²)

C = 100×(1 + 2 + 3 + ... + 98 + 99) - [(1 + 0)×1 + (1 + 1)×2 + (1 + 2)×3 + ... + (1 + 98)×99]

C = 100×(1 + 99)×99:2 + (1 + 0×1 + 2 + 1×2 + 3 + 2×3 + ... + 99 + 98×99)

C = 50×100×99 + [(1 + 2 + 3 + ... + 99) + (0×1 + 1×2 + 2×3 + ... + 98×99)]

C = 495000 + [(1+99)×99:2 + (0×1 + 1×2 + 2×3 + ... + 98×99)]

C = 495000 + 50 × 99 + (0×1 + 1×2 + 2×3 + ... + 98×99)

C = 495000 + 4950 + (0×1 + 1×2 + 2×3 + ... + 98×99)

Đặt A = 0×1 + 1×2 + 2×3 + ... + 98×99

3A = 1×2×(3-0) + 2×3×(4-1) + ... + 98×99×(100-97)

3A = 1×2×3 - 0×1×2 + 2×3×4 - 1×2×3 + ... + 98×99×100 - 97×98×99

3A = (1×2×3 + 2×3×4 + ... + 98×99×100) - (0×1×2 + 1×2×3 + ... + 97×98×99)

3A = 98×99×100

A = 98×33×100

A = 323400

C = 495000 + 4950 + 323400

C = 823350