Đây là toán nâng cao chuyên đề toán ba tỉ số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                  Giải:

Số bóng lấy ra ở hộp a là: 1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (số bóng hộp a lúc đầu)

Số bóng lấy ra ở hộp b là: 1 - \(\dfrac{2}{11}\) = \(\dfrac{9}{11}\) (số bóng hộp b lúc đầu)

Số bóng lấy ra ở hộp c là: 1 - \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) (số bóng hộp c lúc đầu)

Số bóng hộp b lúc đầu bằng: 

    \(\dfrac{1}{2}\): \(\dfrac{9}{11}\) = \(\dfrac{11}{18}\)(số bóng hộp a lúc đầu)

 Số bóng hộp c lúc đầu bằng:

     \(\dfrac{1}{2}\) : \(\dfrac{2}{3}\) = \(\dfrac{3}{4}\) (số bóng hộp a lúc đầu)

210 quả bóng ứng với:

     1 + \(\dfrac{11}{18}\) + \(\dfrac{3}{4}\) = \(\dfrac{85}{36}\)(số bóng hộp a lúc đầu)

Số bóng hộp a lúc đầu là:

      210 : \(\dfrac{85}{36}\)= \(\dfrac{1512}{17}\) (quả)

Đây không phải là số tự nhiên nên không có số bóng nào thỏa mãn đề bài. 

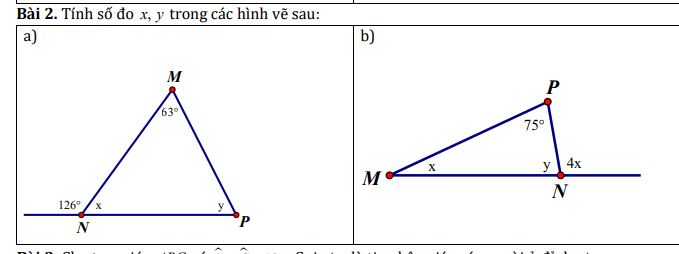
`a)`có : 

\(126^0+x=180^0\)(kề bù)

`=>`\(x=180^0-126^0=54^0\)

xét `ΔMNP` có :

\(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)

`=>`\(\widehat{P}=x=180^0-63^0-54^0=63^0\)

`b)` gọi `Nz` là tia đối của `NM`

có : \(\widehat{PMz}\) là góc ngoài `ΔPNM`

`=>`\(4x=75^0+x\)

`=>`\(4x-x=75^0\)

`=>`\(3x=75^0\)

`=>x = 25^0`

Lại có : \(\widehat{PNM}+\widehat{PNz}=180^0\)(kề bù)

`=>`\(y+4\cdot25^0=180^0\)

`=> y+ 100^0 = 180^0`

`=> y = 180^0 - 100^0`

`=> y = 80^0`

a: \(\left\{{}\begin{matrix}11\cdot4^{14}⋮4\\16^{15}=4^{30}⋮4\end{matrix}\right.\)

Do đó: \(11\cdot4^{14}+16^{15}⋮4\)

b: \(\left\{{}\begin{matrix}24\cdot8^{23}=8^{23}\cdot8\cdot3⋮3\\171=3\cdot57⋮3\end{matrix}\right.\)

Do đó: \(24\cdot8^{23}-171⋮3\)

c: \(126⋮9\)

=>\(126^3⋮9\)

=>\(126^3\cdot13^2⋮9\)(2)

\(3^{24}=3^2\cdot3^{22}=9\cdot3^{22}⋮9\)

=>\(2\cdot3^{24}⋮9\)(1)

Từ (1),(2) suy ra \(126^3\cdot13^2+2\cdot3^{24}⋮9\)

Nếu có chỗ nào chưa hiểu em có thể liên hệ

zalo: 0385 168 017 để được giảng miễn phí.

a; 11.4¹⁴ + 16¹⁵

= 11.4¹⁴ + (4²)¹⁵

= 4.(11.4¹³ + 4²⁹) ⋮ 4 (đpcm)

b; 24.8²³ - 171 

=  3.(8.8²³ - 57) ⋮ 3 (đpcm)

c;  126³.13² + 2.3²⁴

  = (9.14)³.13² + 2.(3²)¹²

  =  9³.14³.13² + 2.9¹² 

= 9³.(14³.13² + 2.9⁹) ⋮ 9 (đpcm)

   \(\dfrac{3}{7}\) + \(\dfrac{30}{18}\) + \(\dfrac{33}{21}\) - \(\dfrac{6}{9}\)

=  \(\dfrac{3}{7}\) + \(\dfrac{15}{9}\) + \(\dfrac{11}{7}\) - \(\dfrac{6}{9}\)

= (\(\dfrac{3}{7}\) + \(\dfrac{11}{7}\)) + (\(\dfrac{15}{9}\) - \(\dfrac{6}{9}\))

= 2 + 1

= 3

  \(x^2\)(\(x\) - 3) - \(x\)( 3 - \(x\))²

= \(x^3\) - 3\(x^2\) - \(x\)(9 - 6\(x\) + \(x\)²)

= \(x^3\) - 3\(x^2\) - 9\(x\) + 6\(x^2\) - \(x^3\)

= (\(x^3\) - \(x^3\)) + (6\(x^2\) - 3\(x^2\)) - 9\(x\)

= 0 + 3\(x^2\) - 9\(x\)

= 3\(x^2\) - 9\(x\) 

Số nghịch đảo của `8/15` là `15/8`

Số nghịch đảo của `1/4` là `4`

         Kiến thức cần nhớ:

Chỉ có những phân số có tử, mẫu khác không mới có phân số nghịch đảo.

Muốn tìm phân số nghịch đảo ta chỉ cần đảo ngược tử số và phân số ban đầu. 

`10+5.(x-13)=35`

`5.(x-13)=35-10`

`5.(x-13)=25`

`x-13=25:5`

`x-13=5`

`x=5+13`

`x=18`

\(\left(n+8\right)\) chia hết `(n+3)`

`(n+3)+5` chia hết `(n+3)`

`5` chia hết cho `(n+3)`

Nên `(n+3)` là ước của 5

Mà n là số tự nhiên nên \(n+3\ge3\)

Suy ra `n+3=5`

Suy ra `n=2`

  Đây là toán nâng cao chuyên đề chữ số tận cùng. Hôm nay. Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp xét dãy số phụ như sau:

                                 Giải

C =  1 x 6 + 6 x 11 + 11 x 16+ 16 x 21 + ... + 2011 x 2016

Xét thừa số thứ nhất của các số hạng có trong tổng C lần lượt là các số thuộc dãy số sau:

1; 6; 11; 16; ...; 2011

Dãy số trên là dãy số cách đều với khoảng cách là: 6 - 1 = 5 

Số số hạng của dãy số trên là: (2011 - 1) : 5 + 1 = 403 (số) (1)

Tích của thừa số có tận cùng bằng 1 với thừa số có tận cùng bằng 6 luôn có tận cùng là 6 (2)

Kết hợp (1) và (2) ta có: Chữ số tận cùng của C là chữ số tận cùng của tổng của 403 số có tận cùng là 6

Vậy C có chữ số tận cùng bằng với chữ số tận cùng của B trong đó:

B =  6 x 403 

B = 2418

Vậy C có chữ số tận cùng là 8

Đáp số: 8

Ta có:

\(x>x-2\)

Để \(x\left(x-2\right)\) thì \(x>0\) và \(x-2< 0\)

*) \(x-2< 0\)

\(x< 0+2\)

\(x< 2\)

Vậy \(0< x< 2\) thì \(x\left(x-2\right)< 0\)

x(x-2)<0 (*)

nhận xét: Với mọi số thực x, ta luôn có: x>x-2

(*) xảy ra khi: x-2<0 và x>0

→ x<2 và x>0

→0<x<2

Vậy 0<x<2