Tìm số tự nhiên n để Phân số B =\(\frac{10n-3}{4n-10}\)đạt giá trị lớn nhất . Tìm giá trị lớn nhất đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(n+3\) là bội của \(n-5\)
\(\Rightarrow n+3⋮n-5\)
\(\Rightarrow\frac{n+3}{n-5}\in Z\)
\(\frac{n+3}{n-5}=\frac{n-5+8}{n-5}=1+\frac{8}{n-5}\)
để \(\frac{n+3}{n-5}\in Z\Rightarrow1+\frac{8}{n-5}\in Z\)
\(\Rightarrow\frac{8}{n-5}\in Z\Rightarrow8⋮n-5\Rightarrow n-5\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
ta có bảng sau:
| n-5 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | 6 | 4 | 7 | 3 | 9 | 1 | 13 | -3 |
| thử lại | TM | TM | TM | TM | TM | TM | TM | TM |
vậy \(n\in\left\{6;4;7;3;9;1;13;-3\right\}\)


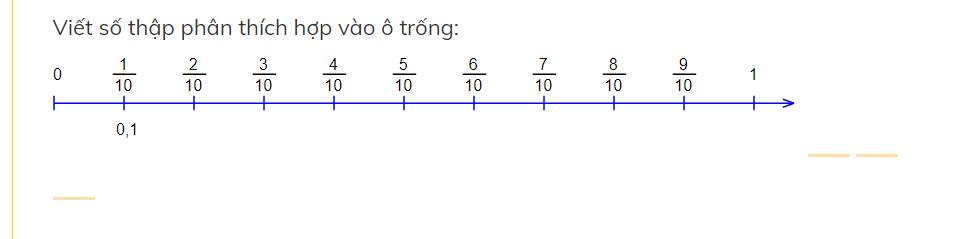
\(\frac{2}{10}=0,2\)
\(\frac{3}{10}=0,3\)
\(\frac{4}{10}=0,1\)
\(\frac{5}{10}=0,5\)
\(\frac{6}{10}=0,6\)
\(\frac{7}{10}=0,7\)
\(\frac{8}{10}=0,8\) Mik ko viết đc tia nên mong bạn thông cảm
\(\frac{9}{10}=0,9\)
\(1=1,1\)


a) \(\frac{3}{4}-1\frac{1}{2}+0,5\div\frac{5}{12}=\frac{3}{4}-\frac{3}{2}+\frac{6}{5}=\frac{9}{20}\)
b) \(\left(-2\right)^2-1\frac{5}{27}\left(-\frac{3}{2}\right)^3=4-\frac{32}{27}.\frac{27}{8}=4-4=0\)
c) \(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{99.100}\)
\(=\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+...+\frac{100-99}{99.100}\)
\(=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{100}\)
\(=\frac{1}{2}-\frac{1}{100}=\frac{49}{100}\)



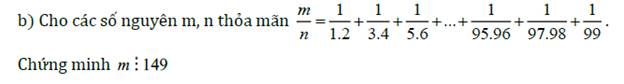
ta có:\(B=\frac{10n-3}{4n-10}=\frac{5.\left(2n-5\right)+22}{2.\left(2n-5\right)}=\frac{5}{2}+\frac{22}{2.\left(2n-5\right)}=\frac{5}{2}+\frac{11}{2n-5}\)
\(Bmax\Leftrightarrow\frac{5}{2}+\frac{11}{2n-5}max\Leftrightarrow\frac{11}{2n-5}max\Leftrightarrow2n-5=1\)
\(\Leftrightarrow2n=6\Leftrightarrow n=3\)
\(B=\frac{5}{2}+11=\frac{27}{2}\)
VẬY \(n=3\) THÌ \(maxB=\frac{27}{2}\)