a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>HB=HC

=>H là trung điểm của CB

Xét ΔCBN có

CM là đường trung tuyến

\(CI=\dfrac{2}{3}CM\)

Do đó: I là trọng tâm của ΔCBN

Xét ΔCBN có

I là trọng tâm

H là trung điểm của BC

Do đó: I,N,H thẳng hàng

skibidi toillet nhé 

a: Xét ΔBAI vuông tại A và ΔBMI vuông tại M có

BI chung

\(\widehat{ABI}=\widehat{MBI}\)

Do đó: ΔBAI=ΔBMI

=>IA=IM

=>ΔIAM cân tại I

 b: Xét ΔBNC có

NM,CA là các đường cao

NM cắt CA tại I

Do đó: I là trực tâm của ΔBNC

=>BI\(\perp\)NC

c: Sửa đề: Chứng minh AM//NC

Xét ΔBMN vuông tại M và ΔBAC vuông tại A có

BM=BA(ΔBMI=ΔBAI)

\(\widehat{MBN}\) chung

Do đó: ΔBMN=ΔBAC

=>BN=BC

Xét ΔBNC có \(\dfrac{BA}{BN}=\dfrac{BM}{BC}\)

nên AM//NC

x = 3

\(\dfrac{6}{x}=\dfrac{10}{5}\)

=>\(x=6\cdot\dfrac{5}{10}\)

=>\(x=\dfrac{30}{10}=3\)

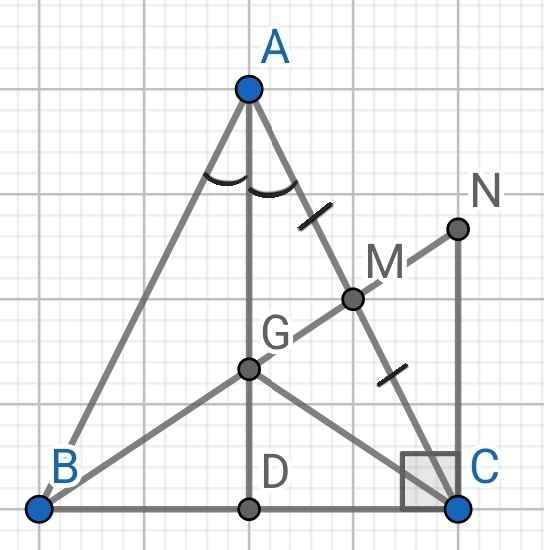
a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC

b) ∆ABC cân tại A (gt)

AD đường tia phân giác (gt)

⇒ AD cũng là đường trung tuyến

Lại có:

BM là đường trung tuyến của ∆ABC (gt)

BM cắt AD tại G (gt)

⇒ G là trọng tâm của ∆ABC

⇒ BG = 2GM

Do BM là đường trung tuyến của ∆ABC (gt)

⇒ M là trung điểm của AC

⇒ AM = CM

Do CN ⊥ BC (gt)

AD ⊥ BC (cmt)

⇒ CN // AD

⇒ ∠CNM = ∠AGM (so le trong)

Xét ∆CMN và ∆AMG có:

∠CNM = ∠AGM (cmt)

∠CMN = ∠AMG (đối đỉnh)

CM = AM (cmt)

⇒ ∆CMN = ∆AMG (g-c-g)

⇒ MN = MG (hai cạnh tương ứng)

⇒ GN = 2GM

Mà BG = 2GM (cmt)

⇒ BG = GN

c) Do AD là đường trung tuyến của ∆ABC (cmt)

⇒ D là trung điểm của BC

⇒ BD = CD

Xét hai tam giác vuông: ∆GDB và ∆GDC có:

GD là cạnh chung

BD = CD (cmt)

⇒ ∆GDB = ∆GDC (hai cạnh góc vuông)

⇒ BG = CG (hai cạnh tương ứng)

Mà BG = GN (cmt)

⇒ GN = CG

⇒ ∆GNC cân tại G

Để ∆GNC đều thì ∠GNC = 60⁰

Mà CN // AD (cmt)

⇒ ∠GNC = ∠AGM = 60⁰ (so le trong)

⇒ ∠MAG = 90⁰ - 60⁰ = 30⁰

⇒ ∠CAD = 30⁰

⇒ ∠BAD = ∠CAD = 30⁰

⇒ ∠BAC = ∠BAD + ∠CAD = 30⁰ + 30⁰ = 60⁰

Mà ∆ABC cân (gt)

⇒ ∆ABC đều

Vậy ∆ABC đều thì ∆GNC đều

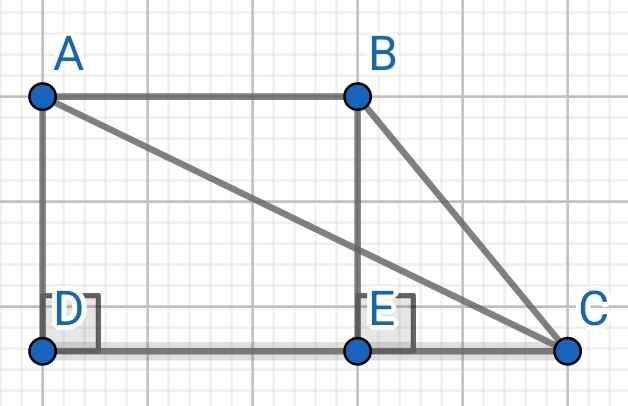
a) ∆ADC vuông tại D

⇒ AC² = AD² + CD² (Pythagore)

⇒ AD² = AC² - CD²

= 17² - 15²

= 64

⇒ AD = 8 (cm)

Kẻ BE ⊥ CD

⇒ BE ⊥ AB

⇒ ∠ABE = ∠BED = ∠ADE = ∠BAD = 90⁰

⇒ ABED là hình chữ nhật

⇒ BE = AD = 8 (cm)

⇒ DE = AB = 9 (cm)

⇒ CE = CD - DE

= 15 - 9

= 6 (cm)

∆BEC vuông tại E

⇒ BC² = BE² + CE² (Pythagore)

= 8² + 6²

= 100

⇒ BC = 10 (cm)

Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

=>\(\widehat{BDA}=\widehat{BDE}\)

mà \(\widehat{BDA}=\widehat{DBK}\)(BK//AC)

nên \(\widehat{KBD}=\widehat{KDB}\)

=>ΔKBD cân tại K

giúp mình với mình đang gấp

Lời giải:

a.

$A(x)=(-9x^4+9x^4)+(-5x^3+4x^3)+6x^2-11x+6$

$=-x^3+6x^2-11x+6$

Bậc của $A(x)$ là $3$

b.

$B(-2)=(-2+3)A(-2)=A(-2)=-(-2)^3+6(-2)^2-11(-2)+6=60$

c.

$A(x):(x-3)=(-x^3+6x^2-11x+6):(x-3)=[-x^2(x-3)+3x(x-3)-2(x-3)]:(x-3)$
$=(x-3)(-x^2+3x-2):(x-3)=-x^2+3x-2$

giup minh voi

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔABD=ΔEBD

b: Ta có: BK//AC

=>\(\widehat{DBK}=\widehat{BDA}\)(hai góc so le trong)

mà \(\widehat{BDA}=\widehat{BDE}\)(ΔBDA=ΔBDE)

nên \(\widehat{KBD}=\widehat{KDB}\)

=>ΔKBD cân tại K

Ta có:ΔBAD=ΔBED

=> AD=DE

mà DE<DC(ΔDEC vuông tại E)

nên DA<DC

c: Sửa đề; Chứng minh B,D,M thẳng hàng

Xét ΔDAI vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADI}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAI=ΔDEC

=>DI=DC

=>D nằm trên đường trung trực của IC(1)

Ta có: ΔDAI=ΔDEC
=>AI=EC

Ta có: BA+AI=BI

BE+EC=BC

mà BA=BE và AI=EC

nên BI=BC

=>B nằm trên đường trung trực của IC(2)

ta có:MI=MC

=>M nằm trên đường trung trực của IC(3)

Từ (1),(2),(3) suy ra B,D,M thẳng hàng

?