
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình bạn tự vẽ nhé, tại trên này chưa cho duyệt hình.
Ta thấy \(\widehat{BAQ}=\widehat{QCA}\) do chúng cùng phụ với \(\widehat{ABC}\)
Lại có \(\widehat{QAN}=\widehat{NAC}\) (do AN là phân giác của \(\widehat{QAC}\))
\(\Rightarrow\widehat{BAQ}+\widehat{QAN}=\widehat{QCA}+\widehat{NAC}\)
\(\Rightarrow\widehat{BAN}=\widehat{BNA}\) (vì \(\widehat{BNA}\) lá góc ngoài của tại N tam giác ACN)
\(\Rightarrow\Delta BAN\) cân tại B
Vì BK là đường cao của tam giác BAN cân tại B nên BK cũng là đường trung trực của tam giác BAN.
Lại có \(I\in BK\) nên \(IN=IA\).
Tương tự, ta cũng có \(IM=IA\) \(\Rightarrow IM=IN\left(=IA\right)\)
\(\Rightarrow\Delta IMN\) cân tại I (1)
Kéo dài tia AI và đặt là Ax. Khi đó \(\widehat{MIx}=\widehat{IAM}+\widehat{IMA}\) (do \(\widehat{MIx}\) là góc ngoài tại I của tam giác IAM) \(=2\widehat{MAx}\) (vì tam giác IAM cân tại I nên \(\widehat{IAM}=\widehat{IMA}\))
Tương tự, ta có \(\widehat{NIx}=2\widehat{NAx}\)
\(\Rightarrow\widehat{MIx}+\widehat{NIx}=2\left(\widehat{MAx}+\widehat{NAx}\right)\)
\(\Rightarrow\widehat{MIN}=2\widehat{MAN}\)
Mà \(\widehat{MAN}=\widehat{MAQ}+\widehat{NAQ}=\dfrac{1}{2}\left(\widehat{BAQ}+\widehat{CAQ}\right)=\dfrac{1}{2}\widehat{BAC}=45^o\)
Nên \(\widehat{MIN}=2.45^o=90^o\) (2)
Từ (1) và (2) \(\Rightarrow\Delta IMN\) vuông cân tại I (đpcm)

- 1,25 = \(\dfrac{-125}{100}\) = \(\dfrac{-125:25}{100:25}\) = \(\dfrac{-5}{4}\)

\(f\left(x\right)⋮g\left(x\right)\)
=>\(-2x^3-7x^2-5x+5⋮x+2\)
=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)

a: VT=\(\left(a+1\right)\left(a^2-a+1\right)\)
\(=a^3-a^2+a+a^2-a+1\)
\(=a^3+1\)=VP
b: \(VT=\left(a+1\right)\left(a^3-a^2+a-1\right)\)
\(=a^4-a^3+a^2-a+a^3-a^2+a-1\)
\(=a^4-1=VP\)

\(f\left(x\right)⋮g\left(x\right)\)
=>\(2x^2-x+2⋮2x+1\)
=>\(2x^2+x-2x-1+3⋮2x+1\)
=>\(3⋮2x+1\)
=>\(2x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-1;1;-2\right\}\)

1: \(\left(x-\dfrac{1}{2}\right)^2>=0\forall x\)
=>\(A=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
2: \(\left|3x-1\right|>=0\forall x\)
=>\(\left|3x-1\right|-5>=-5\forall x\)
Dấu '=' xảy ra khi 3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)
3: \(\left(2-x\right)^2>=0\forall x\)
=>\(-\left(2-x\right)^2< =0\forall x\)
=>\(C=-\left(2-x\right)^2+5< =5\forall x\)
Dấu '=' xảy ra khi 2-x=0
=>x=2
4: \(\left(x^2-4\right)^2>=0\forall x\)
\(\left|y-x\right|>=0\forall x,y\)
Do đó: \(\left(x^2-4\right)^2+\left|y-x\right|>=0\forall x,y\)
=>\(D=\left(x^2-4\right)^2+\left|y-x\right|+3>=3\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2-4=0\\y-x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y=x\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y=x=2\\y=x=-2\end{matrix}\right.\)
5: \(\left(x-1\right)^2>=0\forall x\)
\(\left(x^2-1\right)^4>=0\forall x\)
Do đó: \(E=\left(x-1\right)^2+\left(x^2-1\right)^4>=0\forall x\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\x^2-1=0\end{matrix}\right.\)
=>x=1
6: \(\left(x+3\right)^2+3>=3\forall x\)
=>\(F=\dfrac{2}{\left(x+3\right)^2+3}< =\dfrac{2}{3}\forall x\)
Dấu '=' xảy ra khi x+3=0
=>x=-3
7: \(\left(x^2+1\right)^2>=1^2=1\forall x\)
=>\(\left(x^2+1\right)^2+2022>=2023\forall x\)
=>\(G=\dfrac{2023}{\left(x^2+1\right)^2+2022}< =\dfrac{2023}{2023}=1\forall x\)
Dấu '=' xảy ra khi x=0

Còn phụ thuộc vào nhiều yếu tố phụ kèm theo nữa em nhé.
+ Hạnh kiểm tốt
+ Không có môn nào dưới 6,5
....

Lời giải:
$P(1)=1^{2024}+1^{2023}+....+1+1P(1)$
$=\underbrace{1+1+...+1}_{2024}+P(1)=2024+P(1)$
$\Rightarrow 2024=0$ (vô lý)
Vậy không tồn tại $P(x)$ thỏa mãn đề.
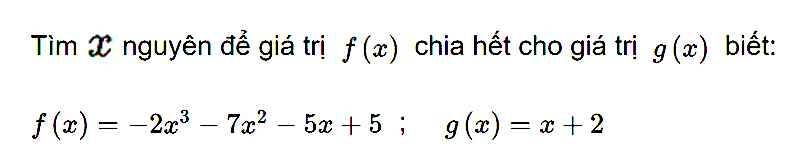
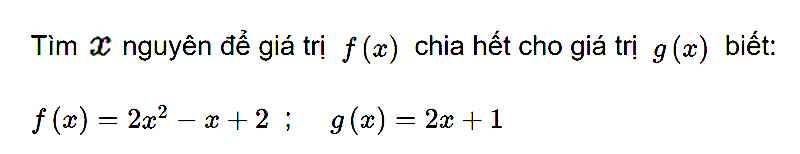
\(x^3+x^2-x+a⋮x^2+2x+1\)
=>\(x^3+2x^2+x-x^2-2x-1+a+1⋮x^2+2x+1\)
=>a+1=0
=>a=-1