Bạn Mai có một hộp bút đựng hai chiếc bút màu xanh và 1 chiếc bít màu đỏ. Bạn Mai lấy ngẫu nhiên một chiếc bút từ hợp cho bạn Huy mượn. Xét các biến cố sau:
A: “Mai lấy được chiếc bút màu đỏ":
B: "Mai lấy được chiếc bút màu xanh".
C: “Mai lấy được chiếc bút màu đen".
“Mai lấy được chiếc bút màu đỏ hoặc màu xanh".
a) Trong các biến cổ trên, hãy chỉ ra biến cố không thể, biến cố chắc chắn.
b) Tính xác suất của biến cố ngẫu nhiên có trong các biến cố trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\left(\dfrac{1}{2^2}-1\right)\cdot\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{1000^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\cdot\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{1000}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{1000}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-999}{1000}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot....\cdot\dfrac{1001}{1000}\)
\(=\dfrac{-1}{1000}\cdot\dfrac{1001}{2}=\dfrac{-1001}{2000}\)

Bài 3:
a: \(3\in N;3\in Z;3\in Q\)
b: \(10\in N;10\in Z;10\in Q\)
c: \(-\dfrac{3}{7}\in Q\)
d: \(-2\in Z;-2\in Q\)
Bài 2:
\(\dfrac{-3}{5}=\dfrac{-27}{45};\dfrac{-5}{9}=\dfrac{-25}{45};-1\dfrac{2}{3}=\dfrac{-5}{3}=\dfrac{-75}{45};0,5=\dfrac{22,5}{45};\dfrac{10}{9}=\dfrac{50}{45}\)
mà -75<-27<-25<22,5<50
nên \(-1\dfrac{2}{3}< -\dfrac{3}{5}< -\dfrac{5}{9}< \dfrac{1}{2}< \dfrac{10}{9}\)
Bài 1:
a: \(\dfrac{9}{70}=\dfrac{9\cdot3}{70\cdot3}=\dfrac{27}{210};\dfrac{5}{42}=\dfrac{5\cdot5}{42\cdot5}=\dfrac{25}{210}\)
mà 27>25
nên \(\dfrac{9}{70}>\dfrac{5}{42}\)
b: \(\dfrac{-4}{27}=\dfrac{-4\cdot7}{27\cdot7}=\dfrac{-28}{189};\dfrac{10}{-63}=\dfrac{-10}{63}=\dfrac{-10\cdot3}{63\cdot3}=\dfrac{-30}{189}\)
mà -28>-30
nên \(\dfrac{-4}{27}>\dfrac{10}{-63}\)
c: \(\dfrac{999}{556}=1+\dfrac{443}{556};\dfrac{1000}{557}=1+\dfrac{443}{557}\)
mà \(\dfrac{443}{556}>\dfrac{443}{557}\)
nên \(\dfrac{999}{556}>\dfrac{1000}{557}\)
d: \(\dfrac{-2}{15}< 0;\dfrac{-10}{-11}=\dfrac{10}{11}>0\)
Do đó: \(\dfrac{-2}{15}< \dfrac{-10}{-11}\)

a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>\(\widehat{MAC}=\widehat{MDB}\)
=>AC//DB
mà AC\(\perp\)AB
nên BD\(\perp\)BA
c: Xét ΔCAB vuông tại A và ΔDBA vuông tại B có
BA chung
AC=BD
Do đó: ΔCAB=ΔDBA
=>CB=DA
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}CB\)

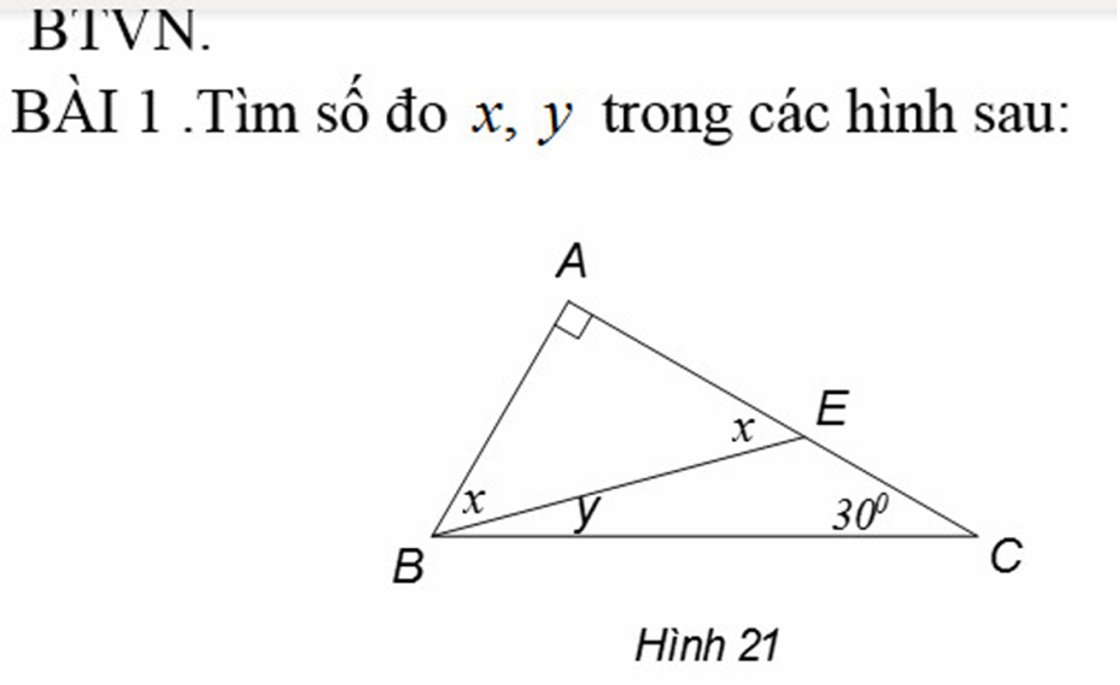
Xét ΔABE có: \(\widehat{BAE}+\widehat{ABE}+\widehat{AEB}=180^o\)
\(\Rightarrow90^o+x+x=180^o\Rightarrow2x=180^o-90^o=90^o\)
\(\Rightarrow x=\dfrac{90^o}{2}=45^o\)
Xét ΔABC có: \(\widehat{ABC}+\widehat{BAC}+\widehat{CAB}=180^o\)
\(\Rightarrow\left(x+y\right)+90^o+30^o=180^o\)
\(\Rightarrow\left(x+y\right)+120^o=180^o\)
\(\Rightarrow45^o+y=180^o-120^o\)
\(\Rightarrow45^o+y=60^o\)
\(\Rightarrow y=60^o-45^o=15^o\)
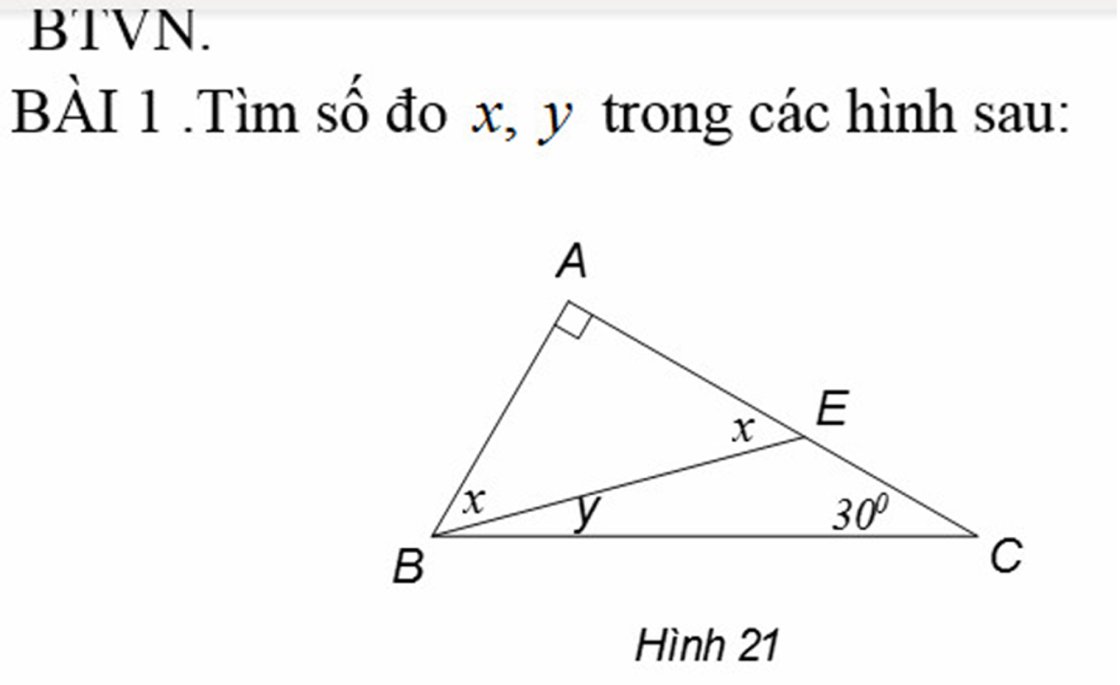
∆ABE vuông tại A (gt)
⇒ ∠ABE + ∠AEB = 90⁰
⇒ x + x = 90⁰
⇒ x = 90⁰ : 2
= 45⁰
∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠ACB = 90⁰
⇒ ∠ABC = 90⁰ - ∠ACB
= 90⁰ - 30⁰
= 60⁰
⇒ y = ∠ABC - x
= 60⁰ - 45⁰
= 15⁰

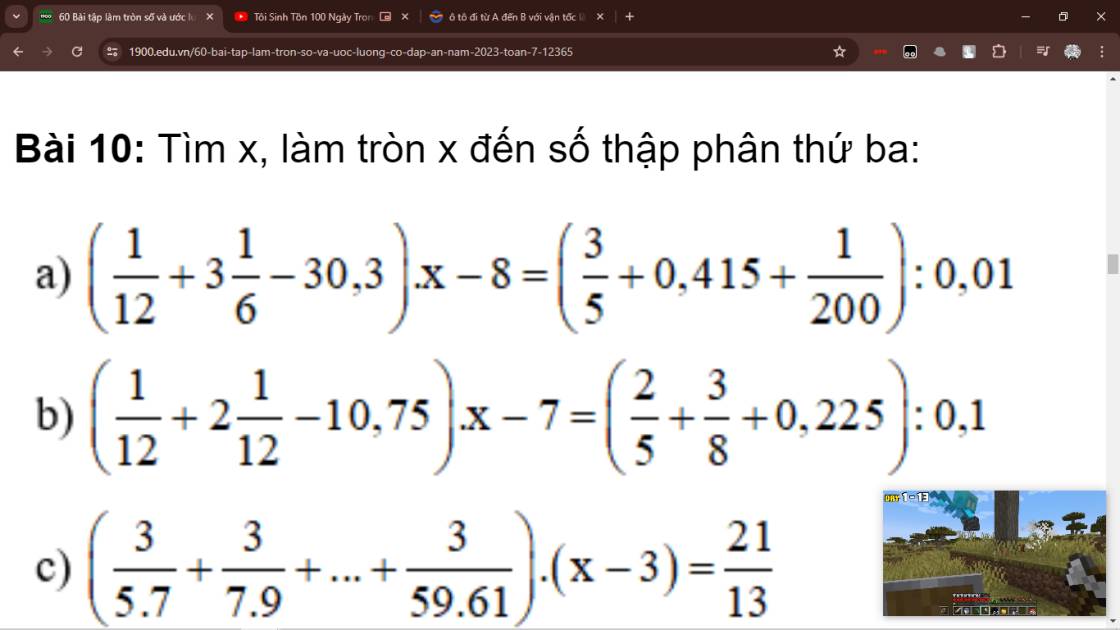
a)
\(\left(\dfrac{1}{12}+3\dfrac{1}{6}-30,3\right)x-8=\left(\dfrac{3}{5}+0,415+\dfrac{1}{200}\right):0,01\\ \Rightarrow\left(\dfrac{1}{12}+\dfrac{19}{6}-\dfrac{303}{10}\right)x-8=\left(\dfrac{3}{5}+0,415+\dfrac{1}{200}\right)\cdot100\\ \Rightarrow-\dfrac{541}{20}x-8=\dfrac{51}{50}\cdot100\\ \Rightarrow-\dfrac{541}{20}x-8=102\\ \Rightarrow-\dfrac{541}{20}x=110\\ \Rightarrow x=110:-\dfrac{541}{20}\\\Rightarrow x=-\dfrac{2200}{541}\approx4,067\)
b)
\(\left(\dfrac{1}{12}+2\dfrac{1}{12}-10,75\right)x-7=\left(\dfrac{2}{5}+\dfrac{3}{8}+0,225\right):0,1\\ \Rightarrow\left(\dfrac{1}{12}+\dfrac{25}{12}-\dfrac{43}{4}\right)x-7=\left(\dfrac{2}{5}+\dfrac{3}{8}+\dfrac{9}{40}\right)\cdot10\\ \Rightarrow-\dfrac{103}{12}x=1\cdot10\\ \Rightarrow x=10:-\dfrac{103}{12}\\ \Rightarrow x=-\dfrac{120}{103}\\ \Rightarrow x\approx-1,165\)
c)
\(\left(\dfrac{3}{5\cdot7}+\dfrac{3}{7\cdot9}+...+\dfrac{3}{59\cdot61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{59\cdot61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\right)\left(x-3\right)=\dfrac{21}{13}\\\Rightarrow \dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{84}{305}\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow x-3=\dfrac{21}{13}:\dfrac{84}{305}\\ \Rightarrow x-3=\dfrac{305}{52}\\ \Rightarrow x=\dfrac{305}{52}+3\\ \Rightarrow x=\dfrac{461}{52}\\ \Rightarrow x\approx8,865\)

Bài 10:
\(A=\dfrac{2^{12}\cdot3^5-4^6\cdot81}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}\\ =\dfrac{2^{12}\cdot3^5-\left(2^2\right)^6\cdot3^4}{\left(2^2\right)^6\cdot3^6+\left(2^3\right)^4\cdot3^5}\\ =\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^6+2^{12}\cdot3^5}\\ =\dfrac{2^{12}\cdot3^4\cdot\left(3-1\right)}{2^{12}\cdot3^5\cdot\left(3+1\right)}\\ =\dfrac{3-1}{3\cdot\left(3+1\right)}\\ =\dfrac{2}{3\cdot4}\\ =\dfrac{1}{6}\)
\(B=\dfrac{30\cdot4^7\cdot3^{29}-5\cdot14^5\cdot2^{12}}{54\cdot6^{14}\cdot9^7-12\cdot8^5\cdot7^5}\\ =\dfrac{2\cdot3\cdot5\cdot\left(2^2\right)^7\cdot3^{29}-5\cdot2^5\cdot7^5\cdot2^{12}}{2\cdot3^3\cdot2^{14}\cdot3^{14}\cdot\left(3^2\right)^7-2^2\cdot3\cdot\left(2^3\right)^5\cdot7^5\cdot}\\ =\dfrac{3^{30}\cdot2^{15}\cdot5-5\cdot2^{17}\cdot7^5}{2^{15}\cdot3^{17}\cdot3^{14}-2^{17}\cdot7^5\cdot3}\\ =\dfrac{3^{30}\cdot2^{15}\cdot5-5\cdot2^{17}\cdot7^5}{2^{15}\cdot3^{31}-2^{17}\cdot7^5\cdot3}\\ =\dfrac{5\cdot\left(3^{30}\cdot2^{15}-2^{17}\cdot7^5\right)}{3\cdot\left(2^{15}\cdot3^{30}-2^{17}\cdot7^5\right)}\\ =\dfrac{5}{3}\)
Bài 8:
\(\left\{{}\begin{matrix}x+y=\dfrac{1}{2}\\y+z=\dfrac{1}{3}\\x+z=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{3}-z+\dfrac{1}{6}-z=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}-2z=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2z=0\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}z=0\\y=\dfrac{1}{3}-0=\dfrac{1}{3}\\x=\dfrac{1}{6}-0=\dfrac{1}{6}\end{matrix}\right.\)
Bài 5:
\(A=\left(\dfrac{3}{2}-\dfrac{2}{5}+\dfrac{1}{10}\right):\left(\dfrac{3}{2}-\dfrac{2}{3}+\dfrac{1}{12}\right)\)
\(=\dfrac{15-4+1}{10}:\dfrac{9-4+1}{12}\)
\(=\dfrac{12}{10}\cdot\dfrac{12}{6}=\dfrac{6}{5}\cdot2=\dfrac{12}{5}\)

\(S=1+2+2^2+2^3+...+2^{2009}+2^{2008}\\ 2S=2\left(1+2+2^2+...+2^{2008}\right)\\ 2S=2+2^2+2^3+...+2^{2009}\\ 2S-S=\left(2+2^2+2^3+...+2^{2009}\right)-\left(1+2+2^2+...+2^{2008}\right)\\ S=2^{2009}-1\)

\(-\dfrac{25}{20}>0\)
\(\dfrac{20}{25}>0\)
\(\Rightarrow-\dfrac{25}{20}< \dfrac{20}{25}\)

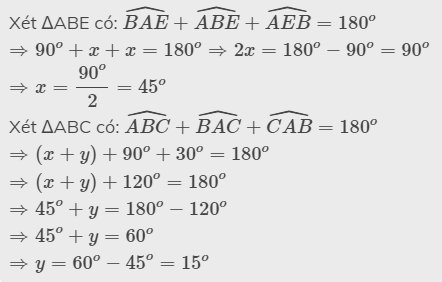



a: Các biến cố không thể là C
Biến cố chắc chắn là D
b: Biến cố ngẫu nhiên là A,B
A: "Mai lấy được bút màu đỏ"
n(A)=1
\(P_A=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{3}\)
B: "Mai lấy được bút màu xanh"
=>n(B)=2
=>\(P_B=\dfrac{n\left(B\right)}{n\left(\Omega\right)}=\dfrac{2}{3}\)
tk ạ
a) Biến cố không thể là C: "Mai lấy được chiếc bút màu đen", vì trong hộp chỉ có hai chiếc bút màu xanh và một chiếc bút màu đỏ.
Biến cố chắc chắn là "Mai lấy được chiếc bút màu đỏ hoặc màu xanh", vì không có trường hợp nào khác xảy ra.
b) Xác suất của các biến cố:
P(A) = 1/3 (vì trong hộp có một chiếc bút màu đỏ và hai chiếc bút màu xanh)
P(B) = 2/3
P(C) = 0
P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 1/3 + 2/3 - 0 = 1
Chú ý rằng P(A ∪ B) là biến cố "Mai lấy được chiếc bút màu đỏ hoặc màu xanh", và P(A ∩ B) = 0 vì không thể lấy được cả hai chiếc bút cùng lúc.