cho f(X) =(x-4)-3(x+1). Tìm x sao cho f(x)=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



P - Q + R =(2x2 - 3xy + 4y2) - (3x2 + 4xy -y2) + (x2 +2xy +3y2)
= 2x2 - 3xy + 4y2 - 3x2 - 4xy + y2 + x2 + 2xy + 3y2
=(2x2 - 3x2 + x2) + ( -3xy - 4xy +2xy) + (4y2 + y2 +3y2)
= -5xy + 8y2
Vậy P - Q + R = - 5xy + 8y2
Bài 5:
\(P-Q+R=\) \(\left(2x^2-3xy+4y^2\right)-\left(3x^2+4xy-y^2\right)+\left(x^2+xy+3y^2\right)\)
\(P-Q+R=\) \(2x^2-3xy+4y^2-3x^2-4xy+y^2+x^2+xy+3y^2\)
\(P-Q-R=\) \(\left(2x^2-3x^2+x^2\right)+\left(-3xy-4xy+2xy\right)+\left(4y^2+y^2+2y^2\right)\)
\(P-Q-R=\) \(0-5xy+7y^2\)
Vậy \(P-Q-R=\) \(-5xy+7y^2\)

a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC

a) Theo bất đẳng thức tam giác, ta có:
\(AC-BC< AB< AC+BC\Rightarrow8-1< AB< 8+1\)
\(\Rightarrow7< AB< 9\) mà độ dài cạnh \(AB\) là số nguyên
\(\Rightarrow AB=8\left(cm\right)\Rightarrow AB=AC\Rightarrow\Delta ABC\) cân tại \(A\)
b) (Tự vẽ hình)
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(\widehat{B}=\widehat{C}\) (do \(\Delta ABC\) cân)
\(AB=AC=8\left(cm\right)\)
\(\widehat{BAM}=\widehat{CAM}\) (tính chất phân giác)
\(\Rightarrow\Delta ABM=\Delta ACM\) (g.c.g)


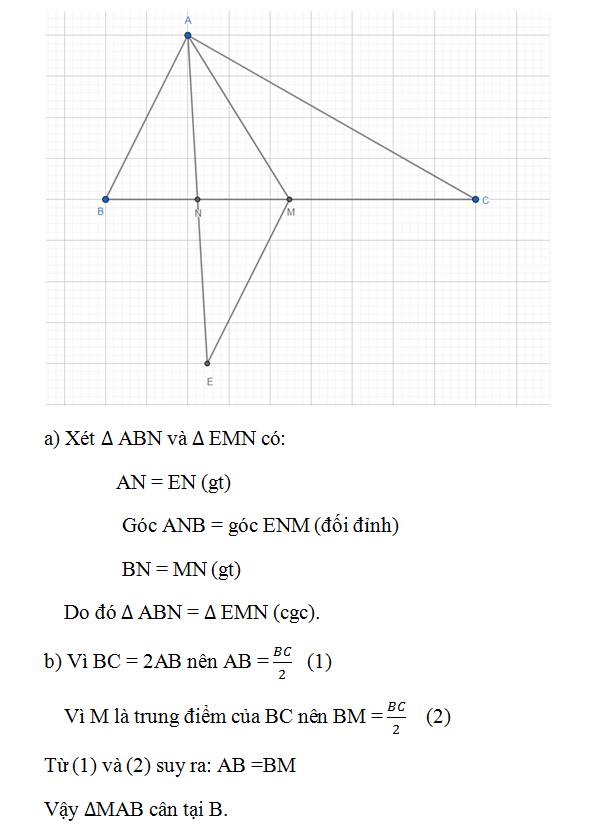
 giúp mik câu 4
giúp mik câu 4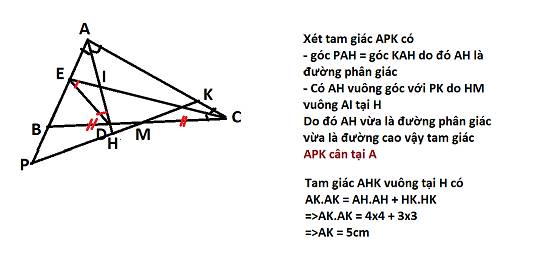
Ta có: f \(\left(x\right)=4\)
hay\(\left(x-4\right)-3\left(x+1\right)=4\)
\(x-4-3x-1.3=4\)
\(x-4-3x-3=4\)
\(x-3x\) \(=4+4+3\)
\(1x-3x\) \(=11\)
\(-2x\) \(=11\)
\(x\) \(=11:\left(-2\right)\)
\(x\) \(=-\dfrac{11}{2}\)
Vậy \(x=-\dfrac{11}{2}\)