PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 11 2021
Với \(n=0\Rightarrow0-0+0-0+0-0=0⋮24\left(đúng\right)\)
Với \(n=1\Rightarrow1-3+6-7+5-2=0⋮24\left(đúng\right)\)
G/s \(n=k\Rightarrow\left(k^6-3k^5+6k^4-7k^3+5k^2-2k\right)⋮24\)
\(\Rightarrow k\left(k^5-3k^4+6k^3-7k^2+5k-2\right)⋮24\\ \Rightarrow k\left(k+1\right)\left(k^2+k+1\right)\left(k^2-k+2\right)⋮24\)
Với \(n=k+1\), ta cần cm \(\left[\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\right]⋮24\)
Ta có \(\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\)
\(=\left(k+1\right)\left[\left(k+1\right)^5-3\left(k+1\right)^4+6\left(k+1\right)^3-7\left(k+1\right)+5\left(k+1\right)-2\right]\\ =\left(k+1\right)\left(k+1-1\right)\left[\left(k+1\right)^2-\left(k+1\right)+1\right]\left[\left(k+1\right)^2-\left(k+1\right)+2\right]\\ =k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)\)
Mà theo GT quy nạp ta có \(k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)⋮24\)
Vậy ta được đpcm
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2021
\(n=1\Rightarrow1^1\ge1!\) đúng
Giả sử đúng với \(n=k\) hay \(k^k\ge k!\)
Cần chứng minh đúng với \(n=k+1\) hay \(\left(k+1\right)^{k+1}\ge\left(k+1\right)!\)
Ta có:
\(\left(k+1\right)^{k+1}=\left(k+1\right).\left(k+1\right)^k>\left(k+1\right).k^k\ge\left(k+1\right).k!=\left(k+1\right)!\) (đpcm)
5 tháng 10 2021
thầy cho em hỏi đáp án cuat thầy là của bài
Sử dụng phương pháp quy nạp toán học, chứng minh:
Với n nguyên dương, chứng minh n! ≤nn
đúng không ạ em cảm ơn thầy
30 tháng 6 2019
Dễ thấy dấu"=" xảy ra khi x=1
Giả sử bđt đúng với n=k>1 tức là
\(3^k\ge2k+1\) (1)
Nhân cả 2 vế của (1) với 3 ta được
\(3^{k+1}\ge6k+3\Leftrightarrow3^{k+1}\ge3k+4+3k-1\)
Vì 3k-1>0
=>\(3^{k+1}\ge3\left(k+1\right)+1\)
Vậy bđt đúng với n=k+1
=> bđt được chứng minh
PT
1
CM
23 tháng 5 2019
Hàm số cho bằng bảng
Ví dụ:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
- Hàm số cho bằng công thức:
Ví dụ:
PT
1
CM
12 tháng 1 2019
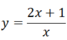
* Với n =1 ta có 1 3 + 11.1 = 12 chia hết cho 6 đúng.
* Giả sử với n = k thì k 3 + 11 k chia hết cho 6.
* Ta phải chứng minh với n =k+1 thì ( k + 1 ) 3 + 11(k +1) chia hết cho 6.
Thật vậy ta có :
k + 1 3 + 11 k + 1 = k 3 + 3 k 2 + 3 k + 1 + 11 k + 11 = ( k 3 + 11 k ) + 3 k ( k + 1 ) + 12 *
Ta có; k 3 +11k chia hết cho 6 theo bước 2.
k(k+1) là tích 2 số tự nhiên liên tiếp nên chia hết cho 2 ⇒ 3 k ( k + 1 ) ⋮ 6
Và 12 hiển nhiên chia hết cho 6.
Từ đó suy ra (*) chia hết cho 6 (đpcm).
CM
24 tháng 6 2018
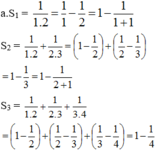
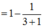
b. Dự đoán: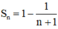 
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
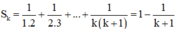
Khi đó:
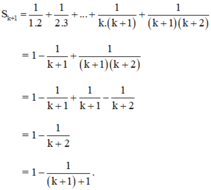
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
+ Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈ N* là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:
Bước 1: Kiểm tra mệnh đề đúng với n = 1 .
Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.
Bước 3: Kết luận mệnh đề đúng với n ∈ N*.
+ Ví dụ: Chứng minh rằng với mọi n ∈ N* ta có: n3 + 5n chia hết cho 6.
Chứng minh: Đặt P(n) = n3 + 5n.
Với n =1 ⇒ P(1) = 6 ⋮ 6
Giả sử (Pn) chia hết cho 6 đúng với n=k ≥1, nghĩa là, ta có:
P(k) = (k3 + 5k) ⋮ 6.
Ta có: P(k+1) = (k+1)3 + 5(k+1) = k3 + 3k2 + 3k + 1 + 5k + 5 = k3 + 5k + 3(k2 + k) + 6
Mặt khác, theo giả thiết quy nạp ta có: k3 + 5k ⋮6.
Hơn nữa k2 + k = k(k+1) : 2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).
Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.
Theo nguyên lí quy nạp, ta có P(n) = n3 + 5n chia hết cho 6 với mọi n ∈ N*.