Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
Bạn ơi bạn chỉ mình cách bình thường được ko? Vì mình chưa học tọa độ hóa.

❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

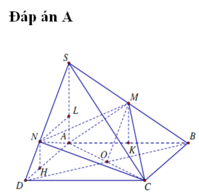
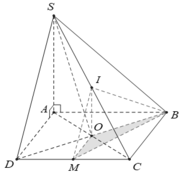
vì (SBI) và (SCI) cùng vuông góc với( ABCD) nên SI vuông với (ABCD) ,ke Az song song với SI và chọn gốc tọa độ tại A

Chọn A.
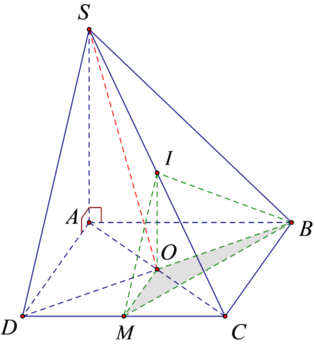
Do IO là đường trung bình của tam giác SAC nên:
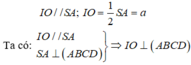
* OM là đường trung bình tam giác ACD nên:
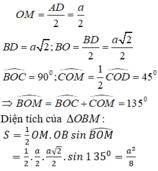
Tính thể tích của khối chóp I.OBM:
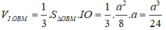
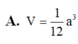
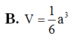
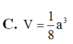
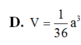

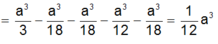
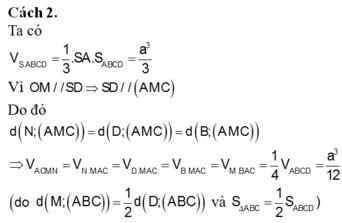

vẽ hình đi bạn