Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho a,b,c,d là các số dương thỏa mãn a^2 + b^2=1 và a^4/c+b^4/d=1/c+d.Chứng minh rằng:a^2/c+d/b^2>=2

Cho a,b,c,d là các số dương thỏa mãn a^2 + b^2=1 và a^4/c+b^4/d=1/c+d.Chứng minh rằng:a^2/c+d/b^2>=2


Câu hỏi của Adminbird - Toán lớp 7 - Học toán với OnlineMath

\(\Sigma_{sym}a^4b^4\ge\frac{\left(\Sigma_{sym}a^2b^2\right)^2}{3}\ge\frac{\left(\Sigma_{sym}ab\right)^4}{27}\ge\frac{a^2b^2c^2\left(a+b+c\right)^2}{3}=3a^4b^4c^4\)
\(\Sigma\frac{a^5}{bc^2}\ge\frac{\left(a^3+b^3+c^3\right)^2}{abc\left(a+b+c\right)}\ge\frac{\left(a^2+b^2+c^2\right)^4}{abc\left(a+b+c\right)^3}\ge\frac{\left(a+b+c\right)^6\left(a^2+b^2+c^2\right)}{27abc\left(a+b+c\right)^3}\)
\(\ge\frac{\left(3\sqrt[3]{abc}\right)^3\left(a^2+b^2+c^2\right)}{27abc}=a^2+b^2+c^2\)
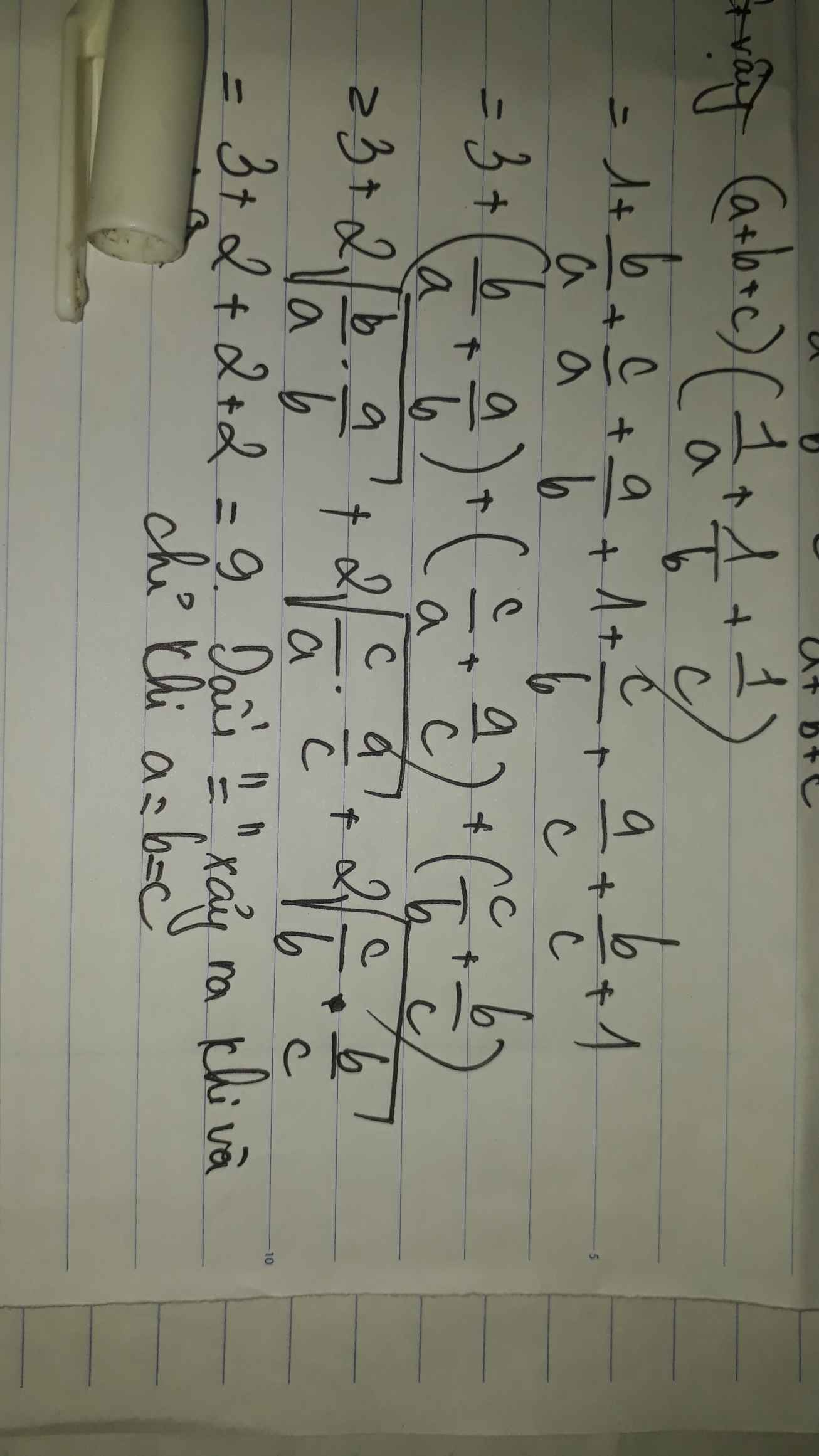
(a+b+c)(1/a+1/b+1/c) = 1+ a/b + a/c + b/a + 1 + b/c + c/a + c/b + 1
= 3 + (a/b+b/a) + (c/a+a/c) + (b/c+c/b) (1)
(ở đây mình sẽ chứng minh a/b + b/a >=2)
có: a/b + b/a - 2 = (a^2 + b^2 - 2ab)/ab = ((a-b)^2)/ab
có: (a-b)^2 >= 0; a,b đều là các số dương => a.b >= 0
vậy a/b + b/a -2 >=0
<=> a/b + b/a >= 2
chứng minh tương tự, ta có (c/a+a/c) >=2, (b/c+c/b) >=2
vậy (1) >= 3 + 2 +2 +2 = 9 (đpcm)