Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Câu 2: Lúc 6h sáng tại 2 địa điểm A và B cùng trên 1 đường thẳng cách nhau 60 km,2 ô tô cùng khởi hành chạy cùng chiều theo hướng từ A đến B. Xe đi từ A có vận tốc 50 km/h,xe đi từ B có vận tốc 30 km/h
a)Xác định thời điểm và vị trí 2 xe gặp nhau
b)Xác định thời điểm và vị trí 2 xe cách nhau 20 km
Giải
a) ( Mình giải theo kiểu phương trình của kỳ 2 nha)
* Gọi quãng đường từ khi xe 1 xuất phát đến khi gặp xe 2 là x (km)
\(\ \Rightarrow\) Quãng đường từ khi xe 2 đi đến khi 2 xe gặp nhau là x-60 (km)
Ta có bởi thời gian của 2 xe xuất phát cùng nhau => t1= t2 =t
mà ta có công thức t=\(\frac{S}{v}\)
Vậy ta có phương trình: t=\(\frac{x}{50}\)=\(\frac{x-60}{30}\)
Giải phương trình ta có
\(\Rightarrow\) 30x=50(x-60)
=> 30x=50x-3000
=>3000=50x-30x (chuyển vế)
=>3000=20x
150=x (km)
=> 2 xe gặp nhau sau khi xe 1 xuất phát 150(km)=> t=\(\frac{S}{v}\)=\(\frac{150}{50}\)=3(h)
b) Có v1-v2 =50-30=20(km/h) ; S1-S2= 20(km)
=> t=\(\frac{S_1-S_2}{v_1-v_2}\)=\(\frac{20}{20}\)=1 (h)
Vậy sau khi gặp nhau 1 h thì 2 xe cách nhau 20km
2 gương phẳng G #Hỏi cộng đồng OLM #Vật lý lớp 8

a/ Gọi t là thời gian hai xe gặp nhau
Quãng đường mà xe gắn máy đã đi là :
S1= V1.(t - 6) = 50.(t-6)
Quãng đường mà ô tô đã đi là :
S2= V2.(t - 7) = 75.(t-7)
Quãng đường tổng cộng mà hai xe đi đến gặp nhau.
AB = S1 + S2
\(\Leftrightarrow\) AB = 50. (t - 6) + 75. (t - 7)
\(\Leftrightarrow\)300 = 50t - 300 + 75t - 525
\(\Leftrightarrow\)125t = 1125
\(\Leftrightarrow\) t = 9 (h)
\(\Leftrightarrow\) S1=50. ( 9 - 6 ) = 150 km
Vậy hai xe gặp nhau lúc 9 h và hai xe gặp nhau tại vị trí cách A: 150km và cách B: 150 km.
b/ Vị trí ban đầu của người đi bộ lúc 7 h.
Quãng đường mà xe gắn mắy đã đi đến thời điểm t = 7h.
AC = S1 = 50.( 7 - 6 ) = 50 km.
Khoảng cách giữa người đi xe gắn máy và người đi ôtô lúc 7 giờ.
CB =AB - AC = 300 - 50 =250km.
Do người đi xe đạp cách đều hai người trên nên:
DB = CD = \(\frac{CB}{2}=\frac{250}{2}=125\). km
Do xe ôtô có vận tốc V2=75km/h > V1 nên người đi xe đạp phải hướng về phía A.
Vì người đi xe đạp luôn cách đều hai người đầu nên họ phải gặp nhau tại điểm G cách B 150km lúc 9 giờ. Nghĩa là thời gian người đi xe đạp đi là:
rt = 9 - 7 = 2giờ
Quãng đường đi được là:
DG = GB - DB = 150 - 125 = 25 km
Vận tốc của người đi xe đạp là.
V3 = \(\frac{DG}{\Delta t}=\frac{25}{2}=12,5\) km/h
Gọi t là thời điểm hai xe gặp nhau.
Quãng đường mà xe gắn máy đã đi:
S1=V1.(t-6)=50.(t-6)
Quãng đường mà ôtô đã đi:
S2=V2.(t-7)=75.(t-7)
Quãng đường tổng cộng mà hai xe đến gặp nhau:
AB=S1+S2
300 = 50.(t-6) + 75.(t-7)
300 = 50.t - 50.6 + 75.t - 75.7
t = 9h
Vậy hai xe gặp nhau lúc 9h
Cách A số km là:
S1= 50. (9-6)=150 km

a)ta có:
thời gian ô tô đi trên quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}\)
thời gian ô tô đi trên đoạn đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của ô tô trên toàn bộ quãng đường là:
\(v_{tb1}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{S}{S\left(\frac{1}{2v_1}+\frac{1}{2v_2}\right)}\)
\(\Leftrightarrow v_{tb1}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{1}{\frac{v_2+v_1}{2v_1v_2}}=\frac{2v_1v_2}{v_1+v_2}\)
b)ta có:
quãng đường ô tô đi được trong nửa thời gian đầu là:
S1=v1t1=\(\frac{v_1t}{2}\)
quãng đường ô tô đi được trong thời gian còn lại là:
S2=v2t2=\(\frac{v_2t}{2}\)
vận tốc trung bình của ô tô là:
\(v_{tb2}=\frac{S_1+S_2}{t}=\frac{\frac{vt_1}{2}+\frac{v_2t}{2}}{t}\)
\(\Leftrightarrow v_{tb2}=\frac{t\left(\frac{v_1}{2}+\frac{v_2}{2}\right)}{t}=\frac{v_1+v_2}{2}\)
c)lấy vtb1-vtb2 ta có:
\(\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-\left(v_1+v_2\right)^2}{2v_1+2v_2}\)
\(=\frac{4v_1v_2-\left(v_1^2+2v_1v_2+v_2^2\right)}{2v_1+2v_2}\)
\(=\frac{-v_1^2+2v_1v_2-v_2^2}{2v_1+2v_2}\)
\(=\frac{-\left(v_1-v_2\right)^2}{2v_1+2v_2}\)
mà (v1-v2)2\(\ge\) 0 nên -(v1-v2)2\(\le\) 0
mà vận tốc ko âm nên 2v1+2v2>0
từ hai điều trên nên ta suy ra vận tốc trung bình tìm được ở câu a) bé hơn câu b)

Áp lực tác dụng lên tấm ván có độ lớn bằng trọng lượng của người: F = P = 10.m
Áp suất của người thứ nhất tác dụng lên tấm ván điện tích S1:
Áp suất của người thứ hai tác dụng lên tấm ván diện tích S2:
Lập tỷ số ta được:
Vậy p2 = 1,44.p1

Thời gian t(s) | Quãng đường đi được s(cm) | Vận tốc v(cm/s) |
Trong hai giây đầu : t1 = 2 | S1 =….5 | V1 = …2,5 |
Trong hai giây tiếp theo : t2 = 2 | S2 =….5 | V2 = …2,5 |
Trong hai giây cuối : t3 = 2 | S3 =….5 | V3 = …2,5 |
Kết luận :
“Một vật đang chuyển động, nếu chịu tác dụng của lực cân bằng thì sẽ tiếp tục chuyển động thẳng đều”.

a/ Giả sử rằng, thoạt đầu ta trộn hai chất có nhiệt độ thấp hơn với nhau ta thu được một hỗn hợp ở nhiệt độ t < t3 ta có pt cân bằng nhiệt:
m1C1(t1 - t) = m2C2(t - t2)
\(t=\frac{m_1c_1t_1+m_2c_2t_2}{m_1c_1+m_2c_2}\left(1\right)\) (1)
Sau đó ta đem hỗn hgợp trên trôn với chất thứ 3 ta thu được hỗn hợp 3 chất ở nhiệt độ t' (t < t' < t3) ta có phương trình cân bằng nhiệt:
(m1C1 + m2C2)(t' - t) = m3C3(t3 - t') (2)
Từ (1) và (2) ta có:
\(t'=\frac{m_1c_1t_1+m_2c_2t_2+m_3c_3t_3}{m_1c_1+m_2c_2+m_3c_3}\)
Thay số vào ta tính được t' ≈ -190C
b/ Nhiệt lượng cần thiết để nâng nhiệt độ của hỗn hợp lên 60C:
Q = (m1C1 + m2C2 + m3C3) (t4 - t') = 1300000(J)


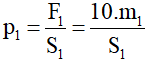
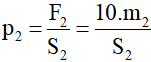
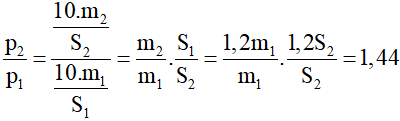
Câu trả lời:
a) Khi hai gương phẳng đặt vuông góc với nhau (90∘), một điểm sáng S giữa hai gương sẽ tạo ra 3 ảnh. Đây là do:
Vậy tổng cộng có 3 ảnh được tạo ra.
b) Khi hai gương phẳng G1 và G2 đặt song song, tia sáng tới SI phản xạ lần lượt trên G1 và G2. Để tính góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên G2, ta sử dụng các nguyên tắc quang học:
Do đó, tổng góc giữa tia tới SI ban đầu và tia phản xạ cuối cùng được tính dựa trên hình học của các gương.