Đổi 120 000 l = 120 m³ 

Chiều cao của hồ nước cũng chính là độ sâu của hồ và bằng:

120 : ( 8 \(\times\) 3) = 5 (m)

Kết luận chiều sâu của hồ nước là 5m 

Đổi \(120000l=120m^3\)

Ta có : \(V=d.r.h\Rightarrow h=\dfrac{V}{d.r}=\dfrac{120}{8.3}=\dfrac{120}{24}=5\left(m\right)\)

Vậy độ sâu của hồ nước là 5m.

Số học sinh trung bình bằng: 1 - \(\dfrac{1}{3}\) - \(\dfrac{2}{7}\) = \(\dfrac{8}{21}\)(số học sinh cả lớp)

16 học sinh ứng với: \(\dfrac{1}{3}\) - \(\dfrac{8}{21}\) = - \(\dfrac{1}{21}\) (xem lại đề bài đi em)

em cũng không biết nữa vì thấy đề giáo viên ra như vậy ạ

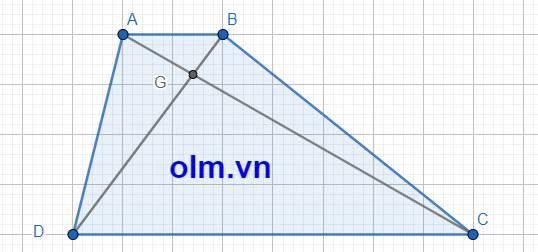
S_ABD  = S_{ABC (}vì hai tam giác có hai chiều cao bằng nhau và chung đáy AB)

⇒ S_ABG + S_ADG = S_ABG + S_BCG ⇒ S_ADG = S_BCG = 179,2 cm²

Vì \(\Delta\)ABG và \(\Delta\)BCG có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích \(\Delta\)ABG và \(\Delta\)BGC là tỉ số hai cạnh đáy:

\(\dfrac{AG}{GC}\) = \(\dfrac{44,8}{179,2}\) = \(\dfrac{1}{4}\)

Vì \(\Delta\)ADG và \(\Delta\)DCG có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích \(\Delta\)ADG và \(\Delta\)DCG là tỉ số hai cạnh đáy:

\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)

⇒S_DCG = S_ADG : \(\dfrac{1}{4}\) = 179,2 : \(\dfrac{1}{4}\) = 716,8 (cm²)

Diện tích của hình thang ABCD là:

44,8 + 179,2 + 179,2 + 716,8 = 1120 (cm²)

Đáp số: 1120 cm²

\(a,\) Chiều rộng chiếc bàn là :

\(\dfrac{5}{4}-\dfrac{1}{2}=\dfrac{3}{4}\left(m\right)\)

Chu vi chiếc bàn là :

\(\left(\dfrac{3}{4}+\dfrac{5}{4}\right)\times2=4\left(m\right)\)

\(b,\) Diện tích chiếc bàn là :

\(\dfrac{3}{4}\times\dfrac{5}{4}=\dfrac{15}{16}\left(m^2\right)\)

Số kg sơn dùng để sơn mặt bàn là :

\(\dfrac{15}{16}\times\dfrac{1}{3}=\dfrac{5}{16}\left(kg\right)\)

Đáp số : \(a,4m\)

               \(b,\dfrac{5}{16}kg\)

\(x+\dfrac{5}{2}=-\dfrac{1}{7}\)

\(\Rightarrow x=-\dfrac{1}{7}-\dfrac{5}{2}\)

\(\Rightarrow x=-\dfrac{2}{14}-\dfrac{35}{14}\)

\(\Rightarrow x=\dfrac{-2-35}{14}\)

\(\Rightarrow x=\dfrac{-37}{14}\)

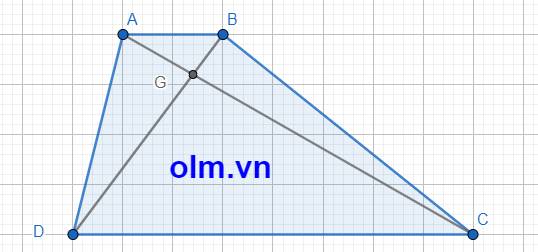
S_ABD = S_ABC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy AB)

⇒ S_ABG + S_ADG = S_ABG + S_BCG ⇒ S_ADG = S_BGC = 170,8 cm²

\(\Delta\)ABG và \(\Delta\)BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:

\(\dfrac{AG}{GC}\) = \(\dfrac{42,7}{170,8}\) = \(\dfrac{1}{4}\)

\(\Delta\)AGD và \(\Delta\)DGC có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và băng

\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)

⇒S_DGC = S_{AGD : \(\dfrac{1}{4}\)}

Diện tích tam giác DGC là: 170,8 : \(\dfrac{1}{4}\) = 683,2 (cm²)

Diện tích hình thang ABCD là:

42,7 + 170,8 + 170,8 + 683,2  = 1067,5 (cm²)

Đáp số: 1067,5 cm²

Tổng số học sinh của lớp 5D luôn luôn không đổi

a, Số học sinh trung bình bằng: 1 - \(\dfrac{1}{3}\) - \(\dfrac{2}{7}\) = \(\dfrac{8}{21}\)(số học sinh lớp 5D)

16 em ứng với phân số là: \(\dfrac{1}{3}\) - \(\dfrac{8}{21}\) = -\(\dfrac{1}{21}\)(số học sinh lớp 5D)

Xem lại đề bài em nhé

\(A=\left\{0;1;2;3;4;5\right\}\)

\(B=\) { \(x\in N|x\le5\) } 

Liệt kê phần tử tập B : \(B=\left\{0;1;2;3;4;5\right\}\)

\(\Rightarrow A=B\)

Vậy A là tập con của B hay B là tập con của A.

\(A=\left\{0;1;2;3;4;5\right\}\\ B=\left\{x\in N;5\le5\right\}\\ \Rightarrow B=\left\{0;2;3;4;5\right\}\)

Vậy \(A\subset B\) ; \(A\supset B\)

Đổi 200 kg = 2 tạ

Tổng số gạo cửa hàng bán được trong hai tuần là: 14 \(\times\)2 = 28 (tạ)

Ta có sơ đồ: 

Theo sơ đồ ta có:

Số gạo bán được trong tuần thứ nhất là:

(28 -2):2 = 13 (tạ)

Số gạo bán được trong tuần thứ hai là:

28 - 13 = 15 (tạ)

Đáp số: tuần thứ nhất bán 13 tạ gạo

             tuần thứ hai bán 15 tạ gạo 

A              =       1 + 2 + 2² + 2³  + ...+ 2¹⁰⁰

A\(\times\)2         =             2  + 2² + 2³ +...+ 2¹⁰⁰ + 2¹⁰¹

A \(\times\)2 - A   =      2¹⁰¹ - 1

A              =       2¹⁰¹ - 1