cho A bằng 1/9+1/16+1/25+...+1/6400.so sánh A với 1/4sos
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A<1/2-1/3 + 1/3-1/4 + 1/4 - 1/5 + .... +1/2024-1/2025
A<1/2 => 0<S<1
=> S Ko thuộc N
Công thức Tổng quát : 1/(n+1)^2 < 1/n+1/n+1
A<1/2-1/3 + 1/3-1/4 + 1/4 - 1/5 + .... +1/2024-1/2025
A<1/2 => 0<S<1
=> A Ko thuộc N
Công thức Tổng quát : 1/(n+1)^2 < 1/n+1/n+1
phần bên dưới tớ ghi nhầm hjhj

\(\dfrac{2^2}{1\cdot3}\cdot\dfrac{3^2}{2\cdot4}\cdot...\cdot\dfrac{59^2}{58\cdot60}\)
\(=\dfrac{2\cdot3\cdot...\cdot59}{1\cdot2\cdot...\cdot58}\cdot\dfrac{2\cdot3\cdot...\cdot59}{3\cdot4\cdot...\cdot60}\)
\(=\dfrac{59}{1}\cdot\dfrac{2}{60}=\dfrac{59}{30}\)
=2.2/1.3 + 3.3/2.4 + 4.4/3.5 + ... + 59.59/58.60
=2.3.4. ... . 59 /1.2.3. ... . 58 + 2.3.4. ... .59 / 3.4.5. ... .60
=(RÚT GỌN ĐI) = 59/1 + 2/60
= 59+1/30
= 59 và 1/30


Gọi số bánh trong mỗi hộp là x(cái)
(Điều kiện: \(x\in Z^+\))
\(40=2^3\cdot5;28=2^2\cdot7\)
=>\(ƯCLN\left(40;28\right)=2^2=4\)
Vì số bánh trong mỗi hộp là như nhau
nên \(x\inƯC\left(40;28\right)\)
=>\(x\inƯ\left(4\right)\)
mà x>2
nên x=4(nhận)
Vậy: Mỗi hộp có 4 chiếc bánh

\(\left[\left(4-x\right)\cdot3+51\right]:3-2^2=14\)
=>\(\left(4-x+17\right)-4=14\)
=>21-4-x=14
=>17-x=14
=>x=3

Sau ngày thứ nhất số trang sách còn lại chiếm:
\(1-\dfrac{1}{3}=\dfrac{2}{3}\)(quyển sách)
Sau ngày thứ hai thì số trang sách còn lại chiếm:
\(\dfrac{2}{3}\left(1-\dfrac{5}{8}\right)=\dfrac{2}{3}\cdot\dfrac{3}{8}=\dfrac{1}{4}\)(tổng số trang)
Số trang sách của quyển sách đó là:
\(90:\dfrac{1}{4}=360\left(trang\right)\)

\(\dfrac{x-1}{12}+\dfrac{x-1}{20}+\dfrac{x-1}{30}+\dfrac{x-1}{42}+\dfrac{x-1}{56}+\dfrac{x-1}{72}=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{3}-\dfrac{1}{9}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\cdot\dfrac{2}{9}=\dfrac{16}{9}\)
=>x-1=8
=>x=9

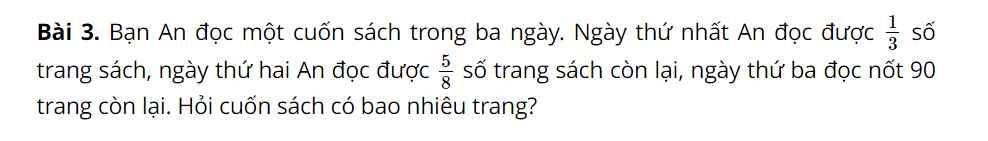
A=41+91+161+251+361
𝐴=122+132+142+152+162A=221+321+421+521+621
𝐴<11.2+12.3+13.4+14.5+15.6A<1.21+2.31+3.41+4.51+5.61
⇒𝐴<1−16⇒A<1−61
Mà 1−16=56⇒𝐴<561−61=65⇒A<65
A = \(\dfrac{1}{9}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{25}\) + ... + \(\dfrac{1}{6400}\)
A = \(\dfrac{1}{3.3}\) + \(\dfrac{1}{4.4}\) + \(\dfrac{1}{5.5}\) + ... + \(\dfrac{1}{80.80}\)
\(\dfrac{1}{3.3}\) = \(\dfrac{1}{9}\)
\(\dfrac{1}{4.4}>\dfrac{1}{4.5}=\dfrac{1}{4}-\dfrac{1}{5}\)
\(\dfrac{1}{5.5}>\dfrac{1}{5.6}=\dfrac{1}{5}-\dfrac{1}{6}\)
................................
\(\dfrac{1}{80.80}>\dfrac{1}{80.81}=\dfrac{1}{80}-\dfrac{1}{81}\)
Cộng vế với vế ta có:
A = \(\dfrac{1}{3.3}+\dfrac{1}{4.4}+\dfrac{1}{5.5}+...+\dfrac{1}{80.80}\) > \(\dfrac{1}{9}\) + \(\dfrac{1}{4}-\dfrac{1}{81}\)
A > \(\dfrac{1}{4}+\left(\dfrac{1}{9}-\dfrac{1}{81}\right)\)
Vì \(\dfrac{1}{9}\) > \(\dfrac{1}{81}\) ⇒ \(\dfrac{1}{9}\) - \(\dfrac{1}{81}\) > 0 ⇒\(\dfrac{1}{4}\) + (\(\dfrac{1}{9}\) - \(\dfrac{1}{81}\)) > \(\dfrac{1}{4}\)
Kết luận:
A = \(\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}+...+\dfrac{1}{6400}\) > \(\dfrac{1}{4}\)