có một hàng rào hình tròn bao quanh một bãi cỏ 1m2 và một con dê đói vào trong hàng rào dây thừng dài bao nhiêu để cho con dê ăn chính xác nửa bãi cỏ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Do K là trung điểm của BC (gt)
\(\Rightarrow BK=CK\)
Xét \(\Delta AKB\) và \(\Delta DKC\) có:
\(AK=DK\left(gt\right)\)
\(\widehat{AKB}=\widehat{DKC}\) (đối đỉnh)
\(BK=CK\left(cmt\right)\)
\(\Rightarrow\Delta AKB=\Delta DKC\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABK}=\widehat{DCK}\) (hai góc tương ứng)
Mà \(\widehat{ABK}\) và \(\widehat{DCK}\) là hai góc so le trong
\(\Rightarrow AB\) // \(CD\)
b) Do \(\Delta ABC\) vuông tại A (gt)
\(\Rightarrow AB\perp AC\)
Mà \(AB\) // \(CD\) (cmt)
\(\Rightarrow CD\perp AC\)
Do \(\Delta AKB=\Delta DKC\left(cmt\right)\)
\(\Rightarrow AB=CD\) (hai cạnh tương ứng)
Do H là trung điểm của AC (gt)
\(\Rightarrow AH=CH\)
Xét hai tam giác vuông: \(\Delta ABH\) và \(\Delta CDH\) có:
\(AB=CD\left(cmt\right)\)
\(AH=CH\left(cmt\right)\)
\(\Rightarrow\Delta ABH=\Delta CDH\) (hai cạnh góc vuông)
c) Sửa đề: Chứng minh \(\Delta HBD\) cân
Do \(\Delta ABH=\Delta CDH\left(cmt\right)\)
\(\Rightarrow HB=HD\) (hai cạnh tương ứng)
\(\Rightarrow\Delta HBD\) cân tại H


a) Do CD là tia phân giác của \(\widehat{ACB}\left(gt\right)\)
\(\Rightarrow\widehat{ACD}=\widehat{BCD}\)
\(\Rightarrow\widehat{ACD}=\widehat{ECD}\)
Xét hai tam giác vuông: \(\Delta ACD\) và \(\Delta ECD\) có:
\(CD\) là cạnh chung
\(\widehat{ACD}=\widehat{ECD}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta ECD\) (cạnh huyền - góc nhọn)
b) Em xem lại đề nhé!

Hiệu số phần bằng nhau là:
5 −1=46-1=5 ( phần )
Tuổi ông 5 năm trước là:
60:4×5=7560:5×6=72 ( tuổi )
Tuổi ông hiện nay là:
75+5=8072+2=74 ( tuổi )
Đáp số: 8074 tuổi


Giờ thứ hai cho rồi mà em, em xem lại đề nhé.


Các số tự nhiên thỏa mãn đề bài:
\(489;579;678\)
Vậy có 3 số thỏa mãn
Vì c là số lẻ, ta có thể biểu diễn nó dưới dạng c = 2k + 1, với k là một số nguyên dương.
Substitute giá trị của c vào phương trình a + b + c = 21 ta có:
a + b + 2k + 1 = 21
a + b = 20 - 2k
Vì a < b < 21 - a - b, ta có thể thay bằng biến x và sử dụng phương pháp bisection để tìm nghiệm của x bằng cách tìm giá trị k thích hợp. Đặt f(k) = a + x + 2k + 1 - 21.
Vì a và x là số lẻ nên a + x là số chẵn, khi đó f(k) cũng là số chẵn.
Ta có thể kiểm tra giá trị của f(k) để tìm giá trị của x. Lưu ý rằng k phải thỏa mãn điều kiện k ≤ (21 - 1)/2 = 10.
Như vậy, để tìm số lẻ có ba chữ số thoả mãn điều kiện a < b < c và a + b + c = 21, ta có thể thực hiện các bước sau:
- Thử từng giá trị của k từ 1 đến 10:
- Với mỗi k, tính giá trị của f(k) = a + x + 2k + 1 - 21
- Nếu f(k) = 0 và a, x là số lẻ thì đó là một bộ số thỏa mãn. Nếu f(k) ≠ 0 hoặc a, x không phải số lẻ thì tiếp tục thử k tiếp theo.
- Tổng hợp tất cả các bộ số thỏa mãn để có số lẻ có ba chữ số thoả mãn yêu cầu của bài toán.
Ví dụ, thử với k = 1, ta có:
a + x = 20 - 2(1) = 18
f(1) = a + x + 3 - 21 = a + x - 18
Nếu a + x là số lẻ, thì ta phải có a + x - 18 là số lẻ và bằng 1, 3, 5, 7 hoặc 9.
- Nếu a + x - 18 = 1, ta có a + x = 19, vậy có một bộ số là (9,9,3).
- Nếu a + x - 18 = 3, ta có a + x = 21, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.
- Nếu a + x - 18 = 5, ta có a + x = 23, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.
- Nếu a + x - 18 = 7, ta có a + x = 25, vậy có một bộ số là (7,11,3).
- Nếu a + x - 18 = 9, ta có a + x = 27, vậy không có bộ số nào là số lẻ và thoả mãn điều kiện.
Vậy có hai số lẻ có ba chữ số thoả mãn yêu cầu của bài toán, đó là 793 và 911.
Tick cho mình nha
\(\dfrac{178\times270+156}{179\times270-114}\)
\(=\dfrac{270\left(156+22\right)+156}{270\left(156+23\right)-114}\)
\(=\dfrac{270\times156+6096}{270\times156+6096}=1\)

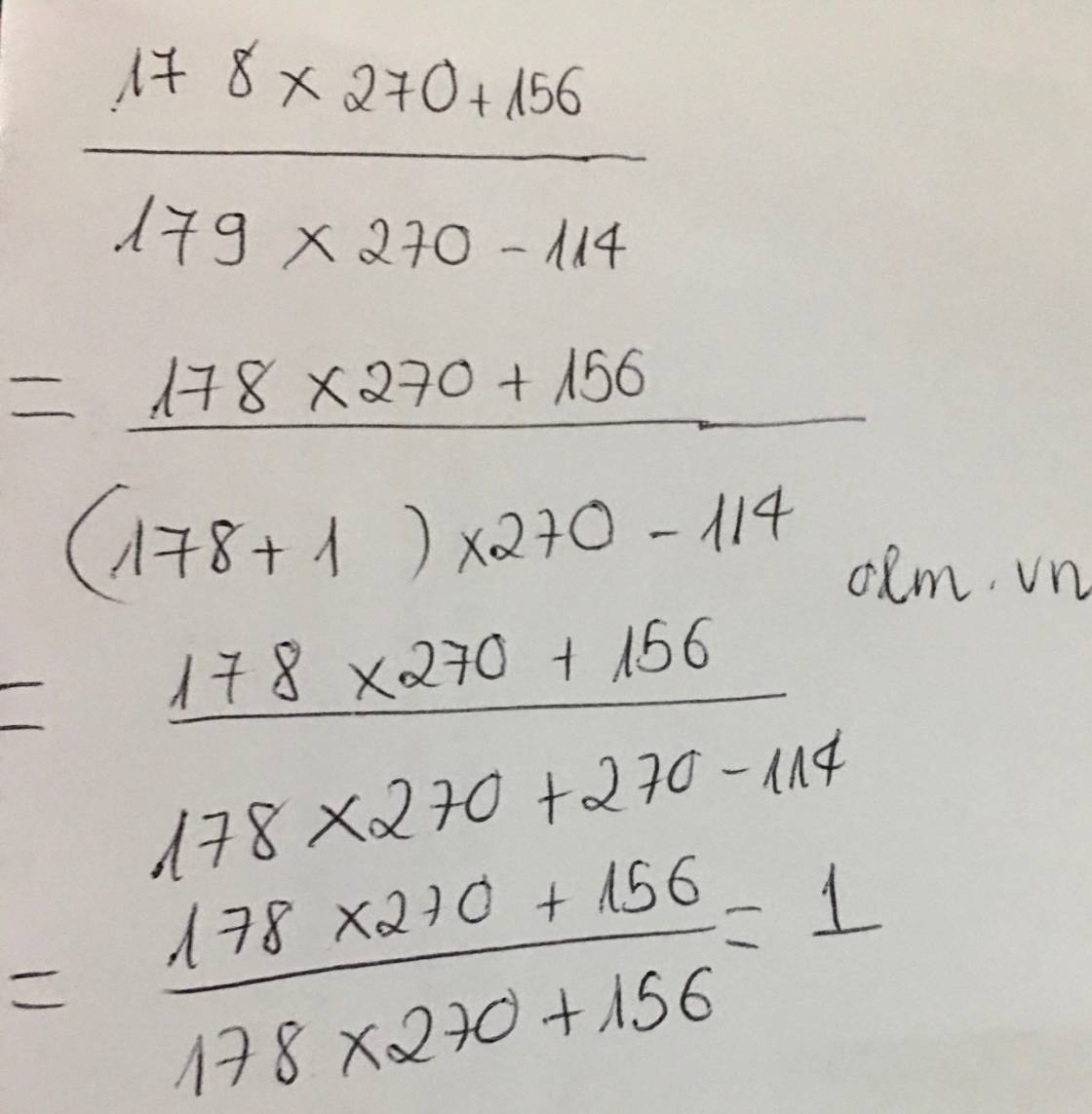
Thách lại bạn đó