Cho x+y=1. Tìm giá trị nhỏ nhất của P=x^2+y^2-1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(BC^2=AB^2+AC^2\) (Pitago)
\(\Rightarrow BC^2=6^2+8^2=100\Rightarrow BC=10cm\)
Theo định lý đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}\)
Mà \(BD+CD=BC=10cm\)
\(\Rightarrow CD=4x\frac{10}{3+4}=\frac{40}{7}cm\)
b/ Xét tg vuông DEC và tg vuông ABC có
\(\widehat{ACB}\) chung
\(\widehat{DEC}=\widehat{ABC}\) (cùng phụ với \(\widehat{ACB}\) )
=> tg DEC đồng dạng với tg ABC (g.g.g)
c/ ta có
\(\widehat{BAE}=90^o;\widehat{BDE}=90^o\) => A và D cùng nhìn BE dưới cùng 1 góc bằng 90 độ nên ABDE là tứ giác nội tiếp đường tròn
Ta có sđ\(\widehat{BAD}=\frac{1}{2}\) sđ cung BD \(=45^o\)(Góc nội tiếp)
sđ\(\widehat{BED}=\frac{1}{2}\) sđ cung BD (Góc nội tiếp)
\(\Rightarrow\widehat{BED}=\widehat{BAD}=45^o\)
Xét tg vuông BDE có
\(\widehat{EBD}=90^o-\widehat{BED}=90^o-45^o=45^o\)
\(\Rightarrow\widehat{EBD}=\widehat{BED}=45^o\) => tg BDE cân tại D


Gọi số tuổi của Nam hiện nay là x (tuổi) (điều kiện: \(x\inℕ^∗\)).
Hiện nay, số tuổi của bố Nam là: \(7x\)(tuổi).
5 năm sau, số tuổi của Nam là: \(x+5\)(tuổi).
5 năm sau, số tuổi của bố Nam là: \(7x+5\)(tuổi).
Vì 5 năm sau, tuổi bố gấp 4 lần tuổi Nam nên ta có phương trình:
\(4\left(x+5\right)=7x+5\).
\(\Leftrightarrow4x+20=7x+5\).
\(\Leftrightarrow4x-7x=5-20\).
\(\Leftrightarrow-3x=-15\).
\(\Leftrightarrow x=5\)(thỏa mãn điều kiện).
Vậy hiện nay, Nam 5 tuổi.

TH1 : Xét \(x< -2\)
\(\Leftrightarrow\left|x+2\right|+\left|7-x\right|=3x+4\)
\(\Leftrightarrow-x-2+7-x=3x+4\)
\(\Leftrightarrow-2x+5=3x+4\)
\(\Leftrightarrow x=\frac{1}{5}\)( loại )
TH2 : Xét \(-2< x< 7\)
\(\Leftrightarrow\left|x+2\right|+\left|7-x\right|=3x+4\)
\(\Leftrightarrow x+2+7-x=3x+4\)
\(\Leftrightarrow x=\frac{5}{3}\left(TM\right)\)
TH3 : Xét \(x\ge7\)
\(\Rightarrow x+2+7+x=3x+4\)
\(\Leftrightarrow x=-9\)( loại )
| \(x\) | \(-\infty\) \(-2\) \(7\) \(+\infty\) |
| \(x+2\) | \(-----\) \(0\) \(++++++++++\) |
| \(7-x\) | \(++++++++++\)\(0\)\(------\) |
Nếu \(x< -2\)
\(\rightarrow-\left(x+2\right)+\left(7-x\right)=3x+4\)
\(\Leftrightarrow-x-2+7-x-3x-4=0\)
\(\Leftrightarrow-5x=-1\)
\(\Leftrightarrow x=\frac{1}{5}\left(ktm\right)\)
Nếu \(-2\le x\le7\\ \rightarrow\left(x+2\right)+\left(7-x\right)=3x+4\)
\(\Leftrightarrow x+2+7-x=3x+4\)
\(\Leftrightarrow9-4=3x\\ \Leftrightarrow5=3x\)
\(\Leftrightarrow x=\frac{5}{3}\left(tm\right)\)
Nếu \(x>7\)
\(\rightarrow\left(x+2\right)-\left(7-x\right)=3x+4\)
\(\Leftrightarrow x+2-7+x=3x+4\)
\(\Leftrightarrow2x-5=3x+4\\ \Leftrightarrow x=-9\left(ktm\right)\)
Vậy, \(S=\left\{\frac{5}{3}\right\}\)
@Cừu
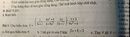
\(P=x^2+y^2-1\ge\frac{\left(x+y\right)^2}{2}-1\)
\(=\frac{1}{2}-1=-\frac{1}{2}\)
Vậy GTNN P là -1/2 khi x = 1/2
Áp dụng bất đẳng thức Bunyakovsky dạng phân thức ta có :
\(x^2+y^2=\frac{x^2}{1}+\frac{y^2}{1}\ge\frac{\left(x+y\right)^2}{1+1}=\frac{1^2}{2}=\frac{1}{2}\)
=> P = x2 + y2 - 1 ≥ 1/2 - 1 = -1/2
Dấu "=" xảy ra <=> x=y = 1/2 . Vậy MinP = -1/2