rút gọn phân thức (x+1)/(2-4x+2x^2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tuổi của người thứ hai cách đây 10 năm là x (x>0)
Tuổi của người thứ nhất cách đây 10 năm là: \(3x\)
Tuổi của người thứ nhất sau đây 2 năm là: \(3x+12\)
Tuổi của người thứ hai sau đây 2 năm là: \(x+12\)
Do sau đây 1 năm tuổi người thứu hai bằng 1 nửa tuổi người thứ nhất nên ta có pt:
\(x+12=\dfrac{1}{2}\left(3x+12\right)\)
\(\Leftrightarrow2x+24=3x+12\)
\(\Leftrightarrow x=12\)
Vậy tuổi của người thứ nhất hiện nay là \(3x+10=46\) tuổi, tuổi của người thứ hai hiện nay là \(x+10=22\) tuổi

6:
\(2x^2+3xy-2y^2=7\)
=>\(2x^2+4xy-xy-2y^2=7\)
=>\(2x\left(x+2y\right)-y\left(x+2y\right)=7\)
=>(x+2y)(2x-y)=7
=>\(\left(x+2y;2x-y\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)
TH1: \(\left\{{}\begin{matrix}x+2y=1\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5y=-5\\x+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)
=>Nhận
TH2: \(\left\{{}\begin{matrix}x+2y=7\\2x-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=7\\4x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=9\\2x-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1,8\\y=2x-1=2\cdot1,8-1=2,6\end{matrix}\right.\)
=>Loại
TH3: \(\left\{{}\begin{matrix}x+2y=-1\\2x-y=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=-2\\2x-y=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5y=-2+7=5\\2x-y=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\2x=-7+y=-7+1=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
=>Nhận
TH4: \(\left\{{}\begin{matrix}x+2y=-7\\2x-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=-7\\4x-2y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=-9\\2x-y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1,8\\y=2x+1=2\cdot\left(-1,8\right)+1=-2,6\end{matrix}\right.\)
=>Loại

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
ΔHBA~ΔABC
=>\(\dfrac{HA}{AC}=\dfrac{BA}{BC}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
c: Xét ΔDAB có DE là phân giác
nên \(\dfrac{EA}{EB}=\dfrac{DA}{DB}\)
Xét ΔDAC có DF là phân giác
nên \(\dfrac{FC}{FA}=\dfrac{DC}{DA}\)
\(\dfrac{EA}{EB}\cdot\dfrac{FC}{FA}\cdot\dfrac{DB}{DC}\)
\(=\dfrac{DA}{DB}\cdot\dfrac{DC}{DA}\cdot\dfrac{DB}{DC}=1\)

ĐKXĐ: \(x\notin\left\{0;3;1\right\}\)
\(\left(\dfrac{x+3}{x}-\dfrac{x}{x-3}+\dfrac{9}{x^2-3x}\right):\dfrac{2x-2}{x}\)
\(=\dfrac{\left(x+3\right)\left(x-3\right)-x^2+9}{x\left(x-3\right)}\cdot\dfrac{x}{2x-2}\)
\(=\dfrac{x^2-9-x^2+9}{x\left(x-3\right)}\cdot\dfrac{x}{2\left(x-1\right)}\)
=0

Xét ΔABF vuông tại F và ΔACE vuông tại E có
\(\widehat{BAF}\) chung
Do đó: ΔABF~ΔACE
=>\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Xét ΔAFE và ΔABC có
\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAFE~ΔABC

1:
a: Sửa đề: Chứng minh ΔAMB~ΔANC
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{MAB}=\widehat{NAC}\)
Do đó: ΔAMB~ΔANC
b: ΔAMB~ΔANC
=>\(\dfrac{AM}{AN}=\dfrac{MB}{NC}\)
Xét ΔDMB vuông tại M và ΔDNC vuông tại N có
\(\widehat{MDB}=\widehat{NDC}\)(hai góc đối đỉnh)
Do đó: ΔDMB~ΔDNC
=>\(\dfrac{DM}{DN}=\dfrac{BM}{NC}\)
=>\(\dfrac{DM}{DN}=\dfrac{AM}{AN}\)
=>\(DM\cdot AN=AM\cdot DN\)
1:
a: Sửa đề: Chứng minh ΔAMB~ΔANC
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{MAB}=\widehat{NAC}\)
Do đó: ΔAMB~ΔANC
b: ΔAMB~ΔANC
=>\(\dfrac{AM}{AN}=\dfrac{MB}{NC}\)
Xét ΔDMB vuông tại M và ΔDNC vuông tại N có
\(\widehat{MDB}=\widehat{NDC}\)(hai góc đối đỉnh)
Do đó: ΔDMB~ΔDNC
=>\(\dfrac{DM}{DN}=\dfrac{BM}{NC}\)
=>\(\dfrac{DM}{DN}=\dfrac{AM}{AN}\)
=>\(DM\cdot AN=AM\cdot DN\)

\(\dfrac{x}{2020}\) + \(\dfrac{x+1}{2021}\) + \(\dfrac{x+2}{2022}\) + \(\dfrac{x+3}{2023}\) = 4
\(\dfrac{x}{2020}\) + \(\dfrac{x+1}{2021}\) + \(\dfrac{x+2}{2022}\) + \(\dfrac{x+3}{2023}\) - 4 = 0
(\(\dfrac{x}{2020}\) - 1) + (\(\dfrac{x+1}{2021}\) - 1) + (\(\dfrac{x+2}{2022}\) - 1) + (\(\dfrac{x+3}{2023}\) - 1) = 0
\(\dfrac{x-2020}{2020}\) + \(\dfrac{x-2020}{2021}\) + \(\dfrac{x-2020}{2022}\) + \(\dfrac{x-2020}{2024}\) = 0
\(\left(x-2020\right)\).(\(\dfrac{1}{2020}\) + \(\dfrac{1}{2021}\) + \(\dfrac{1}{2022}\) + \(\dfrac{1}{2024}\)) = 0
\(x\) - 2020 = 0
\(x\) = 2020
Vậy \(x=2020\)

\(\dfrac{x+2}{98}\) + \(\dfrac{x+4}{96}\) = \(\dfrac{x+6}{94}\) + \(\dfrac{x+8}{92}\)
\(\dfrac{x+2}{98}\) + \(\dfrac{x+4}{96}\) - \(\dfrac{x+6}{94}\) - \(\dfrac{x+8}{92}\) = 0
\(\dfrac{x+2}{98}\) + 1 + \(\dfrac{x+4}{96}\) + 1 - ( \(\dfrac{x+6}{94}\) + 1) - (\(\dfrac{x+8}{92}\) + 1) = 0
\(\dfrac{x+2+98}{98}\) + \(\dfrac{x+4+96}{96}\) - \(\dfrac{x+6+94}{94}\) - \(\dfrac{x+2+98}{92}\) = 0
\(\dfrac{x+100}{98}\) + \(\dfrac{x+100}{96}\) - \(\dfrac{x+100}{94}\) - \(\dfrac{x+100}{92}\) = 0
(\(x\) + 100) \(\times\) (\(\dfrac{1}{98}\) + \(\dfrac{1}{96}\) - \(\dfrac{1}{94}\) - \(\dfrac{1}{92}\)) = 0
\(x\) - 100 = 0
\(x\) = - 100
Vậy \(x\) = - 100


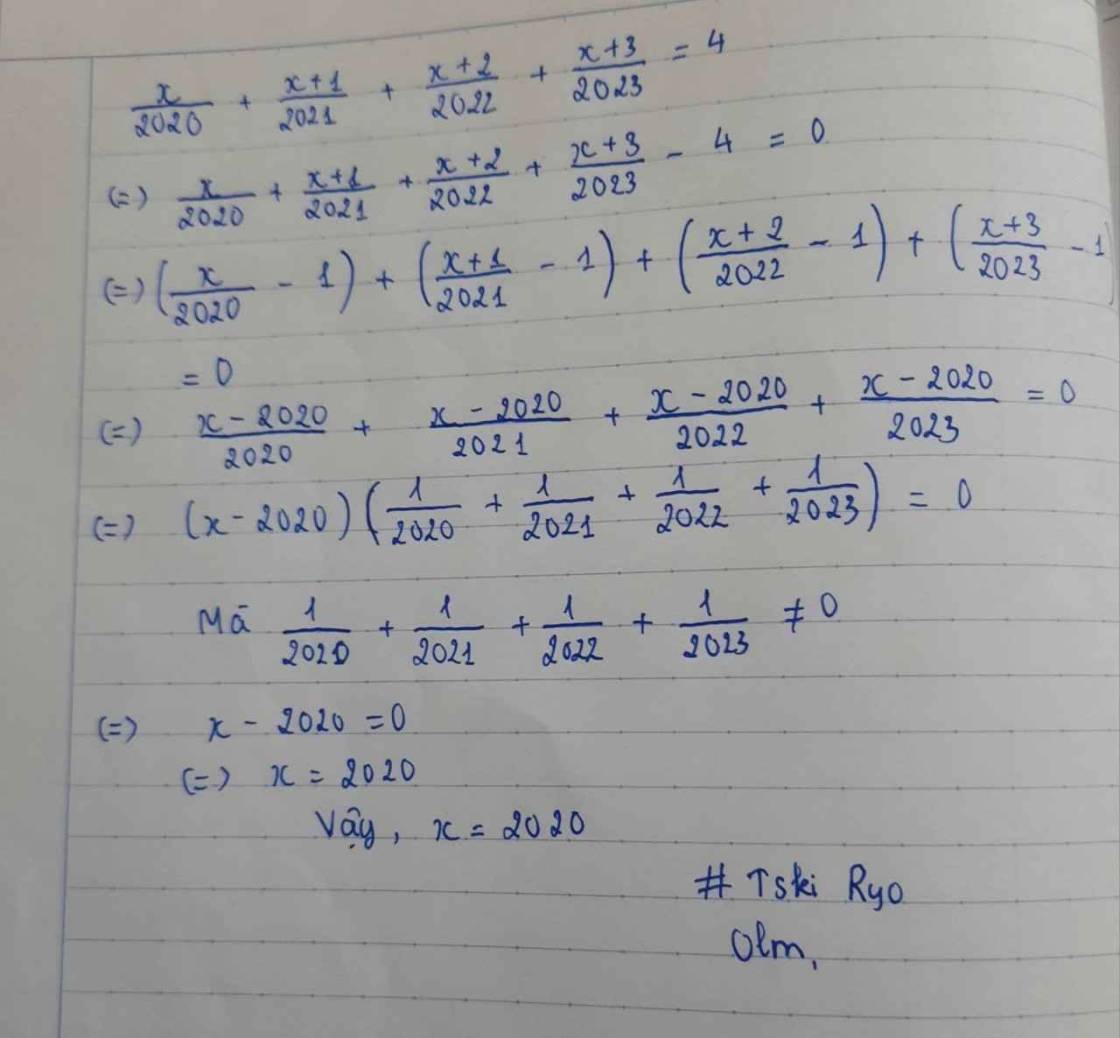
Phân thức này không rút gọn được nữa nha bạn