GIÚP TỚ VỚI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


E ơi đăng nhiều quá một lần khó nhận trợ giúp nha e, mình chia nhỏ bài ra nè

Bài 7:
a: \(5\cdot2^2+\left(x+3\right)=5^2\)
=>20+x+3=25
=>x+23=25
=>x=2
b: \(2^3+\left(x-3^2\right)=5^3-4^3\)
=>\(8+x-9=125-64=61\)
=>x=61+1=62
c:
\(4\left(x-5\right)-2^3=2^4\cdot3\)
=>\(4\left(x-5\right)=16\cdot3+8=8+48=56\)
=>x-5=14
=>x=19
d: \(5\left(x+7\right)-10=2^3\cdot5\)
=>5(x+7)-10=40
=>5(x+7)=50
=>x+7=10
=>x=3
Bài 3:
a: \(2^x+2^{x+3}=144\)
=>\(2^x+8\cdot2^x=144\)
=>\(9\cdot2^x=144\)
=>\(2^x=16\)
=>x=4
b: \(\left(x-5\right)^{2022}=\left(x-5\right)^{2021}\)
=>\(\left(x-5\right)^{2022}-\left(x-5\right)^{2021}=0\)
=>\(\left(x-5\right)^{2021}\left(x-5-1\right)=0\)
=>\(\left(x-5\right)^{2021}\cdot\left(x-6\right)=0\)
=>\(\left[{}\begin{matrix}x-5=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=6\end{matrix}\right.\)
c: \(\left(2x+1\right)^3=9\cdot81\)
=>\(\left(2x+1\right)^3=9^3\)
=>2x+1=9
=>2x=8
=>x=4

x(x+8)=20
=>\(x^2+8x-20=0\)
=>(x+10)(x-2)=0
=>\(\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
\(x\)(\(x+8\)) = 20
\(x^2\) + 8\(x\) = 20
\(x^2\) + 8\(x\) - 20 = 0
(\(x^2\) + 10\(x\)) - (2\(x\) + 10) = 0
\(x\)(\(x+10\)) - 2(\(x+10\)) = 0
(\(x+10\))(\(x-2\)) = 0
\(\left[{}\begin{matrix}x+10=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-10; 2}

\(4^2+5=y^2+y\\ =>16+5=y^2+y\\ =>21=y^2+y\\ =>y^2+y-21=0\\ =>\left(y^2+\dfrac{1}{2}y+\dfrac{1}{2}y+\dfrac{1}{4}\right)-\dfrac{85}{4}=0\\ =>\left[y\left(y+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(y+\dfrac{1}{2}\right)\right]=\dfrac{85}{4}\\ =>\left(y+\dfrac{1}{2}\right)\left(y+\dfrac{1}{2}\right)=\dfrac{85}{4}\\ =>\left(y+\dfrac{1}{2}\right)^2=\left(\dfrac{\sqrt{85}}{2}\right)^2\\ TH1:y+\dfrac{1}{2}=\dfrac{\sqrt{85}}{2}\\ =>y=\dfrac{\sqrt{85}-1}{2}\\ TH2:y+\dfrac{1}{2}=-\dfrac{\sqrt{85}}{2}\\ =>y=\dfrac{-\sqrt{85}-1}{2}\)

\(100-x:15=10,5\\ x:15=100-10,5\\ x:15=89,5\\ x=15\times89,5\\ x=1342,5\)
Vậy: ...
100 - x : 15 = 10,5
x : 15 = 100 - 10,5
x : 15 = 89,5
x = 89,5 × 15
x = 1342,5
~~~ the end~~~

\(\left(\dfrac{3}{4}\times x\right):\dfrac{1}{2}=\dfrac{4}{5}\\ \dfrac{3}{4}\times x=\dfrac{4}{5}\times\dfrac{1}{2}\\ \dfrac{3}{4}\times x=\dfrac{4\times1}{5\times2}\\ \dfrac{3}{4}\times x=\dfrac{2}{5}\\ x=\dfrac{2}{5}:\dfrac{3}{4}\\ x=\dfrac{2}{5}\times\dfrac{4}{3}\\ x=\dfrac{2\times4}{5\times3}\\ x=\dfrac{8}{15}\)
Vậy: ...

\(15\times8-\left(17-30+83\right)-144:6\\ =15\times8-\left[\left(17+83\right)-30\right]-24\\ =120-\left(100-30\right)-24\\ =120-70-24\\ =50-24\\ =26\)

\(a,7\cdot7\cdot7\cdot7\\ =7^1\cdot7^1\cdot7^1\cdot7^1\\ =7^{1+1+1+1}=7^4\\ b,7\cdot35\cdot7\cdot25\\ =7\cdot\left(5\cdot7\right)\cdot7\cdot\left(5^2\right)\\ =7\cdot5\cdot7\cdot7\cdot5^2\\ =\left(7\cdot7\cdot7\right)\cdot\left(5\cdot5^2\right)\\ =\left(7^1\cdot7^1\cdot7^1\right)\cdot\left(5^1\cdot5^2\right)\\ =7^{1+1+1}\cdot5^{1+2}\\ =7^3\cdot5^3\\ c,2\cdot3\cdot8\cdot12\cdot24\\ =2\cdot3\cdot2^3\cdot\left(2^2\cdot3\right)\cdot\left(2^3\cdot3\right)\\ =\left(2\cdot2^3\cdot2^2\cdot2^3\right)\cdot\left(3\cdot3\cdot3\right)\\ =\left(2^1\cdot2^3\cdot2^2\cdot2^3\right)\cdot\left(3^1\cdot3^1\cdot3^1\right)\\ =2^{1+3+2+3}\cdot3^{1+1+1}\\ =2^9\cdot3^3\\ d,x\cdot x\cdot y\cdot y\cdot x\cdot y\cdot x\\ =\left(x\cdot x\cdot x\cdot x\right)\cdot\left(y\cdot y\cdot y\right)\\ =\left(x^1\cdot x^1\cdot x^1\cdot x^1\right)\cdot\left(y^1\cdot y^1\cdot y^1\right)\\ =x^{1+1+1+1}\cdot y^{1+1+1}\\ =x^4\cdot y^3\)

\(\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{9}\right)=\dfrac{a}{75}\\ =>\dfrac{3}{4}\cdot\dfrac{4}{5}\cdot\dfrac{5}{6}\cdot\dfrac{6}{7}\cdot\dfrac{7}{8}\cdot\dfrac{8}{9}=\dfrac{a}{75}\\ =>\dfrac{3\cdot\left(4\cdot5\cdot6\cdot7\cdot8\right)}{\left(4\cdot5\cdot6\cdot7\cdot8\right)\cdot9}=\dfrac{a}{75}\\ =>\dfrac{3}{9}=\dfrac{a}{75}\\ =>\dfrac{a}{75}=\dfrac{1}{3}\\ =>a=\dfrac{1}{3}\cdot75\\ =>a=25\)
Vậy: ...


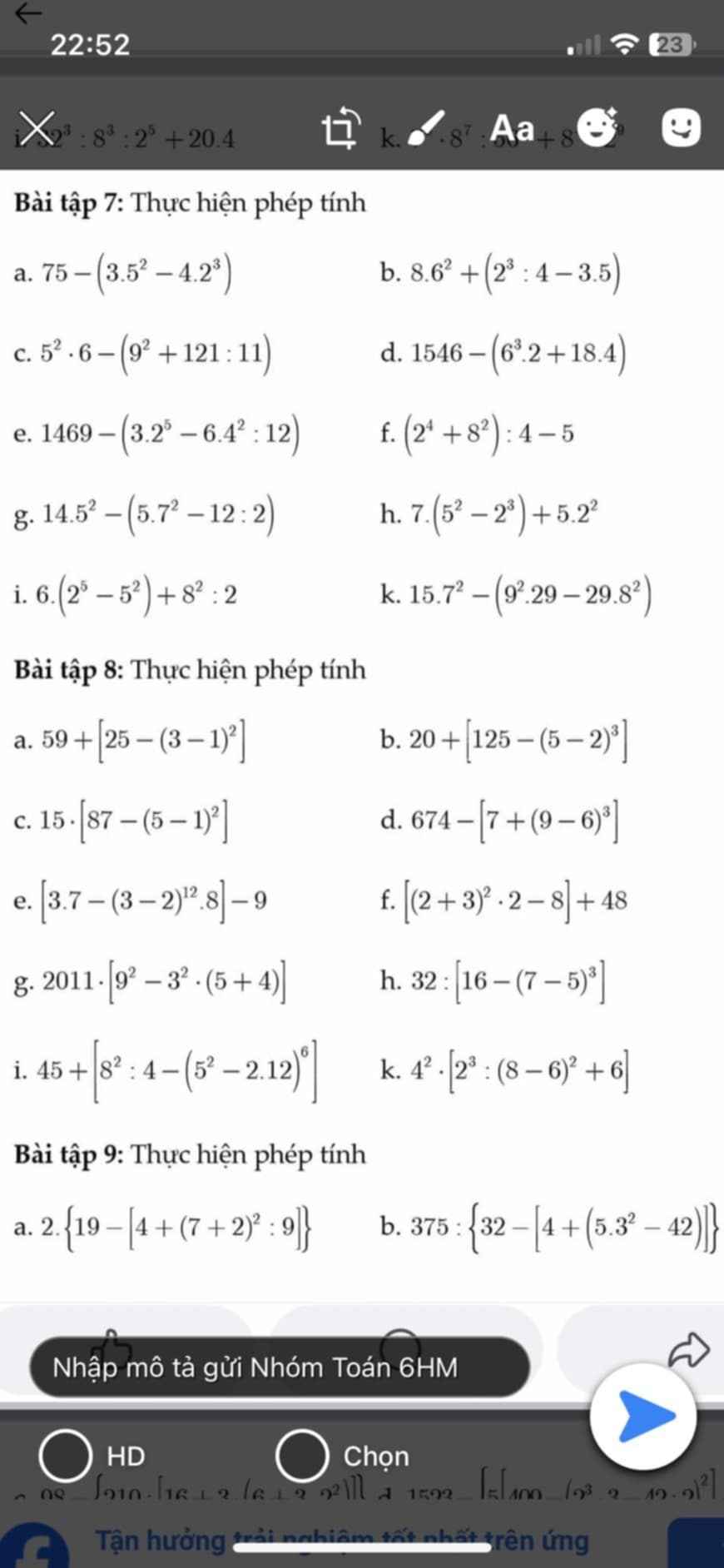

a: \(5\cdot5^2\cdot5^4\cdot5^8=5^{1+2+4+8}=5^{15}\)
b: \(2^3\cdot2^4\cdot2^5:2^6=2^{3+4+5-6}=2^6\)
c: \(x^2\cdot x^3:x^4\cdot x^7=x^{2+3-4+7}=x^8\)
d: \(\left(7^3:7^2\right)\cdot\left(7^2\cdot7^4\right):\left(7^2\cdot7\right)\)
\(=7\cdot7^6:7^3\)
\(=7^7:7^3=7^4\)
Cảm ơn