chỉ em bài này với 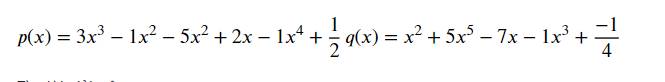 a) sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến
a) sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến
b) Tính P(x)+Q(x) và P(x)-Q(x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi các số đó là: \(x_1;x_2;...;x_{100}\)
Giả dụ các số đó có thứ tự từ nhỏ đến lớn: \(x_1< x_2< ...< x_{100}\)
Ta có: \(x_1.x_2.x_{100}< 0\)
\(\Rightarrow x_1\left(-\right);x_2;x_{100}\left(+\right)\) hoặc \(x_1;x_2;x_{100}\left(-\right)\)
Trường hợp 1: \(x_1\left(-\right);x_2;x_{100}\left(+\right)\)
Do \(x_2;x_{100}\left(+\right)\) mà \(x_2< ...< x_{100}\)
\(\Rightarrow x_2;...;x_{100}\) đều là số dương
\(\Rightarrow x_2.x_3.x_4>0\) (Mâu thuẫn với đề.)
Trường hợp 2: \(x_1;x_2;x_{100}\left(+\right)\)
Do \(x_2< ...< x_{100}\)
\(\Rightarrow x_1;...;x_{100}\) đều là số âm
Vậy tất cả 100 số đó đều là số âm.

Ta xét `: x^2 + 4x + 2 = 0`
`=> x^2 + 2x + 2x + 2 =0`
`=> x^2 + 2x + 2x + 4 =2`
`=> ( x + 2 )^2 = 2 =` \(\sqrt{2}^2\) `=` \(-\left(\sqrt{2}\right)^2\)
`=> x + 2 =` \(\sqrt{2}\) hoặc `x + 2=` \(-\sqrt{2}\)
`=> x =` \(\sqrt{2}-2\) hoặc `x =` \(-\sqrt{2}-2\)
Vậy `x in {` \(\sqrt{2}-2\) `;` \(-\sqrt{2}-2\) }` là nghiệm của `x^2 + 4x + 2`

Ta có `:`
`( 4n-6 )/( 3-2n ) = -( ( 4n-6 )/( 2n-3 )) = -2`
`=> ( 4n-6 )/( 3-2n )=-2 AAx`
`=>` Đề sai `bb!`

Gọi số cà chua bác Năm có là 100%.
Theo đề cho, có:
Bác Năm bán 60% cà chua, còn lại 40% cà chua và loại bỏ 10% chỗ còn lại (do bị hỏng)
\(\rightarrow\)Bác Năm còn lại 30% cà chua
Số cà chua bán được vào ngày hôm sau chiếm \(\dfrac{2}{3}\) của 30%
Số cà chua bán được vào ngày hôm sau là:
\(30\%.\dfrac{2}{3}=\dfrac{1}{5}=20\%\)
Mà số cà chua còn lại là 30%
\(\rightarrow\)Số cà chua ngày hôm sau bị đổ đi là 10%
Số phầm trăm cà chia hỏng mà bác Năm đổ đi là:
\(10\%+10\%=20\%\)

ĐÁP ÁN EM LÀM LÀ 74 SỐ KHÓM HOA CẤN TRỒNG. sAO LẠI LÀ 70 KHÓM ĐƯỢC Ạ?
Dọc theo chiều dài, ta trồng được:
5.5:\dfrac{1}{4}=225.5:41=22 (khóm hoa)
Dọc theo chiều rộng, ta trồng được:
3,75:\dfrac{1}{4}=153,75:41=15 (khóm hoa)
Như vậy, số khóm hoa trồng được dọc theo hai cạnh của mảnh vườn là:
[(22+15).2 ] -4=70[(22+15).2]−4=70 (khóm hoa)

\(a,1\dfrac{1}{5}+\dfrac{4}{5}:x=0,75\\ \dfrac{ 4}{5}:x=\dfrac{3}{4}-\dfrac{6}{4}\\ \dfrac{4}{5}:x=-\dfrac{3}{4}\\ x=\dfrac{4}{5}:\left(-\dfrac{3}{4}\right)\\ x=-\dfrac{16}{15}\\ b,x+\dfrac{1}{2}=1-x\\ x+x=1-\dfrac{1}{2}\\ 2x=\dfrac{1}{2}\\ x=\dfrac{1}{2}:2\\ x=\dfrac{1}{4}\)
$ \dfrac{1}{5}+\dfrac{4}{5}: x=0,75$;
b) $x+\dfrac{1}{2}=1-x$.
Em bị trục trặc và nhìn thấy phần câu hỏi bị thế này ạ. Em nhìn em không giải được ạ

\(a,\dfrac{2}{3}.\dfrac{5}{4}-\dfrac{3}{4}.\dfrac{2}{3}=\dfrac{2}{3}.\left(\dfrac{5}{4}-\dfrac{3}{4}\right)=\dfrac{2}{3}.\dfrac{2}{4}=\dfrac{1}{3}\)
\(b,2.\left(\dfrac{-3}{2}\right)-\dfrac{7}{2}=-6.\dfrac{1}{2}-7.\dfrac{1}{2}=\left(-6-7\right).\dfrac{1}{2}=-13.\dfrac{1}{2}=\dfrac{-13}{2}\)
\(c,-\dfrac{3}{4}.5\dfrac{3}{13}-0,75.\dfrac{36}{13}=-\dfrac{3}{4}.\left(\dfrac{68}{13}-\dfrac{36}{13}\right)=-\dfrac{3}{4}.\dfrac{32}{13}=-\dfrac{24}{13}\)
a) \(\dfrac{2}{3}.\dfrac{5}{4}-\dfrac{3}{4}.\dfrac{2}{3}\)
\(=\dfrac{2}{3}.\left(\dfrac{5}{4}-\dfrac{3}{4}\right)\)
\(=\dfrac{2}{3}.\dfrac{2}{4}\)
\(=\dfrac{2}{3}.\dfrac{1}{2}\)
\(=\dfrac{1}{3}\)
b) \(2.\left(\dfrac{-3}{2}\right)^2-\dfrac{7}{2}\)
\(=2.\dfrac{9}{4}-\dfrac{7}{2}\)
\(=\dfrac{9}{2}-\dfrac{7}{2}\)
\(=\dfrac{2}{2}=1\)
c) \(-\dfrac{3}{4}.5\dfrac{3}{13}-0,75.\dfrac{36}{13}\)
\(=-\dfrac{3}{4}.\dfrac{68}{13}-\dfrac{3}{4}.\dfrac{36}{13}\)
\(=\dfrac{3}{4}.\dfrac{-68}{13}-\dfrac{3}{4}.\dfrac{36}{13}\)
\(=\dfrac{3}{4}.\left(\dfrac{-68}{13}-\dfrac{36}{13}\right)\)
\(=\dfrac{3}{4}.\dfrac{-104}{13}\)
\(=\dfrac{3}{4}.\left(-8\right)\)
\(=-6\)

\(a\left(x\right)=10x-7\\ a\left(x\right)=0\Rightarrow10x-7=0\Rightarrow x=\dfrac{7}{10}\)
Vậy nghiệm của \(a\left(x\right)\) là \(x=\dfrac{7}{10}\)
\(b\left(x\right)=16x^2-x\\ b\left(x\right)=0\Rightarrow16x^2-x=0\Rightarrow x\left(16x-1\right)=0\)
TH1: \(x=0\)
TH2: \(16x-1=0\Rightarrow x=\dfrac{1}{16}\)
Vậy nghiệm của \(b\left(x\right)\) là \(x=0,x=\dfrac{1}{16}\)

(Tự vẽ hình)
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta ABD\) và \(\Delta HBD\) có:
\(\widehat{BAD}=\widehat{BHD}=90^0\)
\(BD\) chung
\(\widehat{ABD}=\widehat{HBD}\) (tính chất phân giác)
\(\Rightarrow\Delta ABD=\Delta HBD\) (ch - gn)
c) Ta có \(\Delta ABD=\Delta HBD\Rightarrow AD=HD\)
Mà \(HD< DC\) (do \(\Delta HDC\) vuông tại \(H\))
\(\Rightarrow DA< DC\)
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AC^2+AB^2}=10cm\)
b, Xét tam giác BAD và tam giác BHD có
BD _ chung ; ^ABD = ^HBD ; ^BAD = ^BHD = 900
Vậy tam giác BAD = tam giác BHD ( ch-gn)
a, \(P\left(x\right)=-x^4+3x^3-6x^2+2x+\dfrac{1}{2}\)
\(Q\left(x\right)=5x^5-x^3+x^2-7x-\dfrac{1}{4}\)
b, Ta có \(P\left(x\right)+Q\left(x\right)=5x^5-x^4+2x^3-5x^2-5x+\dfrac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=-x^4+4x^3-7x^2+9x+\dfrac{3}{4}-5x^5\)