Cho a, b, c>0 thỏa mãn a+b+c=3. Chứng minh rằng; \(\sqrt{\frac{a+b}{2ab}}+\sqrt{\frac{b+c}{2bc}}+\sqrt{\frac{c+a}{2ca}}\ge3.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(a+11⋮a+3\)
\(a+3+8⋮a+3\)
\(8⋮a+3\)hay \(a+3\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
| a + 3 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| a | -2 | -4 | -1 | -5 | 1 | -7 | 5 | -11 |
b, \(a-3⋮a-14\)
\(a-14+11⋮a-14\)
\(11⋮a-14\)hay \(a-14\inƯ\left(11\right)\left\{\pm1;\pm11\right\}\)
| a - 14 | 1 | -1 | 11 | -11 |
| a | 13 | 13 | 25 | 3 |

a, \(\frac{x-2}{x+1}=\frac{x-3}{x+2}ĐK:x\ne-1;-2\)
\(\Leftrightarrow x^2-4=\left(x-3\right)\left(x+1\right)\Leftrightarrow x^2-4=x^2+x-3x-3\)
\(\Leftrightarrow2x-1=0\Leftrightarrow x=\frac{1}{2}\)
b, \(\frac{2x+1}{x-3}=\frac{2x-3}{x+1}ĐK:x\ne3;-1\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)=\left(2x-3\right)\left(x-3\right)\)
\(\Leftrightarrow2x^2+2x+x+1=2x^2-6x-3x+9\)
\(\Leftrightarrow2x^2+3x+1-2x^2+9x-9=0\)
\(\Leftrightarrow12x-8=0\Leftrightarrow x=\frac{2}{3}\)

Ta luôn có \(4\left(x^3+y^3\right)\ge\left(x+y\right)^3\)(*)
Thật vậy: (*)\(\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\)*Đúng với mọi x, y thực dương*
\(\Rightarrow\sqrt[3]{4\left(x^3+y^3\right)}\ge x+y\)
Tương tự, ta có: \(\sqrt[3]{4\left(y^3+z^3\right)}\ge y+z,\sqrt[3]{4\left(z^3+x^3\right)}\ge z+x\)
Cộng theo vế ba bất đẳng thức trên, ta được: \(\sqrt[3]{4\left(x^3+y^3\right)}+\sqrt[3]{4\left(y^3+z^3\right)}+\sqrt[3]{4\left(z^3+x^3\right)}\ge2\left(x+y+z\right)\)
Ta cần chứng minh \(\left(x+y+z\right)+\left(\frac{x}{y^2}+\frac{y}{z^2}+\frac{z}{x^2}\right)\ge6\)
Thật vậy, ta có: \(\left(x+y+z\right)+\left(\frac{x}{y^2}+\frac{y}{z^2}+\frac{z}{x^2}\right)\ge3\sqrt[3]{xyz}+\frac{3}{\sqrt[3]{xyz}}\ge3.2=6\)
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi x = y = z

ĐKXĐ : \(\hept{\begin{cases}x\ge0\\x\ne4\\x\ne9\end{cases}}\)
\(=\left(\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\right)\div\frac{1}{2\left(\sqrt{x}-2\right)}\)
\(=\left(\frac{x-4}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\frac{x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\right)\times\frac{2\left(\sqrt{x}-2\right)}{1}\)
\(=\left(\frac{x-4-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\right)\times\frac{2\left(\sqrt{x}-2\right)}{1}\)
\(=\frac{5}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\times\frac{2\left(\sqrt{x}-2\right)}{1}\)
\(=\frac{5\times2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\frac{10}{\sqrt{x}-3}\)
\(\left(\frac{\sqrt{x}+2}{\sqrt{x}-3}-\frac{\sqrt{x}+3}{\sqrt{x}-2}\right):\frac{1}{2\sqrt{x}-4}\)
\(=\left(\frac{x-4}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\frac{x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\right):\frac{1}{2\sqrt{x}-4}\)
\(=\frac{5}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}.\frac{2\left(\sqrt{x}-2\right)}{1}\)
\(=\frac{10\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\frac{10}{\sqrt{x}-3}\)

BĐT cần chứng minh tương đương với:
\(\frac{a}{b}-\frac{a}{b+c}+\frac{b}{c}-\frac{b}{c+a}+\frac{c}{a}-\frac{c}{a+b}\ge\frac{3}{2}\)
\(\Leftrightarrow\frac{ac}{b\left(b+c\right)}+\frac{ba}{c\left(c+a\right)}+\frac{cb}{a\left(a+b\right)}\ge\frac{3}{2}\)
Ta có:
\(\frac{ac}{b\left(b+c\right)}+\frac{ba}{c\left(c+a\right)}+\frac{cb}{a\left(a+b\right)}\)
\(=\frac{a^2c^2}{abc\left(b+c\right)}+\frac{b^2a^2}{abc\left(c+a\right)}+\frac{c^2b^2}{abc\left(a+b\right)}\)
\(\ge\frac{\left(ab+bc+ca\right)^2}{abc\left(a+b\right)+abc\left(b+c\right)+abc\left(c+a\right)}\)
\(=\frac{\left(ab+bc+ca\right)^2}{2abc\left(a+b+c\right)}\)
Bất đẳng thức cần chứng minh sẽ đúng nếu ta chứng minh được \(\frac{\left(ab+bc+ca\right)^2}{abc\left(a+b+c\right)}\ge3\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\)
Đặt \(ab=x,bc=y,ca=z\)suy ra ta cần chứng minh
\(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx\ge3xy+3yz+3zx\)
\(\Leftrightarrow x^2+y^2+z^2\ge xy+yz+zx\)(đúng)
Vậy bất đẳng thức ban đầu là đúng.
Dấu \(=\)xảy ra khi \(a=b=c\).

Xét tam giác AMC và tam giác ABM ta có :
AM chung
AC = AB
BM = MC ( vì M là trung điểm )
^AMC = ^AMB ( 2 góc tương ứng )
Vì ^AMB = ^AMC (cmt)
Mà ^AMB + ^AMC = 180^0 ( 2 góc kề bù )
=)) ^AMB = ^AMC = 90^0
Vậy AM \(\perp\)BC (đpcm)
Xét ΔΔAMB và ΔΔAMC có:
AM chung
AB = AC (gt)
MB = MC (suy từ gt)
=> ΔΔAMB = ΔΔAMC (c.c.c)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\) ( hai góc tương ứng )
mà \(\widehat{AMB}+\widehat{AMC}=180^o\) ( kề bù )
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
Do đó AM ⊥ BC.


\(\frac{x+y+z}{2}=\frac{x}{y+z-5}=\frac{y}{x+z+3}=\frac{z}{x+y+2}=\frac{x+y+z}{2\left(x+y+z\right)}=\frac{1}{2}\)
\(\Rightarrow\hept{\begin{cases}x+y+z=1\\2x=y+z-5\\2y=x+z+3\end{cases}\Leftrightarrow\hept{\begin{cases}x=-\frac{4}{3}\\y=\frac{4}{3}\\z=1\end{cases}}}\)
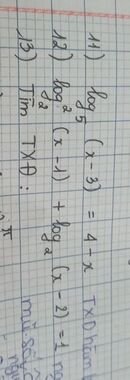
Áp dụng bđt: 2xy \(\le\)(x + y)2/2
khi đó, ta có: \(\sqrt{\frac{a+b}{2ab}}\ge\sqrt{\frac{a+b}{\frac{\left(a+b\right)^2}{2}}}=\sqrt{\frac{2}{a+b}}=\frac{1}{\sqrt{\frac{a+b}{2}}}\ge\frac{1}{\frac{\frac{a+b}{2}+1}{2}}=\frac{4}{a+b+2}\)
CMTT: \(\sqrt{\frac{b+c}{2bc}}\ge\frac{4}{b+c+2}\)
\(\sqrt{\frac{c+a}{2ca}}\ge\frac{4}{c+a+2}\)
=>Đặt A = \(\sqrt{\frac{a+b}{2ab}}+\sqrt{\frac{b+c}{2bc}}+\sqrt{\frac{a+c}{2ac}}\ge\frac{4}{a+b+2}+\frac{4}{b+c+2}+\frac{4}{a+c+2}\)
Áp dụng bđt svacso : \(\frac{x_1^2}{y_1}+\frac{x_2^2}{y_2}+\frac{x_3^2}{y_3}\ge\frac{\left(x_1+x_2+x_3\right)^2}{y_1+y_2+y_3}\)
ta có:
\(A\ge\frac{\left(2+2+2\right)^2}{a+b+2+b+c+2+a+c+2}=\frac{36}{2\left(a+b+c\right)+6}=\frac{36}{12}=3\)
=> Đpcm