Có hay không tam giác với độ dài các cạnh là 1,2dm ; 1dm và 2,4dm?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 4 2017
Gọi độ dài 3 cạnh của tam giác thứ tự là a,b,c (a > 0; b > 0; c > 0).
Vì độ dài 3 cạnh tỉ lệ với 3, 4, 9 nên:
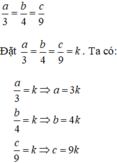
Suy ra: a + b = 3k + 4k = 7k < 9k (hay a + b < c)
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại)
Vậy không có tam giác nào có 3 cạnh tỉ lệ 3;4;9.
12 tháng 10 2017
Gọi độ dài 3 cạnh của tam giác thứ tự là a, b, c.
Theo đề bài ta có: a3=b4=c9a3=b4=c9
Đặt các tỉ số trên là k. Ta có:
a3=k⇒a=3ka3=k⇒a=3k
b4=k⇒b=4kb4=k⇒b=4k
c9=k⇒c=9kc9=k⇒c=9k
Suy ra: a + b = 3k + 4k = 7k < 9k
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại).
Vậy không có tam giác nào có 3 cạnh tỉ lệ với 3; 4; 9.
VK
2
PT
1
NT
0
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \({\sin ^2}A + {\cos ^2}A = 1\)
\( \Rightarrow \sin A = \pm \sqrt {1 - {{\cos }^2}A} \)
Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)
Ta có:
\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)
Thế vào công thức tính diện tích tam giác ABC ta được:
\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)
Chú ý:
Nếu tiếp tục biến đổi công thức diện tích ta được
\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)
Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:
\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)
(công thức Heron)
SG
1
18 tháng 5 2022
a: Vì 1+2=3 nên không có tam giác với số đo ba cạnh như vậy
b: Vì 1,2+1<2,4 nên không có tam giác với số đo ba cạnh như vậy
Không có, vì 1,2 + 1 không lớn hơn 2,4.