giả sử \(a,b\in Z^+\) sao cho \(\left(a+b\right)^2+a+b⋮ab\) . Gọi d là 1 ước chung của a và b . CMR \(d< \left[\sqrt{a+b}\right]\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 8 2016
sửa đề lại bạn nhé =) \(\frac{a}{A}=\frac{b}{B}=\frac{c}{C}=\frac{d}{D}\)
đặt \(\frac{a}{A}=\frac{b}{B}=\frac{c}{C}=\frac{d}{D}=k\Rightarrow\hept{\begin{cases}a=kA\\b=kB\end{cases}va\hept{\begin{cases}c=kC\\d=kD\end{cases}}}\)
theo đề bài ta có \(\sqrt{aA}+\sqrt{bB}+\sqrt{cC}+\sqrt{dD}=\sqrt{kA^2}+\sqrt{kB^2}+\sqrt{kC^2}+\sqrt{kD^2}\)
=\(\sqrt{k}\left(A+B+C+D\right)\left(1\right)\)
ta lại có \(\sqrt{\left(a+b+c+d\right)\left(A+B+C+D\right)}=\sqrt{\left(kA+kB+kC+kD\right)\left(A+B+C+D\right)}\)
=\(\sqrt{k\left(A+B+C+D\right)\left(A+B+C+D\right)}=\sqrt{k\left(A+B+C+D\right)^2}=\sqrt{k}\left(A+B+C+D\right)\left(2\right)\)
(1),(2)=> \(\sqrt{aA}+\sqrt{bB}+\sqrt{cC}+\sqrt{dD}=\sqrt{\left(a+b+c+d\right)\left(A+B+C+D\right)}\)
2 tháng 10 2021
\(P=\left(\dfrac{3\sqrt{a}}{a+\sqrt{ab}+\sqrt{b}}-\dfrac{3a}{a\sqrt{a}-b\sqrt{b}}+\dfrac{1}{\sqrt{a}-\sqrt{b}}\right):\dfrac{\left(a-1\right)\left(\sqrt{a}-\sqrt{b}\right)}{2a+2\sqrt{ab}+2b}\left(đk:a\ne b,a\ge0,b\ge0\right)\)
\(=\dfrac{3a-3\sqrt{ab}-3a+a+\sqrt{ab}+b}{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+\sqrt{b}\right)}.\dfrac{2\left(a+\sqrt{ab}+b\right)}{\left(a-1\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{a-2\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}.\dfrac{2}{\left(a-1\right)\left(\sqrt{a}-\sqrt{b}\right)}=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2.2}{\left(\sqrt{a}-\sqrt{b}\right)^2\left(a-1\right)}=\dfrac{2}{a-1}\in Z\)
\(\Rightarrow a-1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
Do \(a\ge0\)
\(\Rightarrow a\in\left\{0;2;3\right\}\)
2 tháng 10 2021
Ta có: \(P=\left(\dfrac{3\sqrt{a}}{a+\sqrt{ab}+b}-\dfrac{3a}{a\sqrt{a}-b\sqrt{b}}+\dfrac{1}{\sqrt{a}-\sqrt{b}}\right):\left(\dfrac{\left(a-1\right)\left(\sqrt{a}-\sqrt{b}\right)}{2a+2\sqrt{ab}+2b}\right)\)
\(=\dfrac{3a-3\sqrt{ab}-3a+a+\sqrt{ab}+b}{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}\cdot\dfrac{2\left(a+\sqrt{ab}+b\right)}{\left(a-1\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}-\sqrt{b}\right)^2}\cdot\dfrac{2}{a-1}\)
\(=\dfrac{2}{a-1}\)
Để P là số nguyên thì \(a-1\in\left\{1;-1;2;-2\right\}\)
hay \(a\in\left\{2;0;3\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1 2022
1. Đề sai, ví dụ (a;b;c)=(1;2;2) hay (1;2;7) gì đó
2. Theo nguyên lý Dirichlet, trong 4 số a;b;c;d luôn có ít nhất 2 số đồng dư khi chia 3.
Không mất tính tổng quát, giả sử đó là a và b thì \(a-b⋮3\)
Ta có 2 TH sau:
- Trong 4 số có 2 chẵn 2 lẻ, giả sử a, b chẵn và c, d lẻ \(\Rightarrow a-b,c-d\) đều chẵn \(\Rightarrow\left(a-b\right)\left(c-d\right)⋮4\)
\(\Rightarrow\) Tích đã cho chia hết 12
- Trong 4 số có nhiều hơn 3 số cùng tính chẵn lẽ, khi đó cũng luôn có 2 hiệu chẵn (tương tự TH trên) \(\Rightarrowđpcm\)
3. Với \(n=1\) thỏa mãn
Với \(n>1\) ta có \(3^n\equiv\left(5-2\right)^n\equiv\left(-2\right)^n\left(mod5\right)\)
\(\Rightarrow n.2^n+3^n\equiv n.2^n+\left(-2\right)^n\left(mod5\right)\)
Mặt khác \(n.2^n+\left(-2\right)^n=2^n\left(n+\left(-1\right)^n\right)\)
Mà \(2^n⋮̸5\Rightarrow n+\left(-1\right)^n⋮5\)
TH1: \(n=2k\Rightarrow2k+1⋮5\Rightarrow2k+1=5\left(2m+1\right)\Rightarrow k=5m+2\)
\(\Rightarrow n=10m+4\)
TH2: \(n=2k+1\Rightarrow2k+1-1⋮5\Rightarrow2k⋮5\Rightarrow k=5t\Rightarrow n=10t+1\)
Vậy với \(\left[{}\begin{matrix}n=10k+4\\n=10k+1\end{matrix}\right.\) (\(k\in N\)) thì số đã cho chia hết cho 5
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
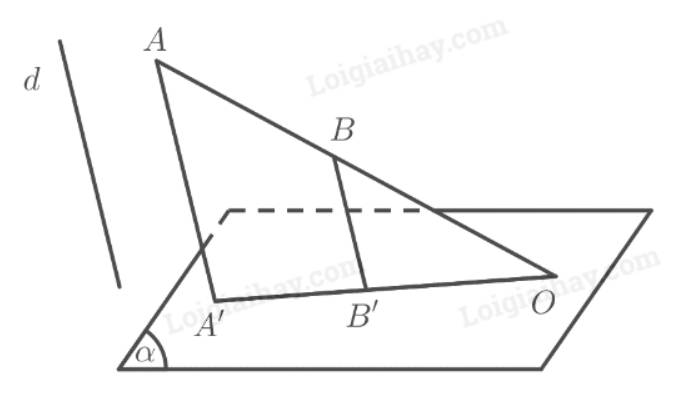
Vì \(O \in \left( \alpha \right)\) nên \(O\) là hình chiếu của chính nó lên mặt phẳng \(\left( \alpha \right)\) theo phương \(d\).
Vì ba điểm \(O,A,B\) thẳng hàng nên ba điểm \(O,A',B'\) thẳng hàng.
\(AA'\parallel BB' \Rightarrow \frac{{AB}}{{OA}} = \frac{{A'B'}}{{OA'}} \Leftrightarrow \frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}}\)
a) Để \(A'B' = AB\) thì \(OA' = OA\).
Vậy đường thẳng \(d\) song song với \(AA'\) và \(OA' = OA\).
b) Để \(A'B' = 2AB\) thì \(OA' = 2OA\).
Vậy đường thẳng \(d\) song song với \(AA'\) và \(OA' = 2OA\).
23 tháng 1 2019
1) Áp dụng BĐT bun-hi-a-cốp-xki ta có:
\(\left(a+d\right)\left(b+c\right)\ge\left(\sqrt{ab}+\sqrt{cd}\right)^2\)
\(\Leftrightarrow\sqrt{\left(a+d\right)\left(b+c\right)}\ge\sqrt{ab}+\sqrt{cd}\)( vì a,b,c,d dương )
Dấu " = " xảy ra \(\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
12 tháng 10 2018
Ta c/m bđt
với \(x,y,z\ge1\) thì: \(\frac{x+y}{1+z}+\frac{y+z}{1+x}+\frac{z+x}{1+y}\ge\frac{6\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}\) (*)
dấu bằng xảy ra khi x=y=z
bđt (*) \(\Leftrightarrow\left(\frac{x+y}{1+z}+1\right)+\left(\frac{y+z}{1+x}+1\right)+\left(\frac{z+x}{1+y}+1\right)\ge\frac{6\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}+3\)
\(\Leftrightarrow\left(x+y+z+1\right)\left(\frac{1}{1+z}+\frac{1}{1+x}+\frac{1}{1+y}\right)\ge\frac{3+9\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}\)
Ta có: \(1+x+y+z\ge1+3\sqrt[3]{xyz}\)(1)
Với \(x,y\ge1\) ta chứng minh \(\frac{1}{1+x}+\frac{1}{1+y}\ge\frac{2}{1+\sqrt{xy}}\)(2)
\(\Leftrightarrow\frac{2+\left(x+y\right)}{1+\left(x+y\right)+xy}\ge\frac{2}{1+\sqrt{xy}}\Leftrightarrow2+\left(x+y\right)+2\sqrt{xy}+\sqrt{xy}\left(x+y\right)\ge2+2\left(x+y\right)+2xy\)
\(\Leftrightarrow2\sqrt{xy}\left(1-\sqrt{xy}\right)+\left(x+y\right)\left(\sqrt{xy}-1\right)\ge0\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{xy}-1\right)\ge0\)
bđt trên luôn đúng =>DPCM
đợi mình làm vế sau nữa nhé tại máy lag nên làm đk đến đây thôi xíu nữa hoặc mai mik làm vế sau cho nhé
12 tháng 10 2018
Với \(x,y,z\ge1\) ta chứng minh: \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{1+\sqrt[3]{xyz}}\) (3)
\(\Leftrightarrow P=\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}+\frac{1}{1+\sqrt[3]{xyz}}\ge\frac{4}{1+\sqrt[3]{xyz}}\)
Áp dụng kết quả (2) ta thu được:
\(P\ge\frac{2}{1+\sqrt{xy}}+\frac{2}{1+\sqrt{z\sqrt[3]{xyz}}}\ge\frac{4}{1+\sqrt[4]{xyz\sqrt[3]{xyz}}}=\frac{4}{1+\sqrt[3]{xyz}}\)
Từ (1) và (3) suy ra (*) đúng
Trở lại bài toán: ta được bđt đã cho tưởng đương với:
\(\frac{\frac{1}{b}+\frac{1}{c}}{1+\frac{1}{a}}+\frac{\frac{1}{c}+\frac{1}{a}}{1+\frac{1}{b}}+\frac{\frac{1}{a}+\frac{1}{b}}{1+\frac{1}{c}}\ge\frac{\frac{6}{\sqrt[3]{abc}}}{1+\frac{1}{\sqrt[3]{abc}}}\)
Do x,y,z\(\le1\Rightarrow\frac{1}{x},\frac{1}{y},\frac{1}{z}\ge1\). Áp dụng (*) suy ra điều phải chứng minh dấu bằng xảy ra khi a=b=c