Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:Đặt $A=f(1)=a+b+c; B=f(-1)=a-b+c; C=f(0)=c$
Theo đề bài: $|A|, |B|, |C|\leq 1$
\(|a|+|b|+|c|=|\frac{A+B}{2}-C|+|\frac{A-B}{2}|+|C|\)
\(\leq |\frac{A+B}{2}|+|-C|+|\frac{A-B}{2}|+|C|=|\frac{A}{2}|+|\frac{B}{2}|+|C|+|\frac{A}{2}|+|\frac{-B}{2}|+|C|\)
\(=|A|+|B|+2|C|\leq 1+1+2=4\) (đpcm)

Dễ dàng c/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\)
Ta có : \(\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le\dfrac{1}{a+b+4}\le\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}\right)\)
Suy ra : \(\Sigma\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le2.\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}\right)=\dfrac{1}{2}.1=\dfrac{1}{2}\)
" = " \(\Leftrightarrow a=b=c=1\)

Bài 1
\(M=\dfrac{2x+y+z-15}{x}+\dfrac{x+2y+z-15}{y}+\dfrac{x+y+2z-15}{z}\)
\(M=\dfrac{x+12-15}{x}+\dfrac{y+12-15}{y}+\dfrac{z+12-15}{z}\)
\(M=\dfrac{x-3}{x}+\dfrac{y-3}{y}+\dfrac{z-3}{z}\)
\(M=1-\dfrac{3}{x}+1-\dfrac{3}{y}+1-\dfrac{3}{z}\)
\(M=3-\left(\dfrac{3}{x}+\dfrac{3}{y}+\dfrac{3}{z}\right)\)
\(M=3-3\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{\left(1+1+1\right)^2}{x+y+z}=\dfrac{9}{x+y+z}=\dfrac{3}{4}\)
\(\Rightarrow3\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\ge\dfrac{9}{4}\)
\(\Rightarrow3-3\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\le\dfrac{3}{4}\)
\(\Leftrightarrow M\le\dfrac{3}{4}\)
Vậy \(M_{max}=\dfrac{3}{4}\)
Dấu " = " xảy ra khi \(x=y=z=4\)
Bài 2
\(P=\dfrac{\left(a+b+c\right)^2}{30\left(a^2+b^2+c^2\right)}+\dfrac{a^3+b^3+c^3}{4abc}-\dfrac{131\left(a^2+b^2+c^2\right)}{60\left(ab+bc+ca\right)}\)
Xét \(\dfrac{a^3+b^3+c^3}{4abc}\)
\(=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc}{4abc}\)
\(=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)}{4abc}+\dfrac{3}{4}\)
\(=\dfrac{1}{4}\left(\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{ab}\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+\dfrac{3}{4}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge\dfrac{\left(1+1+1\right)^2}{ab+bc+ca}=\dfrac{9}{ab+bc+ca}\)
\(\Rightarrow\dfrac{1}{4}\left(\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{ab}\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+\dfrac{3}{4}\ge\dfrac{9\left(a^2+b^2+c^2-ab-bc-ca\right)}{4\left(ab+bc+ca\right)}+\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{4}\left(\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{ab}\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+\dfrac{3}{4}\ge\dfrac{9\left(a^2+b^2+c^2\right)-9\left(ab+bc+ca\right)}{4\left(ab+bc+ca\right)}+\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{4}\left(\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{ab}\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+\dfrac{3}{4}\ge\dfrac{9\left(a^2+b^2+c^2\right)}{4\left(ab+bc+ca\right)}-\dfrac{9}{4}+\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{4}\left(\dfrac{1}{bc}+\dfrac{1}{ca}+\dfrac{1}{ab}\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+\dfrac{3}{4}\ge\dfrac{9\left(a^2+b^2+c^2\right)}{4\left(ab+bc+ca\right)}-\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{a^3+b^3+c^3}{4abc}\ge\dfrac{9\left(a^2+b^2+c^2\right)}{4\left(ab+bc+ca\right)}-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{a^3+b^3+c^3}{4abc}-\dfrac{131\left(a^2+b^2+c^2\right)}{60\left(ab+bc+ca\right)}\ge\dfrac{9\left(a^2+b^2+c^2\right)}{4\left(ab+bc+ca\right)}-\dfrac{131\left(a^2+b^2+c^2\right)}{60\left(ab+bc+ca\right)}-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{a^3+b^3+c^3}{4abc}-\dfrac{131\left(a^2+b^2+c^2\right)}{60\left(ab+bc+ca\right)}\ge\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}-\dfrac{3}{2}\) (1)
Xét \(\dfrac{\left(a+b+c\right)^2}{30\left(a^2+b^2+c^2\right)}\)
\(=\dfrac{a^2+b^2+c^2+2\left(ab+bc+ca\right)}{30\left(a^2+b^2+c^2\right)}\)
\(=\dfrac{1}{30}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}\) (2)
Cộng (1) và (2) theo từng vế
\(P\ge\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}-\dfrac{22}{15}\)
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}\ge2\sqrt{\dfrac{\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)}{225\left(ab+bc+ca\right)\left(a^2+b^2+c^2\right)}}\)
\(\Rightarrow\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}\ge2\sqrt{\dfrac{1}{225}}\)
\(\Rightarrow\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}\ge\dfrac{2}{15}\)
\(P\ge\dfrac{a^2+b^2+c^2}{15\left(ab+bc+ca\right)}+\dfrac{ab+bc+ca}{15\left(a^2+b^2+c^2\right)}-\dfrac{22}{15}\ge\dfrac{2}{15}-\dfrac{22}{15}=-\dfrac{4}{3}\)
\(\Leftrightarrow P\ge-\dfrac{4}{3}\)
Vậy \(P_{min}=\dfrac{-4}{3}\)
Dấu " = " xảy ra khi \(a=b=c=1\)
Bài 1
\(M=\dfrac{2x+y+z-15}{x}+\dfrac{x+2y+z-15}{y}+\dfrac{x+y+2z-15}{z}\)

Lời giải:Vì $f(x)\geq 0$ nên $\Delta=b^2-4ac\leq 0$
$\Leftrightarrow 4ac\geq b^2$
Áp dụng BĐT AM-GM:
$Q=\frac{4a+c}{b}\geq \frac{4\sqrt{ac}}{b}\geq \frac{4\sqrt{b^2}}{b}=\frac{4b}{b}=4$
Vậy $Q_{\min}=4$

Bài 2: Restore : a;b;c không âm thỏa \(a^2+b^2+c^2=1\)
Tìm Min & Max của \(M=\left(a+b+c\right)^3+a\left(2bc-1\right)+b\left(2ac-1\right)+c\left(2ab-1\right)\)
Bài 4: Tương đương giống hôm nọ thôi : V
Bài 5 : Thiếu ĐK thì vứt luôn : V
Bài 7: Tương đương
( Hoặc có thể AM-GM khử căn , sau đó đổi \(\left(a;b;c\right)\rightarrow\left(\dfrac{x}{y};\dfrac{y}{z};\dfrac{z}{x}\right)\) rồi áp dụng bổ đề vasile)
Bài 8 : Đây là 1 dạng của BĐT hoán vị
@Ace Legona @Akai Haruma @Hung nguyen @Hà Nam Phan Đình @Neet
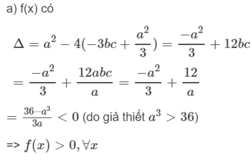
Lời giải
a) c/m \(f\left(x\right)=x^2-ax-3bc+\dfrac{a^2}{3}>0\forall x\)
\(\Delta_{x_{a,b,c}}=a^2+12bc-\dfrac{4}{3}a^2=\dfrac{-a^2+36bc}{3}\)
\(\Delta=\dfrac{-a^3+36}{3a}\)
\(a^3>36\Rightarrow\left\{{}\begin{matrix}a>0\\-a^3+36< 0\end{matrix}\right.\) \(\Rightarrow\dfrac{-36a^3+36}{3a}< 0\)
\(\Rightarrow\) F(x) vô nghiệm => f(x)>0 với x => dpcm
b)
\(\dfrac{a^2}{3}+b^2+c^2>ab+bc+ca\)\(\Leftrightarrow\dfrac{a^2}{3}+b^2+c^2-ab-bc-ac>0\)
\(\Leftrightarrow\left(b+c\right)^2-a\left(b+c\right)-3bc+\dfrac{a^2}{3}>0\)
Từ (a) =>\(f\left(b+c\right)=\left(b+c\right)^2-a\left(b+c\right)-3bc+\dfrac{a^2}{3}>0\) => dccm