C thuộc Ox nên C(x;0)

CQ=8

=>\(CQ^2=8^2=64\)

=>\(\left(3-x\right)^2+\left(8-0\right)^2=64\)

=>\(\left(3-x\right)^2=0\)

=>3-x=0

=>x=3

=>C(3;0)

a: Tọa độ trung điểm I của AB là:

\(\left\{{}\begin{matrix}x=\dfrac{-1+2}{2}=\dfrac{1}{2}\\y=\dfrac{1+3}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)

=>I(1/2;2)

A(-1;1); B(2;3)

=>\(\overrightarrow{AB}=\left(2+1;3-1\right)\)

=>\(\overrightarrow{AB}=\left(3;2\right)\)

Gọi d là đường trung trực của AB

mà I là trung điểm của AB

nên d\(\perp\)AB tại I

d\(\perp\)AB nên d nhận \(\overrightarrow{AB}=\left(3;2\right)\) làm vecto pháp tuyến

Phương trình d là:

\(3\left(x-\dfrac{1}{2}\right)+2\left(y-2\right)=0\)

=>\(3x+2y-\dfrac{11}{2}=0\)

b: \(A\left(-1;1\right);C\left(1;4\right)\)

=>\(\overrightarrow{AC}=\left(1+1;4-1\right)=\left(2;3\right)\)

=>AC có vecto pháp tuyến là (-3;2)

Phương trình đường thẳng AC là:

-3(x+1)+2(y-1)=0

=>-3x-3+2y-2=0

=>-3x+2y-5=0

c: Tọa độ trung điểm M của AC là:

\(\left\{{}\begin{matrix}x=\dfrac{-1+1}{2}=\dfrac{0}{2}=0\\y=\dfrac{1+4}{2}=\dfrac{5}{2}\end{matrix}\right.\)

Xét ΔABC có

I,M lần lượt là trung điểm của AB,AC

=>IM là đường trung bình của ΔABC

=>IM//BC

I(1/2;2) M(0;5/2)

\(\overrightarrow{IM}=\left(0-\dfrac{1}{2};\dfrac{5}{2}-2\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)=\left(-1;1\right)\)

=>IM có vecto pháp tuyến là (1;1)

Phương trình đường trung bình ứng với cạnh BC là:

1(x-0)+1(y-5/2)=0

=>\(x+y-\dfrac{5}{2}=0\)

Đề ko đúng rồi em, dữ kiện cuối là góc thì phải có 3 điểm chứ

\(x^2-2x+m=0\Leftrightarrow x^2-2x-3=-m-3\)

Từ đồ thị ta thấy:

a.

Phương trình vô nghiệm khi \(-m-3< -4\Rightarrow m>1\)

b.

Phương trình có nghiệm kép khi \(-m-3=-4\Rightarrow m=1\)

c.

Phương trình có 2 nghiệm pb khi:

\(-m-3>-4\Rightarrow m< 1\)

d.

Phương trình có 2 nghiệm pb thuộc \(\left[-1;3\right]\) khi: \(-4< m\le0\)

e.

Có 2 nghiệm pb ko thuộc \(\left[-1;3\right]\) khi \(m>0\)

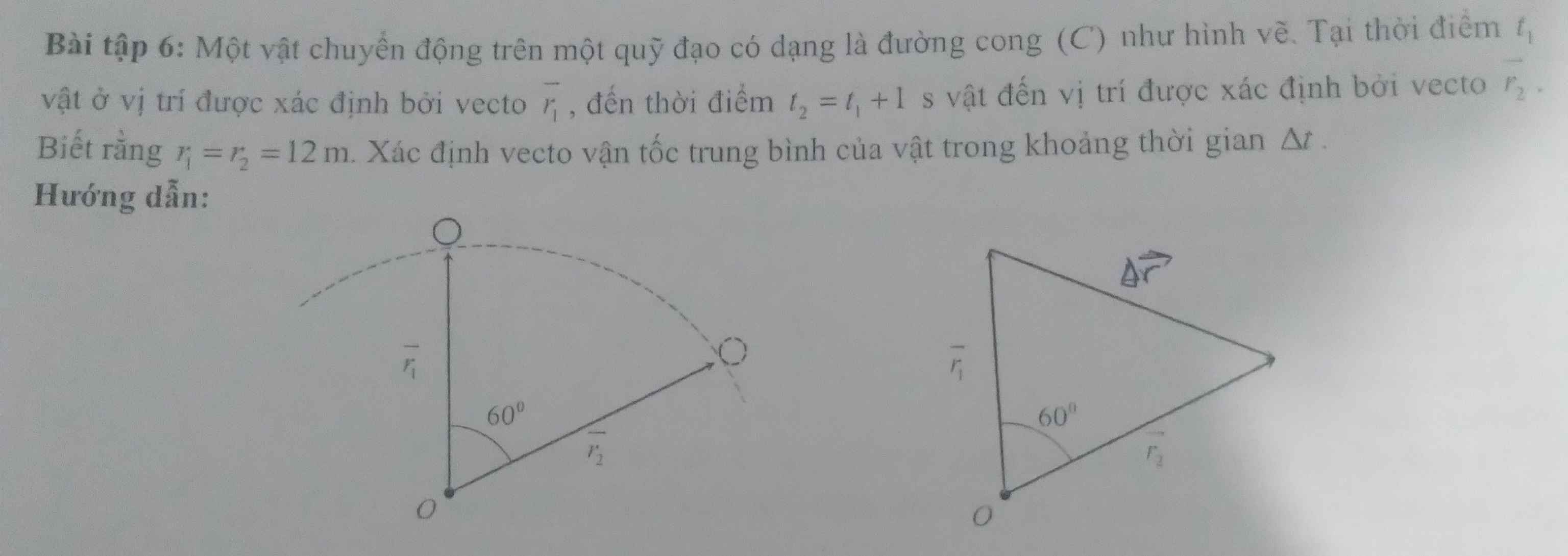
Vectơ vận tốc trung bình có phương và chiều trùng với vectơ độ dời

Độ lớn của vận tốc trung bình được tính như sau:

$|\overrightarrow{v_{tb}}|=\dfrac{|\overrightarrow{\Delta r}|}{\Delta t}=\dfrac{12}{1}=12$ (m/s)

(Do tam giác tạo bởi các vectơ $\overrightarrow{r_1},\,\overrightarrow{r_2},\,\overrightarrow{\Delta r}$ đều)

Em đăng kí nhận quà may mắn khảo sát

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}ab\cdot sinC=\dfrac{1}{2}\cdot7\cdot23\cdot sin130^o=61,7\) (đvdt)