b. ta có \(-x\left(x-2\right)+4=\left(x+1\right)\left(1-x\right)\Leftrightarrow-x^2+2x+4=1-x^2\)

\(\Leftrightarrow2x=-3\Leftrightarrow x=-\frac{3}{2}\)

c.\(16x^2=\left(x-1\right)^2\Leftrightarrow\orbr{\begin{cases}4x=x-1\\4x=1-x\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{1}{5}\end{cases}}}\)

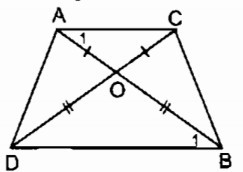
Ta có: OA = OC (gt)

⇒ Δ∆OAC cân tại O

⇒∠A1∠A1= (18001800 - ∠∠(AOC) ) / 2 (tính chất tam giác cân) (1)

OB = OD (gt)

⇒ Δ∆OBD cân tại O

⇒ ∠B1∠B1= (18001800 - ∠∠(BOD) )/2 (tính chất tam giác cân) (2)

∠∠(AOC) = ∠∠(BOD) (đối đỉnh) (3)

Từ (1), (2), (3) suy ra: ∠A1∠A1 = ∠B1∠B1

⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)

Suy ra: Tứ giác ACBD là hình thang

Ta có: AB = OA + OB

CD = OC + OD

Mà OA = OC, OB = OD

Suy ra: AB = CD

Vậy hình thang ABCD là hình thang cân.

Trả lời:

\(\frac{x+3}{4}=\frac{2-x}{5}\)

\(\Leftrightarrow\frac{5\left(x+3\right)}{20}=\frac{4\left(2-x\right)}{20}\)

\(\Leftrightarrow5\left(x+3\right)=4\left(2-x\right)\)

\(\Leftrightarrow5x+15=8-4x\)

\(\Leftrightarrow5x+4x=8-15\)

\(\Leftrightarrow9x=-7\)

\(\Leftrightarrow x=-\frac{7}{9}\)

Vậy x = - 7/9 là nghiệm của pt.

\(\frac{x+3}{4}=\frac{2-x}{5}\)

\(\Rightarrow\frac{5\left(x+3\right)}{20}=\frac{4\left(2-x\right)}{20}\)

\(\Rightarrow5\left(x+3\right)=4\left(2-x\right)\)

\(\Rightarrow5x+15=8-4x\)

\(\Rightarrow5x+4x=8-15\)

\(\Rightarrow9x=-1\Leftrightarrow x=\frac{-7}{9}\)

Vậy ............

Trả lời:

Ta có: \(x^2-6x+10=x^2-2.x.3+9+1=\left(x-3\right)^2+1\)

Lại có: \(\left(x-3\right)^2\ge0\forall x\)

\(\Leftrightarrow\) \(\left(x-3\right)^2+1\ge1\forall x\)

\(\Leftrightarrow\frac{5}{\left(x-3\right)^2+1}\le\frac{5}{1}=5\forall x\)

Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3

Vậy GTLN của A = 5 khi x = 3

\(n+13=a^2,n+33=b^2,\left(b>a\ge0;a,b\inℤ\right)\).

\(b^2-a^2=n+33-\left(n+13\right)=20\)

\(\Leftrightarrow\left(b+a\right)\left(b-a\right)=20\)

Có \(a,b\)là số nguyên nên \(b+a,b-a\)là các ước của \(20\)mà lại có \(\left(b+a\right)+\left(b-a\right)=2b\)là số chẵn nên \(b+a,b-a\)cùng tính chẵn lẻ, do đó ta chỉ có trường hợp: 

\(\hept{\begin{cases}b+a=10\\b-a=2\end{cases}}\Leftrightarrow\hept{\begin{cases}a=4\\b=6\end{cases}}\)

suy ra \(n=3\).

ta giả sử;

\(\hept{\begin{cases}a^2=n+13\\b^2=n+33\end{cases}\Rightarrow b^2-a^2=20}\) ha y \(\left(b-a\right)\left(b+a\right)=20\Rightarrow\orbr{\begin{cases}b-a=1\\b-a=2\end{cases}\text{ hoặc }b-a=4}\)

với \(\hept{\begin{cases}b-a=1\\b+a=20\end{cases}}\) hoặc \(\hept{\begin{cases}b-a=4\\b+a=5\end{cases}}\)mâu thuẫn với a,b là số tự nhiên 

với \(\hept{\begin{cases}b-a=2\\b+a=10\end{cases}\Leftrightarrow\hept{\begin{cases}b=6\\a=4\end{cases}\Rightarrow n=3}}\)

20% dd

?????????????????????????

1, \(5x^2+10x+5-5y^2=5\left(x^2+2x+1-y^2\right)\)

\(=5\left[\left(x+1\right)^2-y^2\right]=5\left(x+1-y\right)\left(x+1+y\right)\)

2, \(3x^3+6x^2+3x-12xy^2=3x\left(x^2+2x+1-4y^2\right)\)

\(=3x\left[\left(x+1\right)^2-4y^2\right]=3x\left(x+1-2y\right)\left(x+1+2y\right)\)