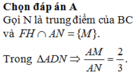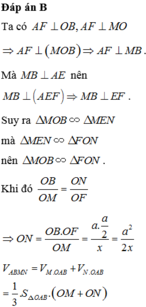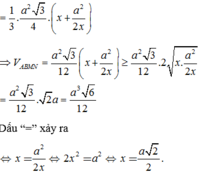Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do CM là trung tuyến của SAC nên M là trung điểm SA.
\(\dfrac{V_{SMBC}}{V_{SABC}}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Ta có \(AC=\sqrt{AB^2+AC^2}=a\sqrt{2}\) nên \(AH=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
Suy ra \(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-\dfrac{2a^2}{16}}=\dfrac{a\sqrt{14}}{4}\)
Do đó \(V_{SABC}=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{14}}{4}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{14}}{24}\)
Vậy \(V_{SMBC}=\dfrac{1}{2}V_{SABC}=\dfrac{a^3\sqrt{14}}{48}\)

Gọi P là trung điểm của SA. Ta có MNCP là hình bình hành nên MN song song với mặt phẳng (SAC). Mặt khác, BD vuông góc với mặt phẳng (SAC) nên BD vuông góc với MN.
Vì MN song song với mặt phẳng (SAC) nên
\(d\left(MN,AC\right)=d\left(N,SAC\right)\)
\(=\frac{1}{2}d\left(B;\left(SAC\right)\right)=\frac{1}{4}BD=\frac{a\sqrt{2}}{4}\)
Vậy \(d\left(MN;AC\right)=\frac{a\sqrt{2}}{4}\)

a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)