 giúp mình nha
giúp mình nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm số tự nhiên nhỏ nhất khi chia cho 6, 7, 9 được số dư theo thứ tự là 2, 3, 5
Gọi số đó là a
=>a=6x+2=>a+4=6x+6=6(x+1) chia hết cho 6
Tương tự a+4 cũng sẽ chia hết cho 7,9
Do a là số tự nhiên =>a+4>0
vậy nên ta chỉ cần tìm BCNN(6,7,9)=126
=>a=122
vậy a=122 là số cần tìm

a) aAc và bBA
b) Góc BAD đối đỉnh với góc aAc => Góc BAD = 123o
c) aAc kề bù cAD => cAD = 180o - 123o =57o
Hai góc đồng vị bằng nhau => Hai cạnh a và b song song
d) a // b mà a vuông góc d => b cũng vuông góc d
Nhớ ti.ckk cho mình nha

B = x15 - 8x14 + 8x13 - 8x2 + ... - 8x2 + 8x - 5
B = x^15 - 7x^14 -x^14+7x^13+x^13-7x^12-...-x^2+7x+x-5
B = x^14(x-7) - x^14(x-7) +...+x^2(x-7)-x(x-7)+x-5
B = 7-5=2
khoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooong


Vì số học sinh khi xếp 12 hàng, 15 hàng đều vừa đủ nên số học sinh của khối lứop 6 của trường đó là bội chung của 12 và 15
Ta có: 12=3.22
10=2.5
8=23
BCNN(8,10,12) = 23.3.5=120
BC(12,15) = B(120)={0;120;240;360....}
Do số học sinh năm trong khoảng từ 150 đến 200 học sinh nên số hoc sinh khối 6 của trường đó là 120học sinh
HT

a = 24/5,
b = 36/5,
c = 9;
tích mk nha
hok tốt
TL:
\(\dfrac{a}{2}=\dfrac{b}{3}\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}\)
\(\dfrac{b}{5}=\dfrac{c}{4}\Rightarrow\dfrac{b}{15}=\dfrac{c}{12}\)
\(\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{12}=\dfrac{a-b+c}{10-15+12}=\dfrac{21}{7}=3\)
\(\dfrac{a}{10}=3\Rightarrow a=30\\ \dfrac{b}{15}=3\Rightarrow b=45\\ \dfrac{c}{12}=3\Rightarrow c=36\)
^HT^

TKL:
1) Tách S=1+(10+1)+(100+10+1)+(1000+100+10+1)+
(10000+1000+100+10+1)+...
S=10*1+9*10+8*100+7*10^3+6*10^4+
5*10^5+4*10^6+3*10^7+2*10^8+10^9
S=1234567900
2)Tổng sáu số đầu là 81 mới đúng!Nếu đây là dãy cộng thì ta có thể giải được.
Gọi hiệu 2 số liên tiếp của dãy là d.
Ta có công thức tính số hạng thứ n của dãy: a(n)=a(1)+(n-1)*d
^HT^
 giúp mình với
giúp mình với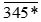 :
:
a) \(2x\left(x-7\right)+5\left(x-7\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-7\right)=0\)
\(\Leftrightarrow x=\frac{-5}{2},x=7\)
b) \(x^3-2x^2+x-2=0\)
\(\Leftrightarrow x^2\left(x-2\right)+\left(x-2\right)=0\)
\(=\left(x^2+1\right)\left(x-2\right)=0\)
Vậy x = 2