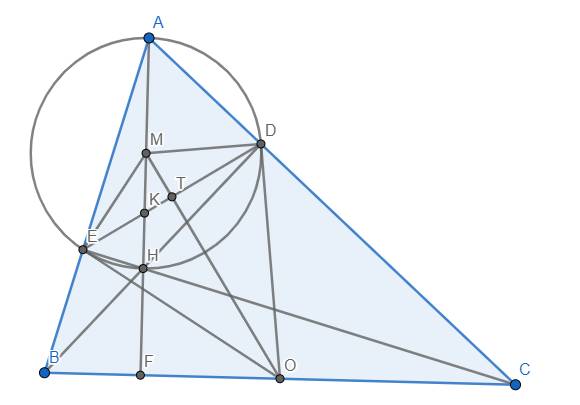
c) Dễ thấy M, O là tâm của đường tròn (ADHE) và (BEDC). Gọi bán kính của đường tròn (ADHE) là \(R\)

 Gọi T là giao điểm của OM và DE.

 Ta thấy vì \(OD=OE,MD=ME\) nên OM là trung trực của DE \(\Rightarrow OM\perp DE\) tại T

 Xét tam giác MTK và MFO, có:

 \(\widehat{FMO}\) chung, \(\widehat{MTK}=\widehat{MFO}=90^o\)

 \(\Rightarrow\Delta MTK~\Delta MFO\left(g.g\right)\)

 \(\Rightarrow\dfrac{MT}{MF}=\dfrac{MK}{MO}\)

 \(\Rightarrow MT.MO=MF.MK\)

 Tam giác MDO vuông tại D có đường cao DT nên \(MT.MO=MD^2\)

 \(\Rightarrow MF.MK=MD^2\) \(=R^2\)

 \(\Rightarrow MK=\dfrac{R^2}{MF}\) \(=\dfrac{R^2}{R+HF}\)

Do đó \(VP=2MK\left(AF+HF\right)\)

\(=\dfrac{2R^2}{R+HF}\left(2R+2HF\right)\) (thế \(AF=AH+HF=2R+HF\))

\(=4R^2\)

\(=AH^2=VT\)

Vậy ta có đpcm.

a) Nhận thấy \(\widehat{OBK}=\widehat{OAK}=90^o\) \(\Rightarrow\) Tứ giác OAKB nội tiếp đường tròn (OK).

Mặt khác \(\widehat{OHK}=90^o\) nên \(H\in\left(OK\right)\)

\(\Rightarrow\) 5 điểm A, B, O, K, H cùng thuộc đường tròn (OK).

b) Từ câu a) \(\Rightarrow\) Tứ giác OAHB nội tiếp 

\(\Rightarrow\widehat{IHB}=\widehat{IAO}\)

Từ đó dễ dàng chứng minh \(\Delta IHB~\Delta IAO\left(g.g\right)\)

\(\Rightarrow\dfrac{IH}{IA}=\dfrac{IB}{IO}\) \(\Rightarrow IA.IB=IH.IO\) (đpcm)

c) Gọi T là giao điểm của OK và AB.

Tính chất của 2 tiếp tuyến cắt nhau \(\Rightarrow OK\perp AB\) tại T

Tam giác OAK vuông tại A có đường cao AT nên \(OT.OK=OA^2\) (hệ thức lượng trong tam giác vuông)

Xét tam giác OTI và OHK, ta có:

\(\widehat{HOK}\) chung , \(\widehat{OTI}=\widehat{OHK}=90^o\)

 \(\Rightarrow\Delta OTI~\Delta OHK\left(g.g\right)\)

 \(\Rightarrow\dfrac{OT}{OH}=\dfrac{OI}{OK}\)

 \(\Rightarrow OT.OK=OH.OI\)

Mà \(OT.OK=OA^2\) (cmt) \(\Rightarrow OH.OI=OA^2\)

\(\Rightarrow OI=\dfrac{OA^2}{OH}\) là một hằng số 

\(\Rightarrow\) I thuộc đường tròn \(\left(O;\dfrac{OA^2}{OH}\right)\) cố định

Hơn nữa I nằm trên đường thẳng OH cố định nên I cố định

\(\Rightarrow\) AB đi qua I cố định.

Ta có \(VT=\dfrac{\dfrac{4x^2}{y^2}}{\left(\dfrac{x^2}{y^2}+1\right)^2}+\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\)

Đặt \(\dfrac{x^2}{y^2}=t\left(t>0\right)\) thì VT thành

\(\dfrac{4t}{\left(t+1\right)^2}+t+\dfrac{1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{t^2+1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{\left(t+1\right)^2}{t}-2\)

Đặt \(\dfrac{\left(t+1\right)^2}{t}=u\left(u\ge4\right)\) (vì BĐT \(\left(a+b\right)^2\ge4ab\))

Khi đó \(VT=u+\dfrac{4}{u}-2\)

 \(=\dfrac{4}{u}+\dfrac{u}{4}+\dfrac{3u}{4}-2\)

\(\ge2\sqrt{\dfrac{4}{u}.\dfrac{u}{4}}+\dfrac{3.4}{4}-2\)

\(=2+3-2\)

\(=3\)

\(\Rightarrow VT\ge3\)

Dấu "=" xảy ra \(\Leftrightarrow u=4\) \(\Leftrightarrow t=1\) \(\Leftrightarrow x=\pm y\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x=\pm y\)

Bài 6: 

Ta có \(A=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2023^2}\)

\(A< 1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2022.2023}\)

\(A< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)

\(A< 2\)

Lại có \(A>1\) nên A không phải là số tự nhiên.

Bài 7:

 Xét tập hợp \(A=\left\{x\inℕ|2^x\le29\right\}\). Vì A có hữu hạn phần tử nên A có phần từ lớn nhất. Gọi phần tử lớn nhất đó là \(\alpha\). Gọi \(a\) là tích của tất cả các số lẻ không vượt quá 29. Xét số \(b=2^{\alpha-1}.a\). Ta có \(b\) là bội của tất cả các phần tử của tập hợp \(\left\{2;3;4;...;29\right\}\backslash\left\{2^{\alpha}\right\}\). Do đó:

 \(b.B=\dfrac{b}{2}+\dfrac{b}{3}+...+\dfrac{b}{2^{\alpha}}+...+\dfrac{b}{29}\notinℕ\)

  Vậy B không là số tự nhiên.

Bài 8: 

a) Làm giống bài 7.

b) 

Bạn viết rõ ra xem dạng này là gì nhé.

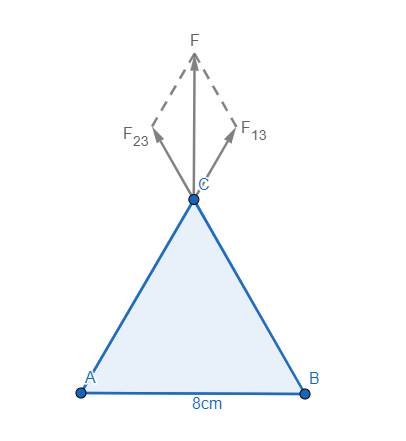
a) Ta có \(F_{13}=\dfrac{k\left|q_1q_3\right|}{AC^2}\) \(=\dfrac{9.10^9\left|6.10^{-6}.4.10^{-6}\right|}{\left(0,08\right)^2}\) \(=33,75\left(N\right)\)

Đồng thời \(F_{13}=F_{23}\) do \(q_1=q_2\)

\(\Rightarrow F=\sqrt{F_{13}^2+F_{23}^2+2F_{13}F_{23}\cos\left(\overrightarrow{F_{13}},\overrightarrow{F_{23}}\right)}\)

\(=\sqrt{33,75^2+33,75^2+2.33,75.33,75\cos60^o}\)

\(\approx58,46\left(N\right)\)

 Vậy vector lực điện do 2 điện tích q₁, q₂ tác dụng lên q₃ là một vector có giá trùng với đường trung trực của AB và có độ lớn khoảng \(58,46N\)

Dạ thì khi đó BĐT thành \(\dfrac{2021\left(-\dfrac{2020}{2021}\right)+2023}{\sqrt{1-\left(-\dfrac{2020}{2021}\right)^2}}\ge2\sqrt{2022}\)

\(\Leftrightarrow\dfrac{3}{\sqrt{\dfrac{2021^2-2020^2}{2021^2}}}\ge2\sqrt{2022}\)

\(\Leftrightarrow\dfrac{6063}{\sqrt{4041}}\ge2\sqrt{2022}\)

\(\Leftrightarrow2\sqrt{2022.4041}\le6063\)

\(\Leftrightarrow2\sqrt{2694.3033}\le6063\)

Mà \(2\sqrt{2694.3033}\le2694+3033=5727< 6063\) nên BĐT vẫn đúng ạ.

Đk: \(-1< x< 1\)

Ta có \(2\sqrt{2022\left(1-x^2\right)}\le2023-x^2\) 

Nếu \(0\le x< 1\) thì \(x\left(x+2021\right)\ge0\) 

\(\Leftrightarrow x^2+2021x\ge0\)

\(\Leftrightarrow2023-x^2\le2021x+2023\)

\(\Rightarrow\) \(2\sqrt{2022\left(1-x^2\right)}\le2023-x^2\le2021x+2023\)

\(\Leftrightarrow2\sqrt{2022}\le\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}2022=1-x^2\\x=0\end{matrix}\right.\), vô lý.

Vậy nếu \(0\le x< 1\) thì BĐT đúng.

Xét \(-1< x< 0\) thì đặt \(x=-t\left(0< t< 1\right)\). 

BĐT cần chứng minh \(\Leftrightarrow\dfrac{2023-2021t}{\sqrt{1-t^2}}\ge2\sqrt{2022}\)

Ta có \(2023-2021t\) 

\(=2022-2022t+1+t\)

\(=2022\left(1-t\right)+\left(1+t\right)\)

\(\ge2\sqrt{2022\left(1-t\right)\left(1+t\right)}\)

\(=2\sqrt{2022\left(1-t^2\right)}\)

\(\Leftrightarrow\dfrac{2023-2021t}{\sqrt{1-t^2}}\ge2\sqrt{2022}\)

Dấu "=" xảy ra \(\Leftrightarrow2022-2022t=1+t\) \(\Leftrightarrow t=\dfrac{2021}{2023}\) \(\Leftrightarrow x=-\dfrac{2021}{2023}\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{2021}{2023}\)

 Với lại bạn cần loại nghiệm \(x=y=0\) nhé vì nó không thỏa mãn pt (1).

\(\left\{{}\begin{matrix}8x^3y^3+27=18y^3\left(1\right)\\4x^2y+6x=y^2\left(2\right)\end{matrix}\right.\)

pt (2) \(\Leftrightarrow4x^2y^2+6xy=y^3\) (3)

Thế (3) vào (1), ta được \(8x^3y^3+27=18\left(4x^2y^2+6xy\right)\)

\(\Leftrightarrow8\left(xy\right)^3-72\left(xy\right)^2-108xy+27=0\) (4)

Đặt \(xy=t\) thì (4) thành

\(8t^3-72t^2-108t+27=0\)

\(\Leftrightarrow8t^3+12t^2-84t^2-126t+18t+27=0\)

\(\Leftrightarrow4t^2\left(2t+3\right)-42t\left(2t+3\right)+9\left(2t+3\right)=0\)

\(\Leftrightarrow\left(2t+3\right)\left(4t^2-42t+9\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{3}{2}\\t=\dfrac{21\pm9\sqrt{5}}{4}\end{matrix}\right.\)

Xét \(t=-\dfrac{3}{2}\) \(\Rightarrow xy=-\dfrac{3}{2}\) . Thay vào (2), ta có:

\(y^3=4\left(xy\right)^2+6xy\) \(=4\left(-\dfrac{3}{2}\right)^2+6\left(-\dfrac{3}{2}\right)=0\)  

\(\Leftrightarrow y=0\) \(\Leftrightarrow x=0\)

Nếu \(t=\dfrac{21+9\sqrt{5}}{4}\) thì \(xy=\dfrac{21+9\sqrt{5}}{4}\). Thay vào (2), ta có:

\(y^3=4\left(\dfrac{21+9\sqrt{5}}{4}\right)^2+6\left(\dfrac{21+9\sqrt{5}}{4}\right)\) \(\Rightarrow y=...\Rightarrow x=...\)

Xét tương tự với \(t=\dfrac{21-9\sqrt{5}}{4}\)

Vậy ...

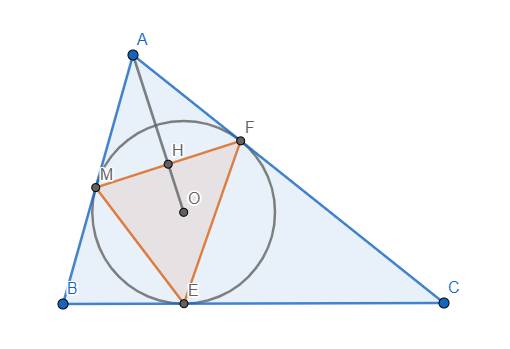
Gọi H là giao điểm của FM và OA.

Tính được \(AM=\dfrac{b+c-a}{2}\)

Tính được \(cos\widehat{BAC}=\dfrac{b^2+c^2-a^2}{2bc}\) rồi dùng 

\(MF=\sqrt{AM^2+AF^2-2AM.AF.cos\widehat{BAC}}\)

 \(=\sqrt{2AM^2\left(1-cos\widehat{BAC}\right)}\) 

 \(=MA\sqrt{2\left(1-\dfrac{b^2+c^2-a^2}{2bc}\right)}\)

 \(=MA\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

 \(=\dfrac{b+c-a}{2}\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

\(\Rightarrow\dfrac{MF}{MA}=\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}=J\)

\(\Rightarrow cos\widehat{MEF}=cos\widehat{MAH}=\dfrac{MH}{MA}=\dfrac{J}{2}\)

\(\Rightarrow sin\widehat{MEF}=\sqrt{1-cos^2\widehat{MAH}}\)

 \(=\sqrt{1-\dfrac{J^2}{4}}\) 

 \(=\sqrt{1-\dfrac{a^2-b^2-c^2+2bc}{4bc}}\)

 \(=\sqrt{\dfrac{\left(b+c\right)^2-a^2}{4bc}}\) \(=A\)

Ta cũng tính được \(ME=\dfrac{c+a-b}{2}\sqrt{\dfrac{b^2-\left(c-a\right)^2}{ca}}=\dfrac{c+a-b}{2}\sqrt{\dfrac{\left(b+c-a\right)\left(a+b-c\right)}{ca}}\)

\(EF=\dfrac{a+b-c}{2}\sqrt{\dfrac{c^2-\left(a-b\right)^2}{ab}}=\dfrac{a+b-c}{2}\sqrt{\dfrac{\left(c+a-b\right)\left(b+c-a\right)}{ab}}\)

\(\Rightarrow S_{MEF}=\dfrac{1}{2}EM.EF.sin\widehat{MEF}\) \(=...\)