

Lê Song Phương
Giới thiệu về bản thân



































TH1: Trong 4 bi được chọn có đủ 3 màu, trong đó có 2 bi màu xanh: Có 6 cách chọn bi xanh thứ nhất, 5 cách chọn bi xanh thứ hai, 7 cách chọn bi đỏ, 8 cách chọn bi vàng \(\Rightarrow\) Có \(6.5.7.8=1680\) cách. Nhưng vì đếm theo cách này, mỗi cách chọn bi phân biệt sẽ bị lặp lại \(4!=24\) lần nên có tất cả \(\dfrac{1680}{24}=70\) cách chọn phân biệt.
TH2: Trong 4 bi được chọn có đủ 3 màu, trong đó có 2 bi màu đỏ: Có 7 cách chọn bi đỏ thứ nhất, 6 cách chọn bi đỏ thứ hai, 6 cách chọn bi xanh, 8 cách chọn bi vàng \(\Rightarrow\) Có \(7.6.6.8=2016\) cách \(\Rightarrow\)Có tất cả \(\dfrac{2016}{24}=84\) cách chọn phân biệt.
TH3: Trong 4 bi được chọn có đủ 3 màu, trong đó có 2 bi màu vàng: Có 8 cách chọn bi vàng thứ nhất, 7 cách chọn bi vàng thứ hai, 6 cách chọn bi xanh, 7 cách chọn bi đỏ \(\Rightarrow\) Có \(8.7.6.8=2688\) cách \(\Rightarrow\)Có tất cả \(\dfrac{2688}{24}=112\) cách chọn phân biệt.
Vậy có tất cả \(70+84+112=266\) cách chọn.
Câu 1:
a) \(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}.10.8^2=320\left(m\right)\)
\(v_{đất}=gt=10.8=80\left(m/s\right)\)
b) Quãng đường vật đi được sau 7 giây là:
\(h'=\dfrac{1}{2}gt^2=\dfrac{1}{2}.10.7^2=245\left(m\right)\)
Quãng đường vật đi được trong giây cuối cùng là:
\(\Delta h=h-h'=320-245=75\left(m\right)\)
Câu 2:
Hình vẽ 2 của bạn ở đâu mình không thấy nhỉ?
c) Nếu \(x,y\) cùng lẻ thì VT chẵn, VP lẻ, vô lý. Nếu cả 2 số \(x,y\) cùng chẵn thì VT lẻ, VP chẵn, cũng vô lý. Vậy trong 2 số \(x,y\) phải có 1 số chẵn và 1 số lẻ.
TH1: \(x\) chẵn, \(y\) lẻ. Do \(x\) là số nguyên tố nên \(x=2\) \(\Rightarrow19y^2=13\), vô lý.
TH2: \(y\) chẵn, \(x\) lẻ. Do \(y\) là số nguyên tố nên \(y=2\Rightarrow3x^2+1=76\)
\(\Leftrightarrow x=5\), thỏa mãn.
Vậy ta tìm được bộ số \(\left(x;y\right)=\left(2;5\right)\) thỏa mãn yêu cầu bài toán.
Chỗ kia phải là \(\dfrac{c^4}{b+a+4ba}\) chứ nhỉ? Nếu đúng đề thì bạn nói với mình để mình làm lại nhé. Giờ mình làm theo đề đối xứng trước nhé.
Ta có:
\(P=\dfrac{a^6}{a^2b+a^2c+4a^2bc}+\dfrac{b^6}{b^2a+b^2c+4b^2ca}+\dfrac{c^6}{c^2a+c^2b+4c^2ab}\)
\(\ge\dfrac{\left(a^3+b^3+c^3\right)^2}{a^2b+b^2c+c^2a+ab^2+bc^2+ca^2+4a^2bc+4b^2ca+4c^2ab}\)
\(=\dfrac{9}{\left(a+b+c\right)\left(ab+bc+ca\right)+abc\left(4\left(a+b+c\right)-3\right)}\)
Ta có \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}\)
và \(abc\le\dfrac{a^3+b^3+c^3}{3}=1\), đồng thời \(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)>\dfrac{27}{64}\)
\(\Leftrightarrow a+b+c>\dfrac{3}{4}\) \(\Leftrightarrow4\left(a+b+c\right)-3>0\). Do đó \(abc\left(4\left(a+b+c\right)-3\right)\le4\left(a+b+c\right)-3\)
Vì vậy \(P\ge\dfrac{9}{\dfrac{\left(a+b+c\right)^3}{3}+4\left(a+b+c\right)-3}\)
Đặt \(a+b+c=t\).
Ta có \(a^3+b^3\ge ab\left(a+b\right)=a^2b+b^2a\). Lập 2 BĐT tương tự rồi cộng theo vế, ta có:
\(2\left(a^3+b^3+c^3\right)\ge a^2b+b^2c+c^2a+ab^2+bc^2+ca^2\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\le6+2abc\le8\) (vì \(abc\le1\))
Do đó \(t^3=3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\le3+3.8=27\) \(\Leftrightarrow t\le3\)
Vậy \(0< t\le3\)
Ta có \(P\ge\dfrac{9}{\dfrac{t^3}{3}+4t-3}\) \(\ge\dfrac{9}{\dfrac{3^3}{3}+4.3-3}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Vậy GTNN của P là \(\dfrac{1}{2}\) khi \(a=b=c=1\)
Câu 14:
a) \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{2-\sqrt{2-x}}{x+2}=\dfrac{2-\sqrt{2-1}}{1+2}=f\left(1\right)\) => Khẳng định đúng.
b) \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\left(x^2+ax+2\right)=+\infty\) => Khẳng định sai.
c) \(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=\lim\limits_{x\rightarrow-2^+}\dfrac{2-\sqrt{2-x}}{x+2}\) \(=\lim\limits_{x\rightarrow-2^+}\dfrac{4-\left(2-x\right)}{\left(x+2\right)\left(2+\sqrt{2-x}\right)}\)
\(=\lim\limits_{x\rightarrow-2^+}\dfrac{1}{2+\sqrt{2-x}}\) \(=\dfrac{1}{2+\sqrt{2-\left(-2\right)}}=\dfrac{1}{4}\)
=> Khẳng định đúng.
d) Ta có \(\lim\limits_{x\rightarrow-2^+}f\left(x\right)=\dfrac{1}{4}\) và \(\lim\limits_{x\rightarrow-2^-}f\left(x\right)=\lim\limits_{x\rightarrow-2^-}\left(x^2+ax+2\right)=4-2a+2\)
Để tồn tại \(\lim\limits_{x\rightarrow-2}f\left(x\right)\) thì \(4-2a+2=\dfrac{1}{4}\) \(\Leftrightarrow a=\dfrac{23}{8}\)
Có \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{2-\sqrt{2-x}}{x+2}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+a-b\right)=2+a-b\)
Để tồn tại \(\lim\limits_{x\rightarrow2}f\left(x\right)\) thì \(2+a-b=\dfrac{1}{2}\) \(\Leftrightarrow b=a+\dfrac{3}{2}=\dfrac{35}{8}\)
Khi đó \(4\left(a+b\right)=4\left(\dfrac{23}{8}+\dfrac{35}{8}\right)=29\)
=> Khẳng định đúng
Câu 13:
Ta có công thức lãi kép: \(C=A\left(1+r\right)^N\) với C là số tiền thu được (cả vốn lẫn lãi); A là số tiền gửi; r là lãi suất mỗi kì, N là số kì.
a) Sau 2 năm số tiền cả vốn lẫn lãi ở quyển 1 là \(100\left(1+6,8\%\right)^2=114,0624\approx114\) (triệu đồng)
\(\Rightarrow\) Khẳng định đúng
b) Sau 2 năm số tiền cả vốn lẫn lãi ở quyển 2 là \(100\left(1+6\%\right)^2=112,36\) (tr đồng)
Suy ra số tiền ở cả 2 quyển là \(114,0624+112,36=226,4224\) (tr đồng)
\(\Rightarrow\) Khẳng định đúng.
c) Số tiền gửi sau \(N\) năm (kì) là:
\(C=100\left(1+6,8\%\right)^N+100\left(1+6\%\right)^N\)
Thế \(N\ge8\), ta có \(C\ge100\left[\left(1+6.8\%\right)^8+\left(1+6\%\right)^8\right]\approx328,65>300\)
\(\Rightarrow\) Khẳng định đúng.
d) Ta nhắc lại rằng nếu theo ban đầu, sau 2 năm thì số tiền thu được sẽ là \(226,4224\) tr đồng.
Theo tình huống mới, số tiền sau năm đầu ở quyển 1, 2 lần lượt là \(114,0624\) tr đồng và \(112,36\) tr đồng. Sau khi lấy 1 nửa số tiền từ đây chuyển sang quyển 2 thì lúc này quyển 1 còn \(57,0312\) tr đồng và quyển 2 có \(169,3912\) tr đồng. Sau năm thứ 2, quyển 1 có \(57,0312\left(1+6,8\%\right)=60,9093216\) (tr đồng), quyển 2 có \(169,3912\left(1+6\%\right)=179,554672\) (tr đồng). Do vậy cả 2 quyển có \(179,554672+60,9093216=240,4639936\) (tr đồng)
\(\Rightarrow\) Khẳng định đúng.
Ta có \(2006^{2024}=\left(7.286+4\right)^{2024}\) \(=7A+4^{2024}\). Do đó ta chỉ cần tìm số dư của \(4^{2024}\) khi chia cho 7.
Để ý rằng: \(4^0\equiv1\left[7\right]\); \(4^1\equiv4\left[7\right]\); \(4^2\equiv2\left[7\right]\); \(4^3\equiv1\left[7\right]\); \(4^4\equiv4\left[7\right]\); \(4^5\equiv2\left[7\right]\)
Do đó ta nảy sinh dự đoán rằng \(4^{3k+2}\equiv2\left[7\right]\left(k\inℕ\right)\). Ta sẽ chứng minh điều này bằng phương pháp quy nạp,
Thật vậy, với \(k=0\) thì khẳng định đúng (theo như trên)
Giả sử khẳng định đúng đến \(k=l\ge0\), khi đó \(4^{3l+2}\equiv2\left[7\right]\). Ta cần chứng minh khẳng định đúng với \(k=l+1\), tức là cm \(4^{3\left(l+1\right)+2}\equiv2\left[7\right]\)
Thật vậy, ta có \(4^{3\left(l+1\right)+2}\equiv4^{3l+3+2}\equiv64.4^{3l+2}\equiv1.2\equiv2\left[7\right]\)
Vậy khẳng định đúng với \(k=l+1\Rightarrow4^{3k+2}\equiv2\left[7\right]\)
Vì vậy \(4^{2024}=4^{2022+2}=4^{3.674+2}\equiv2\left[7\right]\)
Vậy số dư của phép chia \(2006^{2024}\) cho 7 là 2.
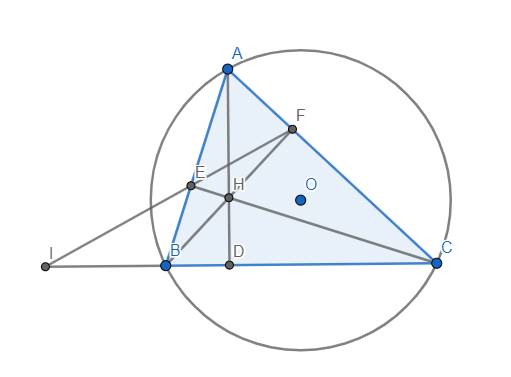
a) Ta có \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn (BC).
b) Tứ giác BEFC nội tiếp \(\Rightarrow\widehat{AEF}=\widehat{ACB}\)
Tam giác ABC và AFE có:
\(\widehat{A}\) chung, \(\widehat{AEF}=\widehat{ACB}\)
\(\Rightarrow\Delta ABC\sim\Delta AFE\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\)
\(\Rightarrow AB.AE=AF.AC\)
c) Áp dụng định lý Ceva cho tam giác ABC, ta được:
\(\dfrac{DB}{DC}.\dfrac{FC}{FA}.\dfrac{EA}{EB}=1\) (1)
Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến FEI, ta có:
\(\dfrac{IB}{IC}.\dfrac{FC}{FA}.\dfrac{EA}{EB}=1\) (2)
Từ (1) và (2), suy ra \(\dfrac{DB}{DC}=\dfrac{IB}{IC}\), ta có đpcm.
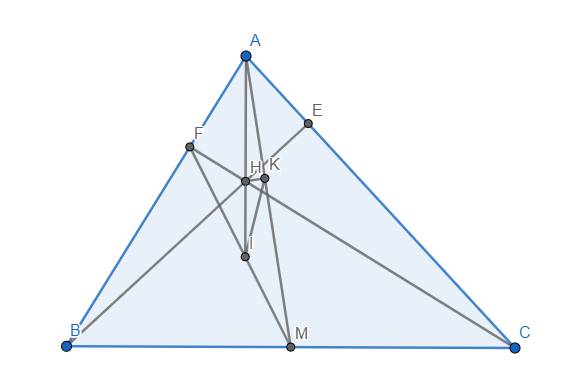
Nếu bạn nhìn trong hình này thì nó có phải là phân giác đâu?
Một cách "đơn giản" và "ngây thơ", ta thấy mỗi chữ số đều có 10 cách chọn (từ 0 đến 9) nên có tất cả \(10^4=10000\) biển số.
Tuy nhiên, ngoài lề một chút thì nếu theo đúng luật giao thông, kể cả mã tỉnh (từ 11 đến 99 - có 89 mã; và 2 kí tự seri, mỗi kí tự có thể là một trong 20 chữ cái in hoa sau: A, B, C, D, E, F, G, H, K, L, M, N, P, S, T, U, V, X, Y, Z. Chưa kể là còn có 4 loại màu biển số xe (trắng, xanh, đỏ, vàng) và mỗi loại biển số có quy định tạo biển số xe khác nhau nên lúc này số biển số sẽ tăng lên gấp rất nhiều lần, lưu ý là không tồn tại biển số xe 0000 nếu đăng ký đúng pháp luật)

