🔺Đề thi thử số 1 (phần tự luận) SVIP

Hướng dẫn giải:

a) Cho hai tập khác rỗng $A=(m-1 ; 4]$ và $B=(-2 ; 2 m+2)$ với $m \in \mathbb{R}$. Xác định $m$ để $A \cap B \neq \varnothing$.

Điều kiện: $\left\{\begin{aligned}&m-1<4 \\ &-2<2 m+2\\ \end{aligned} \Leftrightarrow-2<m<5\right.$.

Ta có $A \cap B=\varnothing \Leftrightarrow\left[\begin{aligned}&2 m+2 \leq m-1 \\ &4 \leq-2\\ \end{aligned} \Leftrightarrow m \leq-3\right.$.

Vậy $A \cap B \neq \varnothing \Leftrightarrow\left\{\begin{aligned}&-2<m<5 \\ &m>-3\\ \end{aligned} \Leftrightarrow-2<m<5\right.$.

b) Cho hai tập hợp $A=(m-1 ; 5]$ và $B=(3 ; 2020-5 m)$; $A$, $B$ khác rỗng. Có bao nhiêu giá trị nguyên của $m$ để $A \backslash B=\varnothing$?

Vì $A$, $B$ là hai tập hợp khác rỗng, nên ta có điều kiện: $\left\{\begin{aligned} &m - 1 < 5 \\ &3 < 2020 - 5m\\ \end{aligned} \Leftrightarrow \left\{\begin{aligned} &m<6 \\ &m<\dfrac{2017}{5}\\ \end{aligned} \Leftrightarrow m<6 .\right.\right.$ (*)

Để $A \backslash B=\varnothing$ thì $A \subset B$ ta có điều kiện: $\left\{\begin{aligned}&3 \leq m-1 \\ &5<2020-5 m\\ \end{aligned} \Leftrightarrow\left\{\begin{aligned}&4 \leq m \\ &m<403\\ \end{aligned} \Leftrightarrow 4 \leq m<403\right.\right.$.

Kết hợp điều kiện (*) ta được $4 \leq m<6$.

Vậy có $2$ giá trị nguyên của $m$ thỏa mãn yêu cầu.

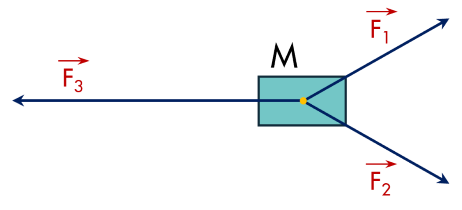
Hướng dẫn giải:

Vật đứng yên là do $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}$.

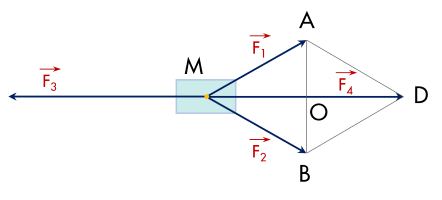
Vẽ hình thoi $M A D B$, ta có $\overrightarrow{F}_1+\overrightarrow{F_2}=\overrightarrow{M D}$ và lực $\overrightarrow{F}_4=\overrightarrow{M D}$ có cường độ lực là $25 \sqrt{3}$ N.

Ta có $\overrightarrow{F_3}+\overrightarrow{F_4}=\overrightarrow{0}$, do đó $\overrightarrow{F_3}$ là vectơ đối của $\overrightarrow{F}_4$.

Như vậy $\overrightarrow{F}_3$ có cường độ là $25 \sqrt{3}$ N và ngược hướng với $\overrightarrow{F_4}$.

Hướng dẫn giải:

Gọi $x$ là số xe loại $A$ ($0 \leq x \leq 10$; $x \in \mathbb{N})$ và $y$ là số xe loại $B$ ($0 \leq y \leq 9$; $y \in \mathbb{N})$.

Khi đó tổng chi phí thuê xe là $T=4 x+3 y$ (triệu đồng).

Xe $A$ chở tối đa $20$ người, xe $B$ chở tối đa $10$ người nên tổng số người hai xe chở tối đa được là $20 x+10 y$ (người).

Xe $A$ chở được $0,6$ tấn hàng, xe $B$ chở được $1,5$ tấn hàng nên tổng lượng hàng hai xe chở được là $0,6 x+1,5 y$ (tấn).

Theo giả thiết, ta có $\left\{\begin{aligned}&0 \leq x \leq 10 \\ &0 \leq y \leq 9 \\ &20 x+10 y \geq 140 \\ &0,6 x+1,5 y \geq 9\\ \end{aligned}\right.$ (*)

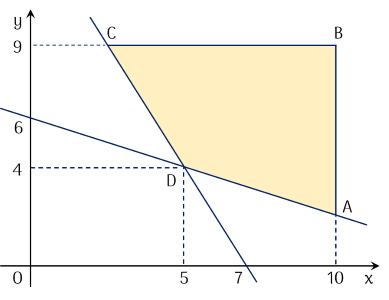
Biểu diễn miền nghiệm của hệ bất phương trình $(*)$ là tứ giác $A B C D$ kể cả miền trong của tứ giác.

Biểu thức $T=4 x+3 y$ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác $A B C D$.

Tại các đỉnh $A(10 ; 2)$; $B(10 ; 9)$; $C\left(\dfrac{5}{2} ; 9\right)$; $D(5 ; 4)$, ta thấy $T$ đạt giá trị nhỏ nhất tại $\left\{\begin{aligned}&x=5 \\ &y=4\\ \end{aligned}\right.$.

Khi đó $T_{\min }=32$.

Hướng dẫn giải:

Ta có: $ \overrightarrow{C M}. \overrightarrow{C B}=\overrightarrow{C M}^2 \Leftrightarrow \overrightarrow{C M} .(\overrightarrow{C M}+\overrightarrow{M B})=\overrightarrow{C M}^2 \Leftrightarrow \overrightarrow{C M}^2+\overrightarrow{C M} .\overrightarrow{M B}=\overrightarrow{C M}^2 \Leftrightarrow \overrightarrow{C M} \overrightarrow{M B}=0 $

$\Leftrightarrow \overrightarrow{C M} \perp \overrightarrow{M B}$ hay $C M \perp M B$.

Vậy tâp hợp những điểm $M$ thuộc đường tròn đường kính $BC$.