Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

🔹Ôn tập học kì I: phần Đại số SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Những câu nào sau đây là mệnh đề chứa biến?
Mệnh đề "∀x∈ R , x2>0" phát biểu thành lời là
Cho mệnh đề A: "2 là số nguyên tố" . Mệnh đề phủ định của mệnh đề A là
Cho tập hợp D. Mệnh đề nào sau đây sai?
Cho tập X={0;1;2;3;4;5} và tập A={0;2;4}. Phần bù của A trong X là
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp A={x∈R7≤x≤10}.
Miền nghiệm của bất phương trình 3(x−1)+4( y−2)<5x−3 là nửa mặt phẳng chứa điểm nào sau đây?
Cho hệ bất phương trình {x+3y−2≥02x+y+1≤0. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình trên?
Có hai bạn cùng nhau tìm đường chéo của hình chữ nhật có chiều dài là 5 cm, chiều rộng là 3 cm.
Bạn thứ nhất sử dụng thước kẻ học sinh (chính xác đến mm) dựng hình chữ nhật và đo được kết quả 5,8 cm.
Bạn thứ hai áp dụng định lí Py - ta - go, bạn tính được đường chéo của hình chữ nhật là 34 cm.
| Trong hai kết quả trên, | kết quả đúng là cm; |
| kết quả gần đúng là cm. |
(Kéo thả hoặc click vào để điền)
Tính các tứ phân vị cho dữ liệu về diện tích đất (đơn vị: km2 ) của 266 quốc gia và vùng lãnh thổ cho số liệu như sau:
Q1=20 574,1 ; Q2=194 690 ; Q3=1 249 825.
Diện tích đất của Việt Nam khoảng 310070 km2 thuộc khoảng
Trong bốn lần cân một lượng hóa chất làm thí nghiệm ta thu được các kết quả sau đây với độ chính xác 0,001 g
5,382 g ; 5,384 g ; 5,385 g ; 5,386 g
Sai số tuyệt đối và số chữ số chắc chắn đúng của kết quả là
Với những giá trị nào sau đây của biến n∈N, mệnh đề chứa biến P(n): "n chia hết cho 12" đúng?
Cho các tập hợp:
A={1;2;3;4}; B={2;4;6;8};
C={6;5;4;3}.
Nối các phép toán với kết quả thích hợp.
Tập hợp E=(7;+∞)\(−∞;−5] bằng tập hợp nào sau đây?
Bấm chọn phần nửa mặt phẳng không phải là miền nghiệm của bất phương trình 3x+y≥1.
Điểm A(−1;3) thuộc miền nghiệm của bất phương trình nào sau đây?
Cho hệ bất phương trình {x+y−2≤02x−3y+2>0. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình?
Miền nghiệm của hệ bất phương trình ⎩⎨⎧x+y−1≥0y≥2−x+2y≥3 là phần không tô màu của hình vẽ nào sau đây?
Mệnh đề nào sau đây đúng?
Xét tính đúng, sai của các mệnh đề sau:
(Nhấp vào dòng để chọn đúng / sai)| C: "Hai đường chéo của một tứ giác bằng nhau là điều kiện cần để tứ giác đó là hình chữ nhật." |
|
| D: "Hai đường chéo của một tứ giác bằng nhau là điều kiện đủ để tứ giác đó là hình chữ nhật." |
|
| B: "Hai đường chéo của một tứ giác vuông góc với nhau là điều kiện đủ để tứ giác đó là hình thoi." |
|
| A: "Hai đường chéo của một tứ giác vuông góc với nhau là điều kiện cần để tứ giác đó là hình thoi." |
|
Một lớp có 45 học sinh. Mỗi em đều đăng kí chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng kí môn bóng đá, 15 em đăng ký môn bóng chuyền. Có bao nhiêu bạn đăng kí chơi cả hai môn?
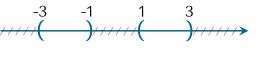
Cho tập hợp X={x∈R∣∣1≤∣x∣≤3} thì X được biểu diễn bởi hình



Cho các tập hợp A=(−2;10); B=(m;m+2). Giá trị của m để A∩B=(m;m+2) là
Biểu thức F(x;y)=y−x đạt giá trị nhỏ nhất với điều kiện ⎩⎨⎧2x−y≥2x−2y≤2x+y≤5x≥0 tại điểm có toạ độ là
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.
● Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;
● Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Vậy cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Miền nghiệm của bất phương trình 2x−2y+2−2≤0 chứa điểm nào sau đây?
Cho ba tập hợp CRM=(−∞;3); CRN=(−∞;−3)∪(3;+∞) và CRP=(−2;3]. Khẳng định nào sau đây đúng?
Cho tập hợp A=(0;+∞) và B={x∈R∣∣mx2−4x+m−3=0}. Giá trị của m để B có đúng hai tập con và B⊂A là
Một xưởng cơ khí có hai công nhân lành nghề là Nam và Định. Xưởng sản xuất hai loại sản phẩm có mã số I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Nam phải làm việc trong 3 giờ, Định phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Nam phải làm việc trong 2 giờ, Định phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Nam không thể làm việc quá 180 giờ và Định không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200 kg nguyên liệu và một máy chuyên dụng. Để sản xuất được một ki-lô-gam sản phẩm loại I cần 2 kg nguyên liệu và máy làm việc trong 3 giờ. Để sản xuất được một kilôgam sản phẩm loại II cần 4 kg nguyên liệu và máy làm việc trong 1,5 giờ. Biết một ki-lô-gam sản phẩm loại I lãi 300 000 đồng, một ki-lô-gam sản phẩm loại II lãi 400 000 đồng và máy chuyên dụng làm việc không quá 120 giờ. Xưởng cần sản xuất bao nhiêu ki-lô-gam sản phẩm mỗi loại để tiền lãi lớn nhất?
Giá trị nhỏ nhất của biết thức F=y−x trên miền xác định bởi hệ ⎩⎨⎧2x+y≤2x−y≤25x+y≥−4 là
Số tập con của tập hợp A={x∈R∣∣3(x2+x)2−2x2−2x=0} là
Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người, kết quả như sau:
+ Một người mỗi ngày có thể tiếp nhận được không quá 600 đơn vị vitamin A và không quá 500 đơn vịvitamin B.
+ Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A lẫn B.
+ Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn 12 số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A. Giá của 1 đơn vị vitamin A là 9 đồng, giá 1 đơn vị vitamin B là 7,5 đồng.
Tìm phương án dùng hai loại vitamin A và B thỏa mãn các điều kiện trên, trong đó số tiền phải trả mỗi ngày là ít nhất?
