Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Qua bài học này, người học sẽ nắm được:
- Khái niệm đa thức một biến.
- Cách sắp xếp và thu gọn đa thức một biến.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Chọn ra các hạng tử của đa thức C=3x5−2x2−x5+1.
Chú ý dấu của từng hạng tử.
3x5.
−x5.
−2x2.
2x2.
x5.
1.
Câu 2 (1đ):
Chọn các hạng tử của đa thức A=6x3−5x4−3x3+2x2+2.
2x2.
−3x3.
6x3.
2.
3x3.
5x4.
−5x4.
Câu 3 (1đ):
Chọn hai hạng tử cùng bậc của đa thức A=6x3−5x4−3x3+2x2+2.
−5x4.
2x2.
6x3.
2.
−3x3.
Câu 4 (1đ):
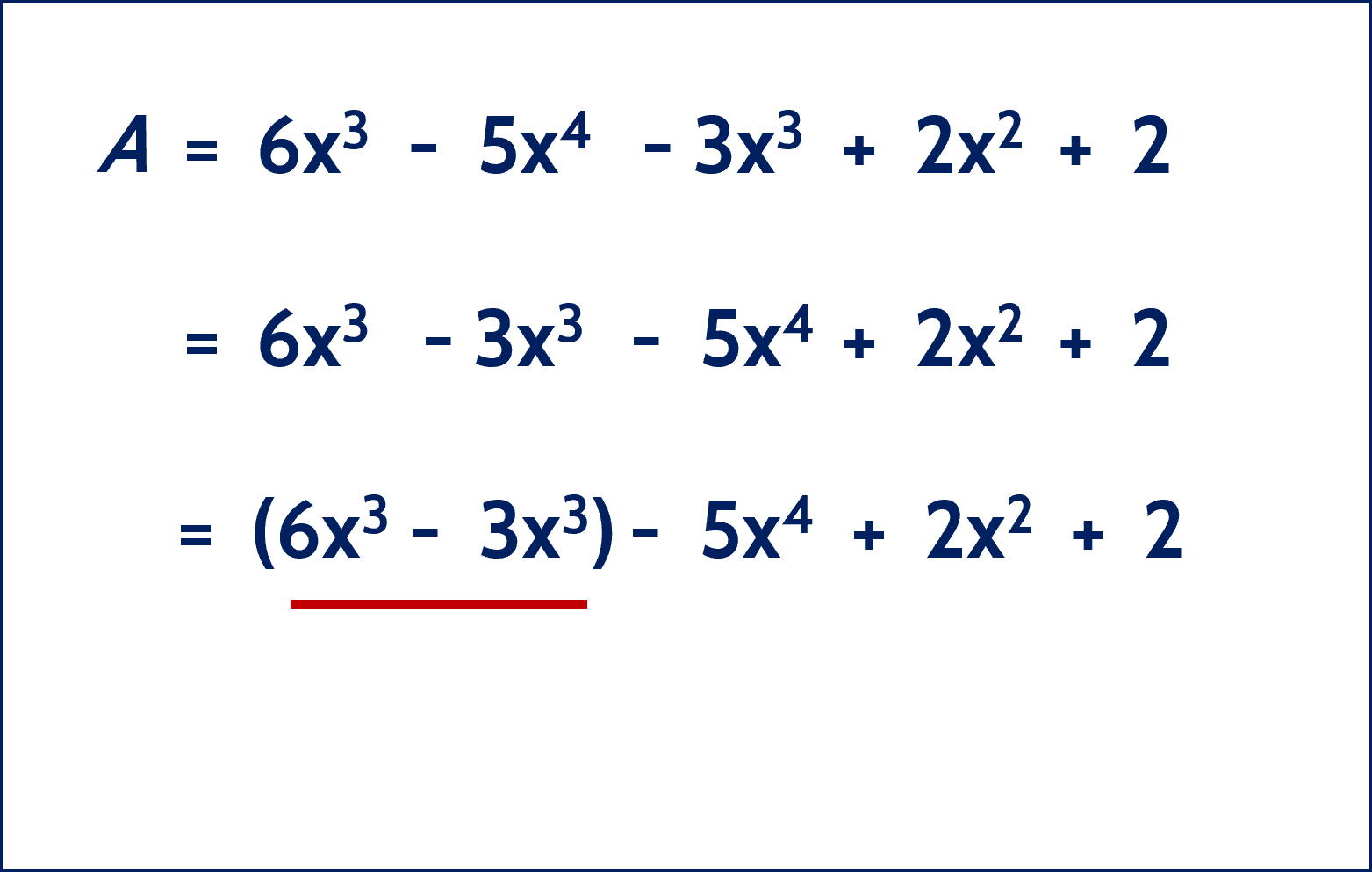
Cộng hai đơn thức trong ngoặc, ta được
A
A=−3x3−5x4+2x2+2.
B
A=3x3−5x4+2x2+2.
C
A=9x3−5x4+2x2+2.
Câu 5 (1đ):
Cho đa thức A=3x3−5x4+2x2+2. Phân loại hạng tử của đa thức A vào các bậc của lũy thừa biến x tương ứng.
- 2
- 3x3
- −5x4
- 2x2
Bậc 4
Bậc 3
Bậc 2
Bậc 1
Bậc 0
Câu 6 (1đ):
Đa thức A=3x−4x4+x3 có cần phải thu gọn không?
Có.
Không.
Câu 7 (1đ):
Sắp xếp đa thức theo lũy thừa giảm dần của biến
A=
- +3x
- −4x4
- +x3
Câu 8 (1đ):
Cho đa thức B=x5−21x3+43x−x5+6x2−2.
Chọn ra hai đơn thức cùng bậc trong đa thức trên.
−x5.
6x2.
−2.
x5.
43x.
−21x3.
Câu 9 (1đ):
Thu gọn và sắp xếp B=x5−21x3+43x−x5+6x2−2 theo lũy thừa giảm dần của biến, ta được
(1) B=2x5−21x3+6x2+43x−2.
(2) B=−21x3+6x2+43x−2.
(3) B=43x−21x3+6x2−2.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- sang máy bay học lần này thì chúng ta sẽ
- cùng nhau tìm hiểu về đa thức một biến
- chúng ta đi vào phần đầu tiên khái niệm
- đa thức một biến
- đã thức một biến hay còn gọi tắt là đa
- thức là tổng của những đơn thức của cùng
- một biến
- và trong phần này thì chúng ta chủ yếu
- sẽ nghiên cứu các đa thức có cùng biến x
- trên màn hình là ví dụ của đa thức một
- biến là thư một biến a bằng 6x^3 - 5x² -
- 4x^3 + 7
- nếu như chúng ta soi vào định nghĩa thì
- đa thức một biến là tổng của những đơn
- thức Tuy nhiên ở đây chúng ta lại thấy
- xuất hiện phép trừ
- vậy Tại sao biểu thức A vẫn được gọi là
- đa thức một biến
- nhưng chúng ta đã biết ở trong biểu thức
- số thì phép trừ có thể coi là phép cộng
- với số đối và điều này cũng đúng với các
- biểu thức chứa biến chúng ta có thể viết
- lại đa thức A như sau
- thức a = 6x³
- từ 5x bình phương Chúng ta sẽ viết là
- cộng với âm 5x² như thế này tiếp theo là
- cộng với -4x^3 và cuối cùng là cộng 7
- như vậy là chúng ta đã thấy đa thức một
- biến a chính là tổng của những đơn thức
- một biến x
- chúng ta rút ra một số nhận xét về đa
- thức một biến đầu tiên là về tên của đa
- thức một biến tên của đa thức được ký
- hiệu là chữ in hoa như là A B Q R
- Ngoài ra thì chúng ta có thể bắt gặp
- cách viết đa thức A như sau đó là a với
- x ở bên trong như thế này khi viết đa
- thức ax thì chúng ta hiểu đây là đa thức
- với một biến cụ thể là biến x
- đối với các đơn thức mà cấu tạo nên đa
- thức A thì chúng ta sẽ gọi đây là các
- hạng tử
- cụ thể hơn thì đa thức a sẽ có các hạng
- tử là 6x³
- - 5x mũ 2 trừ 4 x mũ 3 và Dương 7
- như vậy là chúng ta có thêm một khái
- niệm đó là hãm tử của đa thức
- mỗi đơn thức trong tổng được gọi là hạng
- tử của đa thức đó
- về việc xét Hàm Tử thì nhiều khi chúng
- ta không cần phải viết chi tiết tức là
- chuyển phép trừ thành phép cộng giống
- như thế này mà chúng ta có thể xác định
- như sau khi liệt kê mỗi hạng tử của đa
- thức A thì chúng ta cần phải mang theo
- dấu của hạng tử cụ thể hơn là dấu nằm ở
- đằng trước của hạng tử đó
- hạn tử đầu tiên là 6x³
- hạng tử số 2 là âm 5x bình phương
- mang theo dấu ở đằng trước Hạ Tử thứ ba
- là trừ 4x^3 có dấu ở đằng trước và hạng
- tử cuối cùng là dương vật
- và đây cũng chính là cách chúng ta liệt
- kê hạng tử của đa thức a
- Chúng Ta Đi Vào phần luyện tập sau đây
- Liệt kê các hạng tử của đa thức C
- 3x^5 - 2x bình trừ 5x + 1
- chúng ta sẽ hình dung đa thức C là tổng
- của các hạng tử như sau
- như vậy hạng tử của đa thức C bao gồm
- 3x^5
- -2x^2 nếu mang theo dấu
- tiếp theo là trừ x mũ 5 và cuối cùng là
- 1
- như vậy là ở trong phần này thì chúng ta
- đã hiểu như thế nào là một đa thức một
- biến và hạng tử của đa thức một biến
- sang cái phần tiếp theo chúng ta sẽ cùng
- nhau sắp xếp và thu gọn đa thức một biến
- khi chúng ta tìm hiểu về một đa thức một
- biến thì chắc chắn chúng ta sẽ phải
- nghiên cứu các phép toán cộng trừ nhân
- chia đa thức một biến thế nên việc sắp
- xếp và thu gọn đa thức một biến sẽ khiến
- chúng ta có thể tính toán dễ dàng và
- chính xác hơn
- Phần đầu tiên là chúng ta sẽ thu gọn đa
- thức một biến
- thầy có các thức A như sau
- đầu tiên chúng ta có thể nhận xét thấy
- đa thức a có 2 đơn thức cùng bậc nên
- chúng ta hoàn toàn có thể nghĩ đến việc
- cộng hai đơn thức cùng bậc ở trong bài
- trước chúng ta nhà khoa học và Như vậy
- chúng ta sẽ thu gọn đa thức một biến khi
- chúng ta thấy xuất hiện các đơn thức
- cùng bậc cụ thể hơn hai đơn thức cùng
- bậc là 6x^3 và trừ 3x^3 nhớ mang theo
- dấu của đơn thức
- bây giờ chúng ta sẽ sử dụng tính chất
- giao hoán và kết hợp của phép cộng để
- tính toán các đơn thức cùng Bậc
- và chúng ta cũng cần phải chú ý dấu của
- hạng tử khi áp dụng tính chất Giao hoán
- và kết hợp
- ta sẽ giao thoa nó kết hợp đưa hai đơn
- thức 6x^3 và trừ 3x^3 về lại gần nhau
- Sau đó chúng ta sử dụng tính chất kết
- hợp
- đến đây thì cộng trừ hai đơn thức cùng
- bậc chúng ta được kết quả là 3x^3 trừ đi
- 5x^4 + 2x^2 + 2
- sau khi thu gọn thì chúng ta lại kiểm
- tra và ta thấy đa thức a sau khi thu gọn
- không còn hai hạng tử nào cùng bậc
- như vậy là chúng ta sẽ dùng hành động
- thu gọn đa thức một biến
- sau khi thu gọn thì chúng ta sẽ sắp xếp
- đa thức một biến
- và cụ thể hơn là chúng ta sẽ sắp xếp các
- hạng tử của đa thức theo lũy thừa giảm
- dần của biến
- hạ từ cao nhất là hạng tử bậc 4 trừ 5x
- mũ 4
- vẫn mang theo dấu của hạng tử này
- tiếp theo là đến 3x^3 tức là cộng 3x^3
- rồi 2x^2 và cộng 2
- như vậy là chúng ta đã sắp xếp hạng tử
- theo lũy thừa giảm dần của biến cụ thể
- hơn là từ bậc 4 đến bậc 3 bậc 2 rồi đến
- bằng 0
- ở Đa thức này chúng ta không thấy hạng
- tử bậc nhất về sau nhiều khi để tiện cho
- tính toán thì chúng ta hoàn toàn có thể
- thêm đơn thức bậc nhất là cộng 0x như
- thế này để tiện cho việc tính toán
- như vậy là chúng ta đã hiểu cách sắp xếp
- và thu gọn đa thức một biến bây giờ
- chúng ta sẽ đến với một số bài tập
- Ôn tập lại thu gọn nếu cần và sắp xếp
- mỗi đa thức sau theo lũy thừa giảm dần
- của biến
- thầy có 2 phần đa thức a và đa thức B
- chúng ta sẽ làm câu a trước ở Đa thức A
- thì chúng ta thấy Không thấy xuất hiện
- hai hạng tử nào cùng bậc do đó đa thức a
- là một đa thức đã thu gọn
- và đến đây Chúng ta chỉ cần sắp xếp đa
- thức theo lũy thừa giảm dần của biến cụ
- thể chúng ta sắp xếp như sau hạng tử có
- bậc lớn nhất là hạng tử -4x^4
- sau đó đến hạn tử bậc 3 là x mũ 3 và
- cuối cùng là hạng tử 3x
- sang đến câu b
- ở câu b ta thấy xuất hiện hai hạng tử
- cùng bậc là x mũ 5 và trừ x mũ 5
- nên chúng ta sẽ sử dụng tính chất Giao
- hoán và kết hợp để gói x^5 và trừ x mũ 5
- ta sử dụng tính chất Giao hoán như sau
- khi giao hoán nếu mang dấu của hạng tử
- sau đó sử dụng tính chất kết hợp và tính
- toán như bình thường thì chúng ta đã mất
- đi hạng tử bậc 5
- và đến đây thì sắp xếp đa thức theo lũy
- thừa giảm dần của biến thì chúng ta được
- các hạng tử được sắp xếp từ bậc 3 tới
- bậc 2 bậc 1 xuống tới bậc 0
- ở đây cũng là bài tập cuối cùng thầy
- mang đến cho các em ở trong phần này
- trên màn hình của chúng ta là một số nội
- dung cần nhớ về đa thức một biến
- [âm nhạc]
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây