Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
(1,5 điểm) Tính giá trị của biểu thức.
a) $\dfrac{7}{2}-\left(\dfrac{3}{4}+\dfrac{1}{5}\right)$
b) $\dfrac{12}{23} . \dfrac{7}{13}+\dfrac{11}{23} . \dfrac{7}{13};$
c) $|-2|-\left(\dfrac{5}{9}-\dfrac{2}{3}\right)^2: \dfrac{4}{27}.$
Hướng dẫn giải:
a) $\dfrac{7}{2}-\left(\dfrac{3}{4}+\dfrac{1}{5}\right)$
$=\dfrac{7}{2}-\left(\dfrac{15}{20}+\dfrac{4}{20}\right)$
$=\dfrac{7}{2}-\dfrac{19}{20}$
$=\dfrac{70}{20}-\dfrac{19}{20}$
$=\dfrac{51}{20}$
b) $\dfrac{12}{23} . \dfrac{7}{13}+\dfrac{11}{23} . \dfrac{7}{13}$
$ =\dfrac{7}{13} .\left(\dfrac{12}{23}+\dfrac{11}{23}\right) $
$=\dfrac{7}{13} . 1$
$=\dfrac{7}{13}$
c) $|-2|-\left(\dfrac{5}{9}-\dfrac{2}{3}\right)^2: \dfrac{4}{27}.$
$=2-\left( \dfrac{-1}{9} \right)^2 : \dfrac{4}{27}$
$=2-\dfrac{1}{81}:\dfrac{4}{27}$
$=2-\dfrac{1}{81} \cdot \dfrac{27}{4}$
$=2-\dfrac{1}{81} \cdot \dfrac{27}{4}$
$=2-\dfrac{1}{12}$
$=\dfrac{23}{12}$
(1,5 điểm) Tìm $x$ biết
a) $\dfrac{3}{4}-\left(x-\dfrac{2}{3}\right)=1 \dfrac{1}{3}$;
b) $\Big| \dfrac{1}{3}-x \Big|=\dfrac{2}{5}$;
c) $\dfrac{x-1}{3}=\dfrac{27}{x-1}$.
Hướng dẫn giải:
a) $\dfrac{3}{4}-\left(x-\dfrac{2}{3}\right)=1 \dfrac{1}{3}$
$\left(x-\dfrac{2}{3}\right) =\dfrac{3}{4} - \dfrac{4}{3} $
$x-\dfrac{2}{3}= \dfrac{-7}{12} $
$x= \dfrac{-7}{12} + \dfrac{2}{3}$
$x= \dfrac{1}{12}$
b) $\Big| \dfrac{1}{3}-x \Big|=\dfrac{2}{5}$;
$\dfrac{1}{3}-x =-\dfrac{2}{5}$ hoặc $\dfrac{1}{3}-x =\dfrac{2}{5}$
$x =\dfrac{11}{15}$ hoặc $x =\dfrac{-1}{15}$
c) $\dfrac{x-1}{3}=\dfrac{27}{x-1}$.
Áp dụng tính chất tỉ lệ thức, ta được:
$(x-1)^2=3.27$
$(x-1)^2=81$
$x-1=9$ hoặc $x-1=-9$
$x=10$ hoặc $x=-8$
(1,5 điểm) Để hưởng ứng phong trào quyên góp sách, ba lớp $7A,\,7B,\,7 {C}$ đã quyên góp được tổng số $180$ cuốn sách. Biết số cuốn sách của 3 lớp $7 A,\, 7 B,\, 7 C$ tỉ lệ với các số $5 ; 6 ; 4$. Tính số sách mà mỗi lớp đã quyên góp được.
Hướng dẫn giải:
Gọi số sách mà ba lớp $7 A, 7 B, 7 C$ quyên góp được lần lượt là $x ; y ; z$ $\left(x ; y ; z \in \mathbb{N}^* ; x, y, z \leq 180\right)$
Vì số cuốn sách của 3 lớp $7 A, 7 B, 7 C$ tỉ lệ với các số $5 ; 6 ; 4$ ta có: $\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{4}$.
Vì đã quyên góp được tổng số $180$ cuốn sách nên : $x+y+z=180$
Ta có: $\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{4}=\dfrac{x+y+z}{5+6+4}=\dfrac{180}{15}=12$.
Khi đó ta có:
$\dfrac{x}{5}=12 \Rightarrow x=12.5 \Rightarrow x=60({TM})$
$\dfrac{y}{6}=12 \Rightarrow y=12.6 \Rightarrow y=72({TM})$
$\dfrac{z}{4}=12 \Rightarrow z=12.4 \Rightarrow z=48({TM})$
Vậy số sách mà ba lớp $7 A, 7 B, 7 C$ quyên góp được lần lượt là $60;72;48$ cuốn sách.
(2 điểm) Cho hình vẽ, biết $m$ $//$ $n$; $AB \bot m;$ $\widehat{ACF}=120^{\circ}$; $\widehat{ADE}=50^{\circ}$;
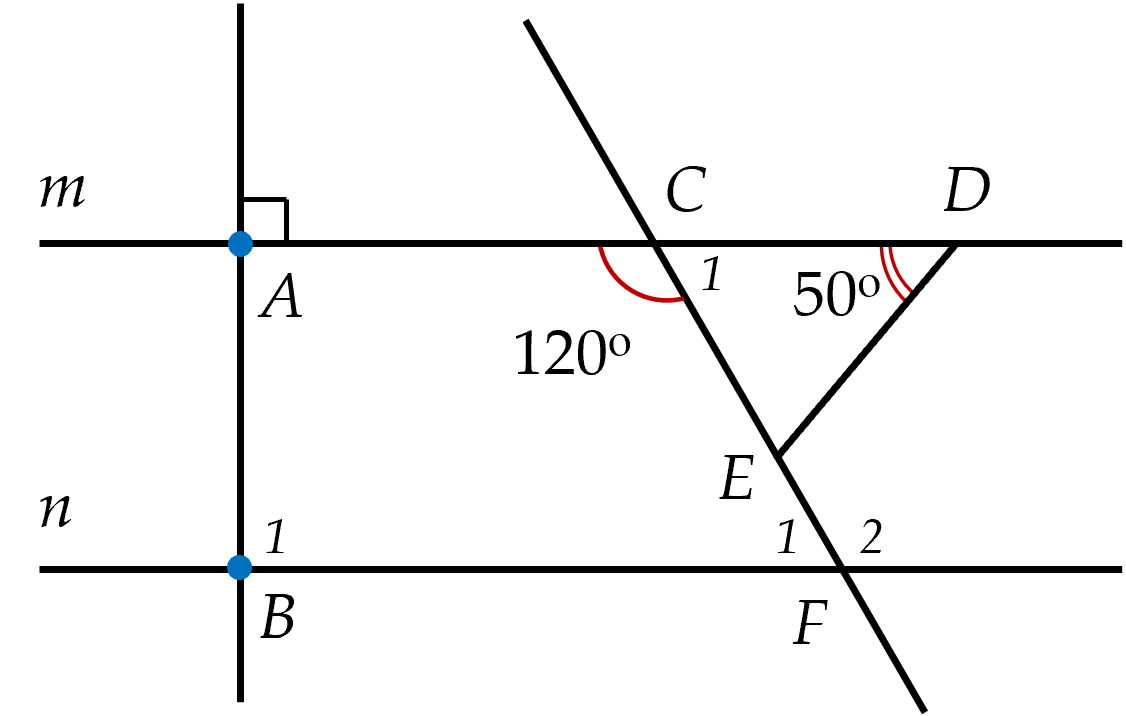
a) Vẽ lại hình vào bài thi.
b) Tình số đo góc $C_1$ và góc $F_1$.
c) Chứng minh đường thẳng $AB$ vuông góc với đường thẳng $n$.
d) Tính số đo của góc $DEF$.
Hướng dẫn giải:
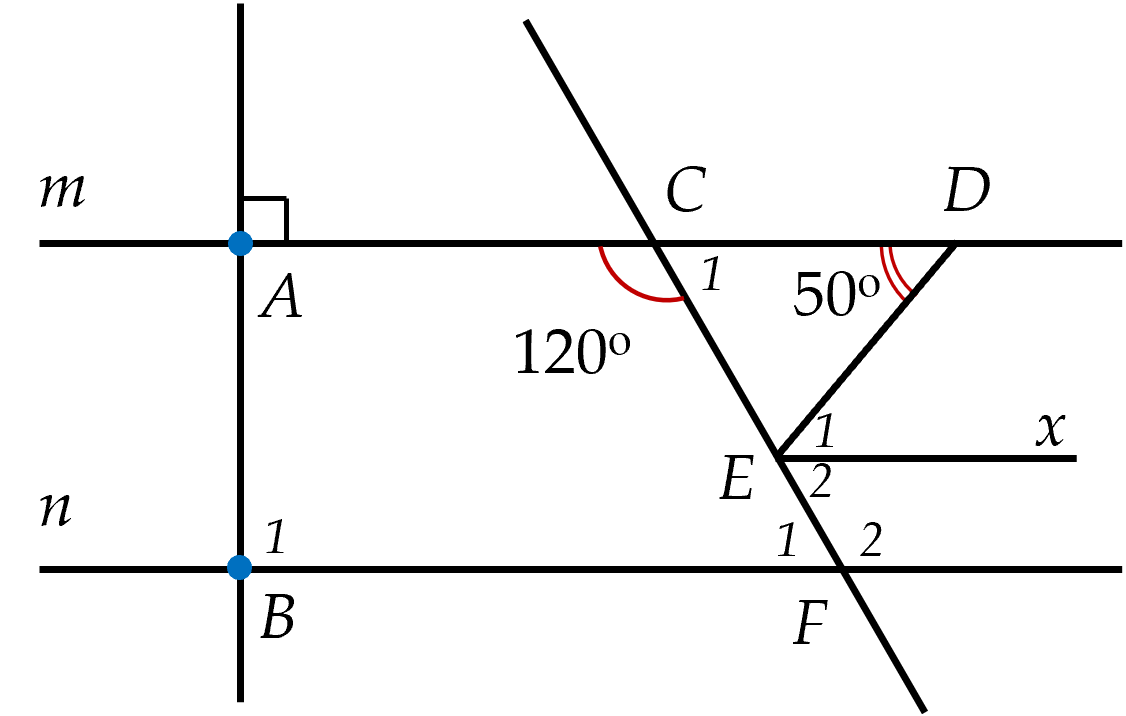
a) Học sinh tự vẽ hình vào bài làm.
b)Ta có: góc $ACF$ kề bù với góc $C_1$
$\Rightarrow \widehat{ACF} + \widehat{C_1}=180^{\circ}$
Thay số tính được góc $C_1=60^{\circ}$
Ta có $m$$//$$n$
Suy ra $\widehat{C_1}=\widehat{F_1}$ (2 góc so le trong)
$\Rightarrow \widehat{F_1}=60^{\circ}$
c) Từ $m / / n$, suy ra $\widehat{A_1} = \widehat{B_1}=90^{\circ}$ (hai góc đồng vị).
Vậy $AB \bot n$.
d) Kẻ $E x / / m$. Ta có $m / / n$ (gt). Suy ra $E x / / m / / n$
Xét $E x / / m$ có:
$\widehat{A D E}=\widehat{E_1}=50^{\circ}$ (hai góc so le trong)
Xét $E x$ $//$ $n$ có:
$\widehat{E_2}=\widehat{F_1}=60^{\circ}$ ( 2 góc so le trong)
Vậy $\widehat{D EF}=\widehat{E_1}+\widehat{E_2}=50^{\circ}+60^{\circ}=110^{\circ}$
(0,5 điểm) Cho $\dfrac{a}{c}=\dfrac{c}{b}.$ Chứng minh $\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a}{b}$.
Hướng dẫn giải:
Đặt $\dfrac{a}{c}=\dfrac{c}{b}=k(k \neq 0)$ suy ra:
$c=b . k $
$a=c.k=b . k . k=b . k^2$
Ta có:
$\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{\left(b . k^2\right)^2+(b . k)^2}{b^2+(b . k)^2}=\dfrac{b^2 k^4+b^2 k^2}{b^2+b^2 k^2}=\dfrac{b^2 k^2\left(k^2+1\right)}{b^2\left(1+k^2\right)}=k^2$
$\dfrac{a}{b}=\dfrac{b . k^2}{b}=k^2$
Do đó: $\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a}{b}$.
