Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Theo báo cáo của Tổng cục hải quan, số lượng và giá trị nhập khẩu phân bón các loại của nước ta trong các năm 2017, 2018, 2019, 2020 được thống kê ở bảng sau:
| Năm | 2017 | 2018 | 2019 | 2020 |
| Số lượng nhập khẩu (nghìn tấn) |
$4 727,3$ | $4 227,5$ | $3 799,2$ | $3 803,4$ |
| Giá trị nhập khẩu (triệu đô la Mỹ) |
$1 253,1$ | $1 202,8$ | $1 047,7$ | $951,5$ |
a) Tính tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020 .
b) Số lượng nhập khẩu phân bón các loại năm 2019 giảm bao nhiêu phần trăm so với năm 2018 (làm tròn kết quả đến hàng phần mười)?
c) Giá trị nhập khẩu phân bón các loại năm 2017 gấp bao nhiêu lần giá trị nhập khẩu phân bón các loại năm 2020 (làm tròn kết quả đến hàng phần mười)?
Hướng dẫn giải:
a) Tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020 là:
$4\,727,3 + 4\,227,5 + 3\,799,2 + 3\,803,4 = 16\,557,4$ (nghìn tấn)
b) Số % nhập khẩu phân bón các loại năm 2019 giảm so với năm 2018 là:
$\dfrac{(4\,227,5-3\,799,2) . 100 \%}{4\,227,5}=\dfrac{428,3 . 100 \%}{4\,227,5} \approx 10,1 \%$
c) Giá trị nhập khẩu phân bón các loại năm 2017 gấp giá trị nhập khẩu phân bón các loại năm 2020 số lần là:
$\dfrac{1\,253,1}{951,5} \approx 1,3$ (lần)
Tìm nghiệm của đa thức $P(x)=5x+3$.
Hướng dẫn giải:
Nghiệm của đa thức $P(x)=5x+3$ là $x=\dfrac{-3}{5}$.
Cho tam giác $ {ABC}$ cân tại $ {A}$ có $\hat{A}<90^{\circ}$. Vẽ $ {BD}$ vuông góc với $ {AC}$ tại $ {D}, {CE}$ vuông góc với $ {AB}$ tại $ {E}$.
a) Chứng minh: $ {AD}= {AE}$.
b) Gọi $ {I}$ là giao điểm của $ {BD}$ và $ {CE}$. Chứng minh : $ {AI}$ là tia phân giác của góc $ {BAC}$.
c) Chứng minh : $ {DE} / / {BC}$.
Hướng dẫn giải:
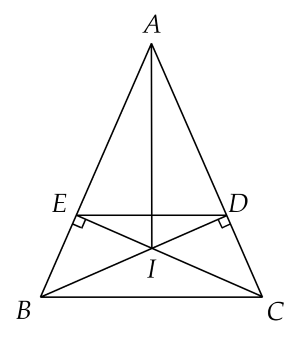
a) Xét $\Delta DAB$ và $\Delta EAC$ lần lượt vuông tại $D$ và $E$ có:
$AB=AC$ ($\Delta ABC$ cân tại $A$);
$\widehat{BAC}$ chung.
Suy ra $\Delta DAB = \Delta EAC$ (cạnh huyền, góc nhọn)
Suy ra $AD = AE$ (hai cạnh tương ứng).
b) Xét $\Delta EAI$ và $\Delta DAI$ lần lượt vuông tại $E$ và $D$:
$AE = AD$
Chung cạnh $AI.$
Suy ra $\Delta EAI = \Delta DAI$ (cạnh huyền, cạnh góc vuông).
Suy ra $ \widehat{E A I}=\widehat{D A I}$ (hai góc tương ứng).
Suy ra $AI$ là tia phân giác của $\widehat{BAC}$.
c) Có $AD=AE$ suy ra $\Delta AED$ cân tại $A$.
Suy ra $\widehat{AED} = \dfrac{180^{\circ}-\widehat{BAC}}{2}$
Tam giác $ABC$ cân tại $A$, suy ra $\widehat{ABC} = \dfrac{180^{\circ}-\widehat{BAC}}{2}$.
Từ $(1)$ và $(2)$ suy ra $\widehat{AED} = \widehat{ABC}$ (hai góc ở vị trí đồng vị) nên $ED$ // $BC$.
Ba địa điểm $ {A}, {B}, {C}$ là 3 đỉnh của tam giác $ {ABC}$ với $\widehat{A}=90^{\circ}$ và khoảng cách giữa 2 địa điểm $ {A}$ và $ {C}$ là $550$ m. Người ta đặt một loa truyền thanh tại một địa điểm nằm giữa $ {A}$ và $ {B}$ thì tại $ {C}$ có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là $550$ m?
Hướng dẫn giải:
Ta có hình vẽ:
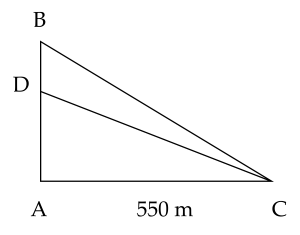
Gọi vị trí đặt loa là $D$ suy ra $D$ nằm giữa $A$ và $B$.Trong tam giác vuông $ADC$ ta có $DC$ là cạnh lớn nhất (đối diện với góc lớn nhất) nên $DC > AC = 550$ m. Vậy tại $C$ không thể nghe tiếng loa, do vị trí $C$ đã nằm ngoài bán kính phát sóng của loa.
