Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: sự đồng quy của ba đường phân giác của tam giác SVIP
Cho $\triangle A B C$ có $A B<A C$. Tia phân giác của $\widehat{A}$ cắt đường thẳng vuông góc với $B C$ tại trung điểm của $B C$ ở $D$. Gọi $H$ và $K$ là chân các đường vuông góc kẻ từ $D$ đến các đường thẳng $A B$, $A C$. Chứng minh $B H=C K$.
Hướng dẫn giải:
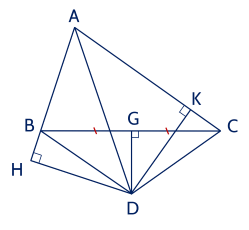
Ta có $D$ thuộc phân giác của $\widehat{A}$;
$D H \perp A B$; $D K \perp A C$ $\Rightarrow D H=D K$ (tính chất tia phân giác của một góc).
Gọi $G$ là trung điểm của $BC$.
Xét $\triangle B G D$ và $\triangle C G D$, có
$\widehat{B G D}=\widehat{C G D}=90^{\circ}$ ($DG$ là trung trực của $B C$ ),
$BG=CG$ (già thiết),
$DG$ là cạnh chung.
Do đó $\triangle B G D=\triangle C G D$ (hai cạnh góc vuông)
$\Rightarrow B D=C D$ (hai cạnh tương ứng).
Xét $\triangle B H D$ và $\triangle C K D$, có
$\widehat{B H D}=\widehat{C K D}=90^{\circ}$ (giả thiết);
$D H=D K$ (chứng minh trên);
$B D=C D$ (chứng minh trên).
Do đó $\triangle B H D=\triangle C K D$ (cạnh huyền - cạnh góc vuông)
$\Rightarrow B H=C K$ (hai cạnh tương ứng).
Cho $\triangle ABC$ có $\widehat{A}=120^{\circ}$. Tia phân giác của $\widehat{A}$ cắt $BC$ tại $D$. Tia phân giác của $\widehat{ADC}$ cắt $AC$ tại $I$. Gọi $H$, $K$ lần lượt là hình chiếu của $I$ trên đường thẳng $AB$, $BC$. Chứng minh $IH=IK$.
Hướng dẫn giải:
Kẻ $IE \perp AD$ (với $E \in A D$).
Gọi $A x$ là tia đối của tia $A B$.
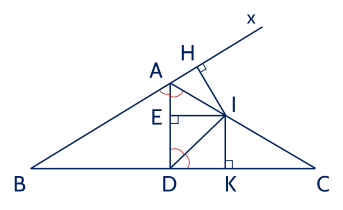
Vì $\widehat{B A C}$ và $\widehat{C A x}$ là hai góc kề bù mà $\widehat{B A C}=120^{\circ}$ nên $\widehat{C A x}=60^{\circ}$ (1)
Ta có $AD$ là phân giác của $\widehat{B A C} \Rightarrow \widehat{D A C}=\dfrac{1}{2} \widehat{B A C}=60^{\circ}$ (2)
Từ (1) và (2) suy ra $A C$ là tia phân giác của $\widehat{D A x}$
$\Rightarrow I H=I E$ (tính chất tia phân giác của một góc) (3)
Vì $D I$ là phân giác của $\widehat{A D C}$ nên $I K=I E$ (tính chất tia phân giác của một góc) (4)
Từ (3) và $(4)$ suy ra $I H=I K$.
Cho $\widehat{xOy}$, $\left(0^{\circ}<\widehat{x O y}<180^{\circ}\right)$, $Om$ là tia phân giác $\widehat{xOy}$. Trên tia $Om$ lấy điểm $I$ bất kì. Gọi $E, \, F$ lần lượt là chân đường vuông góc kẻ từ $I$ đến $O x$ và $O y$. Chứng minh:
a) $\triangle I O E=\triangle I O F$.
b) $E F \perp O m$.
Hướng dẫn giải:
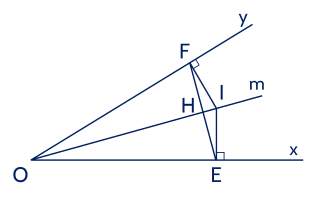
a) Xét $\triangle I O E$ và $\triangle I O F$ có
$\widehat{E}=\widehat{F}=90^{\circ}$ (giả thiết);
$O I$ cạnh chung;
$\widehat{E O I}=\widehat{F O I}$ ($Om$ là tia phân giác).
Vậy $\triangle I O E=\triangle I O F$ (cạnh huyền - góc nhọn).
b) $\triangle I O E=\triangle I O F$ (chứng minh trên)
$\Rightarrow O E=O F$ (hai cạnh tương ứng).
Gọi $H$ là giao điểm của $O m$ và $E F$.
Xét $\triangle O H E$ và $\triangle O H F$, có
$O E=O F$ (chứng minh trên);
$\widehat{E O H}=\widehat{F O H}$ ($O m$ là tia phân giác);
$\mathrm{OH}$ chung.
Do đó $\triangle O H E=\triangle O H F$ (c.g.c)
$\Rightarrow \widehat{O H E}=\widehat{F H O}$ (hai góc tương ứng)
Mà $\widehat{O H E}+\widehat{F H O}=180^{\circ}$ nên $\widehat{O H E}=\widehat{F HO}=90^{\circ}$.
Vậy $E F \perp O m$.
Cho $\widehat{xOy}$. Lấy các điểm $A, \, B$ thuộc tia $O x$ sao cho $O A>O B$. Lấy các điểm $C, \, D$ thuộc $O y$ sao cho $O C=O A, \, O D=O B$. Gọi $E$ là giao điểm của $A D$ và $B C$. Chứng minh rằng
a) $A D=B C$.
b) $\triangle A B E=\triangle C D E$.
c) $O E$ là tia phân giác của $\widehat{x O y}$.
Hướng dẫn giải:
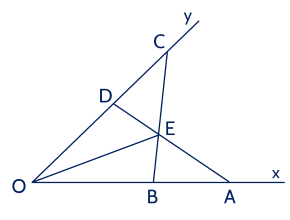
a) Xét $\triangle O A D$ và $\triangle O C B$, có
$O A=O C$ (giả thiết);
$\widehat{O}$ chung;
$O D=O B$ (giả thiết).
Do đó $\triangle O A D=\triangle O C B$ (c.g.c)
$\Rightarrow A D=C B$ (hai cạnh tương ứng).
b) Do $O A=O C$ và $O B=O D$ nên $A B=C D$.
Mà $\triangle O A D=\triangle O C B$ (chứng minh trên)
$\Rightarrow \widehat{O B C}=\widehat{O D A}$; $\widehat{O A D}=\widehat{O C B}$ (hai góc tương ứng)
Mặt khác $\widehat{A B E}+\widehat{O B C}=\widehat{C D E}+\widehat{O D A}=180^{\circ}$
$ \Rightarrow \widehat{A B E}=\widehat{CDE}$
Xét $\triangle A B E$ và $\triangle C D E$ có
$\widehat{O A D}=\widehat{O C B}$ (chứng minh trên);
$A B=C D$ (chứng minh trên);
$\widehat{A B E}=\widehat{C D E}$ (chứng minh trên)
Do đó $\triangle A B E=\triangle C D E$ (g.c.g).
c) Vi $\triangle A B E=\triangle C D E$ (chứng minh trên) nên $A E=C E$ (hai cạnh tương ứng).
Xét $\triangle A E O$ và $\triangle C E O$ có $A E=C E$ (chứng minh trên);
$O E$ cạnh chung;
$O A=O C$ (giả thiết).
Do đó $\triangle A E O=\triangle C E O$ (c.c.c)
$\Rightarrow \widehat{A O E}=\widehat{C O E}$ (hai góc tương ứng)
$\Rightarrow O E$ là tia phân giác của $\widehat{x O y}$.
Cho tam giác $A B C$ cân tại $A$. $C P, \, B Q$ là các đường phân giác trong của $\triangle A B C$ $(P \in A B, \,Q \in A C)$. Gọi $O$ là giao điểm của $C P$ và $B Q$.
a) Chứng minh tam giác $O B C$ là tam giác cân.
b) Chứng minh điểm $O$ cách đều ba cạnh $A B, \, A C$ và $B C$.
c) Chứng minh đường thẳng $A O$ đi qua trung điểm của đoạn thẳng $B C$ và vuông góc với nó.
d) Chứng minh $C P=B Q$.
e) Tam giác $A P Q$ là tam giác gì? Vì sao?
Hướng dẫn giải:
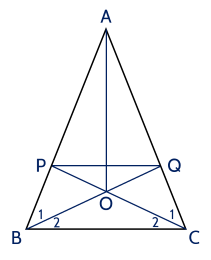
a) $\triangle A B C$ cân tại $A$ nên $\widehat{A B C}=\widehat{A C B}$.
Vì $B Q$ và $C P$ là đường phân giác của $\widehat{B}, \, \widehat{C}$ nên $\widehat{B_1}=\widehat{B_2}=\dfrac{\widehat{A B C}}{2}$, $\widehat{C_1}=\widehat{C_2}=\dfrac{\widehat{A C B}}{2}$.
Do đó $\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}$.
Suy ra $\triangle O B C$ cân tại $O$.
b) Vì $O$ là giao điểm các đường phân giác $C P$ và $B Q$ trong $\triangle A B C$ nên $O$ là giao điểm ba đường phân giác trong $\triangle A B C$.
Do đó, $O$ cách đều ba cạnh $A B, \, A C$ và $B C$.
c) Ta có $\triangle A B C$ cân tại $A, \, A O$ là đường phân giác của góc $A$ nên $A O$ đồng thời là trung tuyến và đường cao của $\triangle A B C$.
Vậy đường thẳng $A O$ đi qua trung điểm của đoạn thẳng $B C$ và vuông góc với nó.
d) Ta có $\triangle P B C=\triangle Q C B$ (g.c.g)
$\Rightarrow C P=B Q$ (hai cạnh tương ứng).
e) Ta có $A P=A B-B P$, $A Q=A C-C Q$ (1);
$\triangle P B C=\triangle Q C B \Rightarrow B P=C Q$ (2).
Lại có $A B=A C$ (tam giác $A B C$ cân tại $A$) (3).
Từ (1), (2) và (3) suy ra $A P=A Q$.
Vậy tam giác $A P Q$ cân tại $A$.
