

Lê Song Phương
Giới thiệu về bản thân



































Gọi \(ƯCLN\left(3n+2,6n+5\right)=d\) \(\left(d\inℕ^∗\right)\)
\(\Rightarrow\left\{{}\begin{matrix}3n+2⋮d\\6n+5⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}6n+4⋮d\\6n+5⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+5\right)-\left(6n+4\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(ƯCLN\left(3n+2,6n+5\right)=1\) \(\Rightarrowđpcm\)
Bạn xem lại đề bài nhé, vì thông thường phương trình hàm có 2 biến \(x,y\) chỉ có 1 phương trình thôi.
Hơn nữa nếu đề bài như thế này thì giải rất dễ. Từ pt thứ hai cho \(x=c\) với c là hằng số bất kì thì thu được \(f\left(y\right)=2y+C,\forall x,y\inℝ^+\left(C=-f\left(c\right)\right)\) là hàm số bậc nhất. Thay lại vào pt đầu tiên thì thấy vô lí.
Nên mình nghĩ đề bài có thể là
"\(f\left(x+3f\left(y\right)\right)=f\left(x\right)+f\left(y\right)\pm2y,\forall x,y\inℝ^+\)
a) Ta có \(M\left(1,m\right)\) và \(N\left(-3,n\right)\).
Vì \(M,N\in\left(P\right):y=\dfrac{1}{2}x^2\) nên ta suy ra \(m=\dfrac{1}{2};n=\dfrac{9}{2}\)
Gọi đường thẳng cần tìm là \(d:y=ax+b\). Vì \(d\) đi qua M và N nên ta có hệ pt sau:
\(\left\{{}\begin{matrix}\dfrac{1}{2}=a+b\\\dfrac{9}{2}=-3a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=\dfrac{3}{2}\end{matrix}\right.\).
Vậy ptđt cần tìm là \(d:y=-x+\dfrac{3}{2}\)
b) Mình chưa hiểu đề bài lắm. Thế nào là "cắt parabol tại 2 điểm đạt GTNN"?
Đặt \(f\left(x\right)=x^3+x+1\) thì \(f\left(x\right)\) liên tục trên \(ℝ\)
Ta có \(f\left(-1\right)=\left(-1\right)^3-1+1=-1< 0\)
\(f\left(0\right)=1>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\)
Do đó tồn tại ít nhất 1 số \(c\in\left(-1;0\right)\) sao cho \(f\left(c\right)=0\). Điều này tương đương với pt \(x^3+x+1=0\) có ít nhất 1 nghiệm âm lớn hơn \(-1\).
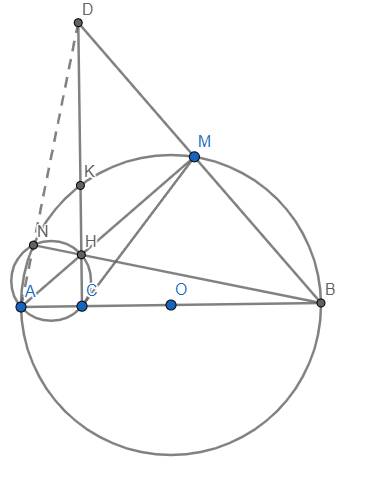
a) Xét đường tròn (O) có đường kính AB \(\Rightarrow\widehat{AMB}=90^o\)
\(\Rightarrow\widehat{AMD}=90^o\)
Lại có \(\widehat{ACD}=90^o\) nên tứ giác ACMD nội tiếp đường tròn (AD).
b) Tứ giác ACMD nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CDM}\) hay \(\widehat{CAH}=\widehat{DCB}\)
Từ đó dễ dàng chứng minh \(\Delta CAH~\Delta CDB\left(g.g\right)\)
\(\Rightarrow\dfrac{CA}{CD}=\dfrac{CH}{CB}\) \(\Rightarrow CA.CB=CH.CD\)
c) Ta thấy \(\widehat{ANH}=\widehat{ACH}=90^o\) nên tứ giác ANHC nội tiếp.
Đồng thời \(\widehat{HMB}=\widehat{HCB}=90^o\) nên tứ giác HCBM nội tiếp.
\(\Rightarrow\widehat{HCM}=\widehat{HBM}\).
Từ đó dễ dàng suy ra \(\Delta DMC~\Delta DHB\left(g.g\right)\)
\(\Rightarrow\dfrac{DM}{DH}=\dfrac{DC}{DB}\)
\(\Rightarrow DM.DB=DH.DC\)
\(\Rightarrow P_{D/\left(ANHC\right)}=P_{D/\left(O\right)}\)
\(\Rightarrow\) D thuộc trục đẳng phương của (ANHC) và (O)
\(\Rightarrow A,N,D\) thẳng hàng.
Trước tiên ta có một bổ đề sau:
Bổ đề: Cho 2 số \(a,b\) sao cho cả \(a,b\) đều viết được dưới dạng tổng của 4 số chính phương. Khi đó tích \(p=ab\) cũng có thể biểu diễn được thành tổng của 4 số chính phương.
\(\left(a_1^2+a_2^2+a_3^2+a_4^2\right)\left(b_1^2+b_2^2+b_3^2+b_4^2\right)\)
\(=\left(a_1b_1-a_2b_2-a_3b_3-a_4b_4\right)^2+\left(a_1b_2+a_2b_1+a_3b_4-a_4b_3\right)^2\) \(+\left(a_1b_3-a_2b_4+a_3b_1+a_4b_2\right)^2+\left(a_1b_4+a_2b_3-a_3b_2+a_4b_1\right)^2\)
Chứng minh thì bạn khai triển ra thôi.
Ta thấy \(0=0^2+0^2+0^2+0^2\)
\(1=0^2+0^2+0^2+1^2\)
\(2=0^2+0^2+1^2+1^2\)
Từ bổ đề trên, ta thấy chỉ cần chứng minh khẳng định đúng với số nguyên tố lẻ \(p\) thì coi như bài toán hoàn tất.
(Vì mọi số tự nhiên đều có thể viết được dưới dạng \(2^n.t\) với \(t\) lẻ)
Ta có số dư của \(a^2\) khi chia cho \(p\) luôn phân biệt khi cho \(a\) chạy từ \(0\) đến \(\dfrac{p-1}{2}\). Thật vậy, chọn \(a\) bất kì và đặt \(c=a^2modp\) \(\Rightarrow a\) là nghiệm của đa thức \(x^2-c\) trên trường \(Z/pZ\). Tương tự với \(p-a\left(\ne a\right)\). Ta biết rằng trong một trường \(K\), bất kì đa thức bậc \(n\) nào cũng chỉ có tối đa \(n\) nghiệm. Vì vậy không còn \(a\) nào khác là nghiệm của \(x^2-c\) nữa. Điều này có nghĩa là với mỗi số \(i\) trong tập hợp \(\left\{0,1,...,\dfrac{p-1}{2}\right\}\) thì tồn tại duy nhất \(a\) để \(a^2\equiv i\left[p\right]\)
Tương tự, khi \(b\) chạy từ tập \(\left\{0,1,...,\dfrac{p-1}{2}\right\}\) thì \(-b^2-1\) phân biệt. Áp dụng nguyên lí Dirichlet, tồn tại \(a,b\) sao cho \(a^2\equiv-b^2-1\left[p\right]\) \(\Leftrightarrow a^2+b^2+1^2+0^2=np\) với \(n\inℕ\)
Gọi \(m\) là số tự nhiên nhỏ nhất để \(mp\) là tổng của 4 số chính phương, \(x_1^2+x_2^2+x_3^2+x_4^2\). Ta chứng minh bằng phản chứng rằng \(m=1\) . Giả sử \(m\ne1\). Ta sẽ chỉ ra mâu thuẫn bằng việc chứng minh tồn tại một số tự nhiên \(r< m\) mà \(rp\) là tổng của 4 số chính phương.
Với mỗi \(x_i\) và \(y_i\) có cùng số dư khi chia cho \(m\) và nằm giữa \(\dfrac{-m+1}{2}\) và \(\dfrac{m}{2}\), ta có \(y_1^2+y_2^2+y_3^2+y_4^2=mr\), với \(0< r< m\)
Áp dụng bổ đề, ta có \(mpmr=z_1^2+z_2^2+z_3^2+z_4^2\). Vì \(x_i\equiv y_i\left[m\right]\) nên \(z_i⋮m\). Thật vậy:
\(z_1=x_1y_1+x_2y_2+x_3y_3+x_4y_4\) \(\equiv x_1^2+x_2^2+x_3^2+x_4^2\) \(\equiv mp\equiv0\left[m\right]\)
\(z_2=x_1y_2-x_2y_1+x_3y_4-x_4y_3\equiv x_1x_2-x_2x_1+x_3x_4-x_4x_3\equiv0\left[m\right]\)
Bằng cách tương tự chứng minh được \(z_3,z_4⋮m\)
Vậy với \(w_i=\dfrac{z_i}{m}\) thì \(w_1^2+w_2^2+w_3^2+w_4^2=rp\), điều này mâu thuẫn với tính nhỏ nhất của \(m\).
(Ta loại TH \(y_1=y_2=y_3=y_4=\dfrac{m}{2}\), khi đó \(r=m\); và TH \(y_1=y_2=y_3=y_4=0\), khi đó \(r=0\) vì cả 2 TH này đều cho ra \(mp=x_1^2+x_2^2+x_3^2+x_4^2⋮m^2\), vô lí vì \(p\) là số nguyên tố lớn hơn \(m\))
Do vậy điều giả sử là sai \(\Rightarrow\) đpcm.
Ta thấy
\(VT=\dfrac{x^2}{x^2+2xy}+\dfrac{y^2}{y^2+2yz}+\dfrac{z^2}{z^2+2zx}\)
\(\ge\dfrac{\left(x+y+z\right)^2}{x^2+2xy+y^2+2yz+z^2+2zx}\)
(áp dụng BĐT \(\dfrac{a^2}{m}+\dfrac{b^2}{n}+\dfrac{c^2}{p}\ge\dfrac{\left(a+b+c\right)^2}{m+n+p}\) với \(a,b,c,m,n,p>0\))
\(=1\) (dùng hằng đẳng thức \(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca\))
Dấu "=" xảy ra \(\Leftrightarrow\dfrac{x}{x^2+2xy}=\dfrac{y}{y^2+2yz}=\dfrac{z}{z^2+2zx}\)
\(\Leftrightarrow\dfrac{1}{x+2y}=\dfrac{1}{y+2z}=\dfrac{1}{z+2x}\)
\(\Leftrightarrow x+2y=y+2z=z+2x\)
\(\Leftrightarrow x=y=z\)
Vậy ta có đpcm. Dấu "=" xảy ra khi \(x=y=z\)
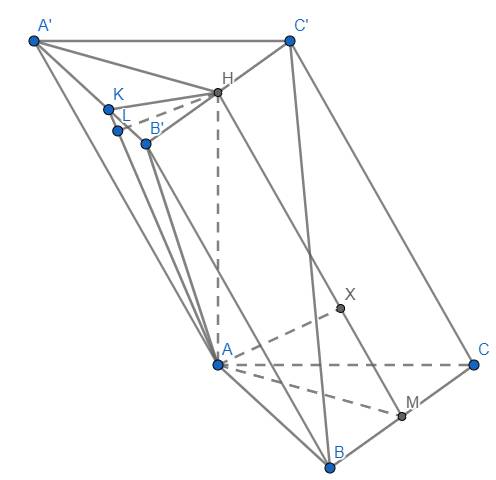
a) Có \(A'H=\dfrac{a\sqrt{3}}{2}\). Lại có \(AH\perp\left(A'B'C'\right)\) tại H nên \(\widehat{AA',\left(A'B'C'\right)}=\widehat{AA'H}=60^o\)
\(\Rightarrow AH=A'H.\tan60^o\) \(=\dfrac{a\sqrt{3}}{2}.\sqrt{3}=\dfrac{3a}{2}\)
b) Kẻ \(HK\perp A'B'\) tại K, \(HL\perp AK\) tại L.
Ta thấy \(A'B'\perp KH\) và \(A'B'\perp AH\) nên \(A'B'\perp\left(AHK\right)\)
\(\Rightarrow A'B'\perp HL\)
Mà \(HL\perp AK\) nên \(HL\perp\left(AA'B\right)\) \(\Rightarrow\left(AHK\right)\perp\left(AA'B\right)\)
Hơn nữa có \(AH\perp\left(A'B'C'\right)\) nên \(\left(AHK\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[A,A'B',C'\right]\) chính là \(\widehat{AKH}\)
Ta có \(\dfrac{1}{HK^2}=\dfrac{1}{HA'^2}+\dfrac{1}{HB'^2}\) \(=\dfrac{1}{\left(\dfrac{a\sqrt{3}}{2}\right)^2}+\dfrac{1}{\left(\dfrac{a}{2}\right)^2}\) \(=\dfrac{16}{3a^2}\)
\(\Rightarrow HK=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow\widehat{AKH}=\tan^{-1}\left(\dfrac{AH}{KH}\right)\) \(=\tan^{-1}\left(\dfrac{\dfrac{3a}{2}}{\dfrac{a\sqrt{3}}{4}}\right)\) \(=\tan^{-1}\left(2\sqrt{3}\right)\) \(\approx73,9^o\)
Vậy ...
c) Gọi M là trung điểm BC. Khi đó dễ thấy tứ giác AMHA' là hình bình hành. Kẻ \(AX\perp HM\) tại X.
Ta có \(BC\perp AM\) và \(BC\perp AH\) nên \(BC\perp\left(AMH\right)\)
\(\Rightarrow BC\perp AX\). Lại có \(AX\perp HM\) nên \(AX\perp\left(BB'C'\right)\)
\(\Rightarrow\left(AA'HM\right)\perp\left(BB'C'\right)\)
Hơn nữa vì \(AH\perp\left(A'B'C'\right)\) nên \(\left(AA'HM\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[B,B'C',A'\right]\) chính là \(\widehat{A'HM}=90^o+\widehat{AHM}=90^o+\widehat{A'AH}=90^o+30^o=120^o\)
d) \(S_đ=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V_{lt}=S_đ.h\) \(=\dfrac{a^2\sqrt{3}}{4}.\dfrac{3a}{2}\) \(=\dfrac{3a^2\sqrt{3}}{8}\) (đvtt)
Phân số này không thể là số nguyên được vì tử số là số lẻ trong khi mẫu số là số chẵn.
Theo định lý Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{3b}{2a}\\x_1x_2=\dfrac{2c}{a}\end{matrix}\right.\)
Do đó \(T=\left|x_1-x_2\right|\)
\(=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-\dfrac{3b}{2a}\right)^2-4.\dfrac{2c}{a}}\)
\(=\sqrt{\left(\dfrac{3b}{2a}\right)^2-\dfrac{8c}{a}}\)
Ta có \(a+9b+24c=0\)
\(\Leftrightarrow1+\dfrac{9b}{a}+\dfrac{24c}{a}=0\)
\(\Leftrightarrow\dfrac{24c}{a}=-\dfrac{9b}{a}-1\)
\(\Leftrightarrow\dfrac{8c}{a}=-\dfrac{3b}{a}-\dfrac{1}{3}\)
Do đó \(T=\sqrt{\left(\dfrac{3b}{2a}\right)^2+\dfrac{3b}{a}+\dfrac{1}{3}}\) \(\ge0\)
\(T=\sqrt{\left(\dfrac{3b}{2a}\right)^2+2.\dfrac{3b}{2a}+1-\dfrac{2}{3}}\)
\(T=\sqrt{\left(\dfrac{3b}{2a}+1\right)^2-\dfrac{2}{3}}\) \(\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\dfrac{3b}{2a}+1\right)^2=\dfrac{2}{3}\)
\(\Leftrightarrow...\)
Vậy ...
